前言
?熟話說得好,創新點不夠,智能優化算法來湊,不要覺得羞恥,因為不僅我們這么干,很多外國人也這么干!因為創新點實在太難想了,和優化算法結合下是最簡單的創新點了!
之前給大家分享了66個智能優化算法,更新了最近幾年發表在一區期刊的智能優化算法以及改進的優化算法。雖然有這么多個優化算法,但很多小伙伴表示還是不會用,沒有目標函數。
BP神經網絡以及智能優化算法對其初始參數的優化一直是一個熱點的話題,每年的畢設都有N多小伙伴需要這個,而這種復雜的有很多局部最優點的優化問題就是智能優化算法的一個很好的應用,那這期內容我們就分享66個智能優化算法優化BP神經網絡的代碼實現,但學會這期分享,本質上可以實現任意智能優化算法優化BP神經網絡
文末福利:拉到,有必須拿下的福利哦
數據集
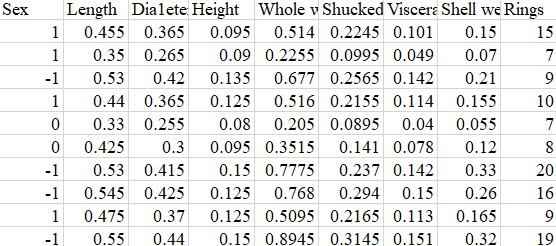
用經典鮑魚數據集為例,最后Rings是需要預測的即鮑魚的年齡,用性別(1:雄性,M;0:中性l ;?-1:雌性,F)和一些體征如長度、高度、重量等進行預測。因變量是鮑魚的年齡,有多個自變量,是一個典型多元回歸問題。
鮑魚數據形式如下:
?

目標函數
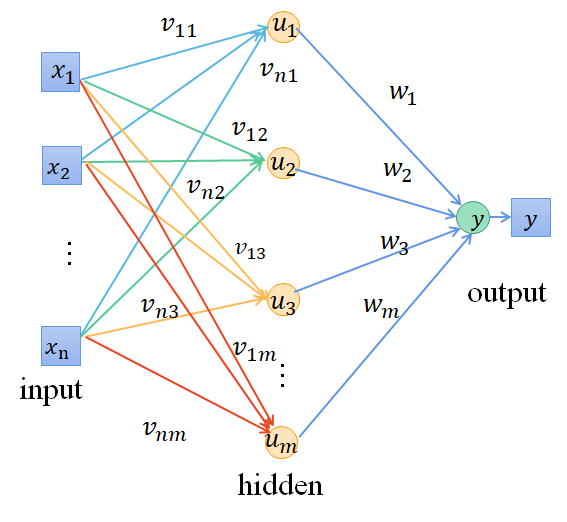
? ?對于一個固定結構的神經網絡,即神經網絡層數、神經元個數以及激活函數都一樣的情況下,可以通過優化網絡結構的初始參數來優化整個網絡的參數和結構。
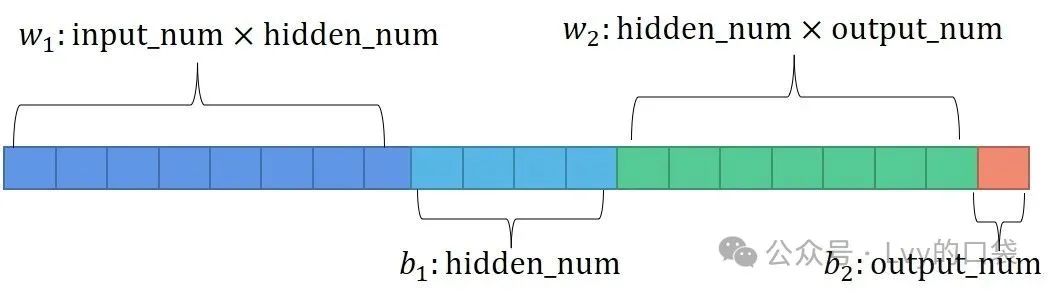
? 把優化的參數拉平成一條進行優化,優化參數的維度和網絡結構有關,我們的優化目標就是優化出一個初始網絡結構超參數,能讓網絡正向傳播得到的預測值和真實值最接近。因此我們通用的目標函數可以設置如下:
function fitness_value =objfun(input_pop)global input_num hidden_num output_num input_data output_dataw1=input_pop(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=input_pop(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=input_pop(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=input_pop(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值W1=reshape(w1,hidden_num,input_num);W2=reshape(w2,output_num,hidden_num);B1=reshape(B1,hidden_num,1);B2=reshape(B2,output_num,1);[~,n]=size(input_data);A1=logsig(W1*input_data+repmat(B1,1,n)); %需與main函數中激活函數相同A2=purelin(W2*A1+repmat(B2,1,n)); %需與main函數中激活函數相同error=sumsqr(output_data-A2);fitness_value=error; %誤差即為適應度end

數據集劃分與超參數設置
clc;clear; close all;load('abalone_data.mat')%鮑魚數據global input_num hidden_num output_num input_data output_data train_num test_num x_train_mu y_train_mu x_train_sigma y_train_sigma%% 導入數據%設置訓練數據和測試數據[m,n]=size(data);train_num=round(0.8*m); %自變量test_num=m-train_num;x_train_data=data(1:train_num,1:n-1);y_train_data=data(1:train_num,n);%測試數據x_test_data=data(train_num+1:end,1:n-1);y_test_data=data(train_num+1:end,n);%% 標準化[x_train_regular,x_train_mu,x_train_sigma] = zscore(x_train_data);[y_train_regular,y_train_mu,y_train_sigma]= zscore(y_train_data);x_train_regular=x_train_regular';y_train_regular=y_train_regular';input_data=x_train_regular;output_data=y_train_regular;input_num=size(x_train_regular,1); %輸入特征個數hidden_num=6; %隱藏層神經元個數output_num=size(y_train_regular,1); %輸出特征個數num_all=input_num*hidden_num+hidden_num+hidden_num*output_num+output_num;%網絡總參數,只含一層隱藏層;%%%自變量的個數即為網絡連接權重以及偏置popmax=1.5; %自變量即網絡權重和偏置的上限popmin=-1.5; %自變量即網絡權重和偏置的下限SearchAgents_no=50; % Number of search agents 搜索麻雀數量Max_iteration=300; % Maximum numbef of iterations 最大迭代次數% Load details of the selected benchmark function

超參數的優化和最終結果的獲取
以下展示了,使用智能優化算法優化超參數前后的使用方法,在初始超參數優化完畢后,直接把結果帶入到神經網絡中,再進行反向傳播的訓練,
%%fobj=@objfun;Time_compare=[]; %算法的運行時間比較Fival_compare=[]; %算法的最終目標比較Fival_compare1=[]; %優化過后的初始參數經過反向傳播的優化Fival_compare2=[];curve_compare=[]; %算法的過程函數比較name_all=[]; %算法的名稱記錄dim=num_all;lb=popmin;ub=popmax;pop_num=SearchAgents_no;Max_iter=Max_iteration;%% 不進行優化,隨機賦值iter=1;bestX=lb+(ub-lb).*rand(1,num_all);ER_=Fun1(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_1=Fun2(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);Fival_compare1=[Fival_compare1,ER_];Fival_compare2=[Fival_compare2,ER_1];name_all{1,iter}='NO-opti';iter=iter+1;%% 麻雀搜索算法t1=clock;[fMin_SSA,bestX_SSA,SSA_curve]=SSA(pop_num,Max_iter,lb,ub,dim,fobj); %麻雀搜索算法ER_SSA=Fun1(bestX_SSA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_SSA1=Fun2(bestX_SSA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);t2=clock;time_SSA=(t2(end)+t2(end-1)*60+t2(end-2)*3600-t1(end)-t1(end-1)*60-t1(end-2)*3600);Fival_compare=[Fival_compare,fMin_SSA];Fival_compare1=[Fival_compare1,ER_SSA];Fival_compare2=[Fival_compare2,ER_SSA1];Time_compare=[Time_compare,time_SSA(end)];curve_compare=[curve_compare;SSA_curve];name_all{1,iter}='SSA';iter=iter+1;
第一個神經網絡計算函數是MATLAB自帶的BP工具箱
function [EcRMSE]=Fun1(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data)global input_num output_num x_train_mu y_train_mu x_train_sigma y_train_sigmabestchrom=bestX;net=newff(x_train_regular,y_train_regular,hidden_num,{'logsig','purelin'},'trainlm');w1=bestchrom(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值net.iw{1,1}=reshape(w1,hidden_num,input_num);net.lw{2,1}=reshape(w2,output_num,hidden_num);net.b{1}=reshape(B1,hidden_num,1);net.b{2}=reshape(B2,output_num,1);net.trainParam.epochs=200; %最大迭代次數net.trainParam.lr=0.1; %學習率net.trainParam.goal=0.00001;[net,~]=train(net,x_train_regular,y_train_regular);%將輸入數據歸一化test_num=size(x_test_data,1);x_test_regular = (x_test_data-repmat(x_train_mu,test_num,1))./repmat(x_train_sigma,test_num,1);%放入到網絡輸出數據y_test_regular=sim(net,x_test_regular');%將得到的數據反歸一化得到預測數據test_out_std=y_test_regular;%反歸一化SSA_BP_predict=test_out_std*y_train_sigma+y_train_mu;errors_nn=sum(abs(SSA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));% disp(EcRMSE)end
第二個神經網絡計算函數是小編自己寫的BP函數???????
function [EcRMSE]=Fun2(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data)global input_num output_num x_train_mu y_train_mu x_train_sigma y_train_sigmatrain_num=length(y_train_regular); %自變量test_num=length(y_test_data);bestchrom=bestX;% net=newff(x_train_regular,y_train_regular,hidden_num,{'tansig','purelin'},'trainlm');w1=bestchrom(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值x_train_std=x_train_regular;y_train_std=y_train_regular;%vij = reshape(w1,hidden_num,input_num) ;%輸入和隱藏層的權重theta_u = reshape(B1,hidden_num,1);%輸入與隱藏層之間的閾值Wj = reshape(w2,output_num,hidden_num);%%輸出和隱藏層的權重theta_y =reshape(B2,output_num,1);%輸出與隱藏層之間的閾值%learn_rate = 0.0001;%學習率Epochs_max = 10000;%最大迭代次數error_rate = 0.1;%目標誤差Obj_save = zeros(1,Epochs_max);%損失函數% 訓練網絡epoch_num=0;while epoch_num <Epochs_maxepoch_num=epoch_num+1;y_pre_std_u=vij * x_train_std + repmat(theta_u, 1, train_num);y_pre_std_u1 = logsig(y_pre_std_u);y_pre_std_y = Wj * y_pre_std_u1 + repmat(theta_y, 1, train_num);y_pre_std_y1=y_pre_std_y;obj = y_pre_std_y1-y_train_std ;Ems = sumsqr(obj);Obj_save(epoch_num) = Ems;if Ems < error_ratebreak;end%梯度下降%輸出采用rule函數,隱藏層采用sigomd激活函數c_wj= 2*(y_pre_std_y1-y_train_std)* y_pre_std_u1';c_theta_y=2*(y_pre_std_y1-y_train_std)*ones(train_num, 1);c_vij=Wj'* 2*(y_pre_std_y1-y_train_std).*(y_pre_std_u1).*(1-y_pre_std_u1)* x_train_std';c_theta_u=Wj'* 2*(y_pre_std_y1-y_train_std).*(y_pre_std_u1).*(1-y_pre_std_u1)* ones(train_num, 1);Wj=Wj-learn_rate*c_wj;theta_y=theta_y-learn_rate*c_theta_y;vij=vij- learn_rate*c_vij;theta_u=theta_u-learn_rate*c_theta_u;end%x_test_regular = (x_test_data-repmat(x_train_mu,test_num,1))./repmat(x_train_sigma,test_num,1);% x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);%放入到網絡輸出數據x_test_std=x_test_regular';test_put = logsig(vij * x_test_std + repmat(theta_u, 1, test_num));test_out_std = Wj * test_put + repmat(theta_y, 1, test_num);%反歸一化SSA_BP_predict=test_out_std*y_train_sigma+y_train_mu;errors_nn=sum(abs(SSA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));disp(EcRMSE)end
得到不同優化函數優化BP神經網絡的適應度曲線如下
? ?將初始參數帶入到BP網絡模型中,反向傳播訓練可以得到BP工具箱優化的結果以及自己寫的網絡結果,兩者效果相差不太大
?
以下是兩種實現方式的對比

運行多次記錄結果????
? ? 不可否認的是,因為智能優化算法的存在,每次優化是有一定的隨機性的,因此我們可以多次運行取均值和方差去衡量總體的結果???????
clc;clear; close all;load('data_test1.mat')global input_num hidden_num output_num input_data output_data train_num test_num x_train_mu y_train_mu x_train_sigma y_train_sigma%% 循環5次記錄結果 訓練集和測試集隨機%% 導入數據%設置訓練數據和測試數據NUM=5; %隨機測試數for NN=1:NUM[m,n]=size(data);train_num=round(0.8*m); %自變量randlabel=randperm(m); %隨機標簽test_num=m-train_num;x_train_data=data(randlabel(1:train_num),1:n-1);y_train_data=data(randlabel(1:train_num),n);%測試數據x_test_data=data(randlabel(train_num+1:end),1:n-1);y_test_data=data(randlabel(train_num+1:end),n);% x_train_data=x_train_data';% y_train_data=y_train_data';% x_test_data=x_test_data';%% 標準化[x_train_regular,x_train_mu,x_train_sigma] = zscore(x_train_data);[y_train_regular,y_train_mu,y_train_sigma]= zscore(y_train_data);x_train_regular=x_train_regular';y_train_regular=y_train_regular';input_data=x_train_regular;output_data=y_train_regular;input_num=size(x_train_regular,1); %輸入特征個數hidden_num=6; %隱藏層神經元個數output_num=size(y_train_regular,1); %輸出特征個數num_all=input_num*hidden_num+hidden_num+hidden_num*output_num+output_num;%網絡總參數,只含一層隱藏層;%自變量的個數即為網絡連接權重以及偏置popmax=1.5; %自變量即網絡權重和偏置的上限popmin=-1.5; %自變量即網絡權重和偏置的下限SearchAgents_no=50; % Number of search agents 搜索麻雀數量Max_iteration=300; % Maximum numbef of iterations 最大迭代次數% Load details of the selected benchmark function%%fobj=@objfun;Time_compare=[]; %算法的運行時間比較Fival_compare=[]; %算法的最終目標比較Fival_compare1=[]; %優化過后的初始參數經過反向傳播的優化Fival_compare2=[];curve_compare=[]; %算法的過程函數比較name_all=[]; %算法的名稱記錄dim=num_all;lb=popmax*ones(1,dim);ub=popmin*ones(1,dim);pop_num=SearchAgents_no;Max_iter=Max_iteration;%% 不進行優化,隨機賦值iter=1;bestX=lb+(ub-lb).*rand(1,num_all);ER_=Fun1(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_1=Fun2(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);Fival_compare1=[Fival_compare1,ER_];Fival_compare2=[Fival_compare2,ER_1];name_all{1,iter}='ON-opti';iter=iter+1;%%% [ER_1,WW]=Fun2(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);% % [fMin_SSA,bestX_SSA,SSA_curve]=SSA2(pop_num,pop_or,Max_iter,lb,ub,dim,fobj);% % ER2=fun3(bestX_SSA,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data);% pop_num11=500;% [fMin_SSA,bestX_SSA1,SSA_curve]=SSA2(pop_num11,WW,Max_iter,lb,ub,dim,fobj);% ER_2=fun3(bestX_SSA1,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data);% Fival_compare1=[Fival_compare1,ER_2];% Fival_compare2=[Fival_compare2,ER_2];% name_all{1,iter}='BP-SSA';% iter=iter+1;%% 改進麻雀搜索算法t1=clock;[fMin_SSA,bestX_SSA,SSA_curve]=G_SSA(pop_num,Max_iter,lb,ub,dim,fobj); %麻雀搜索算法ER_SSA=Fun1(bestX_SSA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_SSA1=Fun2(bestX_SSA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);t2=clock;time_SSA=(t2(end)+t2(end-1)*60+t2(end-2)*3600-t1(end)-t1(end-1)*60-t1(end-2)*3600);ER_SSA2=fun3(bestX_SSA,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data); %不進行BP反向Fival_compare=[Fival_compare,ER_SSA2];Fival_compare1=[Fival_compare1,ER_SSA];Fival_compare2=[Fival_compare2,ER_SSA1];Time_compare=[Time_compare,time_SSA(end)];curve_compare=[curve_compare;SSA_curve];name_all{1,iter}='G-SSA';iter=iter+1;%%%改進鯨魚優化算法t1=clock;[fMin_EWOA,bestX_EWOA,EWOA_curve]=BKA(pop_num,Max_iter,lb,ub,dim,fobj);ER_EWOA=Fun1(bestX_EWOA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_EWOA1=Fun2(bestX_EWOA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);t2=clock;time_EWOA=(t2(end)+t2(end-1)*60+t2(end-2)*3600-t1(end)-t1(end-1)*60-t1(end-2)*3600);ER_EWOA2=fun3(bestX_EWOA,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data); %不進行BP反向Fival_compare=[Fival_compare,ER_EWOA2];Fival_compare1=[Fival_compare1,ER_EWOA];Fival_compare2=[Fival_compare2,ER_EWOA1];Time_compare=[Time_compare,time_EWOA(end)];curve_compare=[curve_compare;EWOA_curve];name_all{1,iter}='BKA';iter=iter+1;%%%正弦余弦優化算法 Sine Cosine Algorithmt1=clock;[fMin_SCA,bestX_SCA,SCA_curve]=SCA(pop_num,Max_iter,lb,ub,dim,fobj);ER_SCA=Fun1(bestX_SCA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_SCA1=Fun2(bestX_SCA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);t2=clock;time_SCA=(t2(end)+t2(end-1)*60+t2(end-2)*3600-t1(end)-t1(end-1)*60-t1(end-2)*3600);ER_SCA2=fun3(bestX_EWOA,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data); %不進行BP反向Fival_compare=[Fival_compare,ER_SCA2];Fival_compare1=[Fival_compare1,ER_SCA];Fival_compare2=[Fival_compare2,ER_SCA1];Time_compare=[Time_compare,time_SCA(end)];curve_compare=[curve_compare;SCA_curve];name_all{1,iter}='SCA';iter=iter+1;%%%POA%IGOA%IGWOt1=clock;[fMin_SCA,bestX_SCA,SCA_curve]=G_DBO(pop_num,Max_iter,lb,ub,dim,fobj);ER_SCA=Fun1(bestX_SCA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);ER_SCA1=Fun2(bestX_SCA,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data);t2=clock;ER_SCA2=fun3(bestX_EWOA,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data); %不進行BP反向time_SCA=(t2(end)+t2(end-1)*60+t2(end-2)*3600-t1(end)-t1(end-1)*60-t1(end-2)*3600);Fival_compare=[Fival_compare,ER_SCA2];Fival_compare1=[Fival_compare1,ER_SCA];Fival_compare2=[Fival_compare2,ER_SCA1];Time_compare=[Time_compare,time_SCA(end)];curve_compare=[curve_compare;SCA_curve];name_all{1,iter}='G-DBO';iter=iter+1;FFival_compare1(NN,:)=Fival_compare1;FFival_compare2(NN,:)=Fival_compare2;end%%load('color_list.mat')figure(3)color=color_list(randperm(length(color_list)),:);width=0.7; %柱狀圖寬度for i=1:length(Fival_compare1)set(bar(i,Fival_compare1(i),width),'FaceColor',color(i,:),'EdgeColor',[0,0,0],'LineWidth',2)hold on%在柱狀圖 x,y 基礎上 繪制誤差 ,low為下誤差,high為上誤差,LineStyle 誤差圖樣式,'Color' 誤差圖顏色% 'LineWidth', 線寬,'CapSize',誤差標注大小% errorbar(i, y(i), low(i), high(i), 'LineStyle', 'none', 'Color', color(i+3,:), 'LineWidth', 1.5,'CapSize',18);endylabel('obj-value')ylim([min(Fival_compare1)-0.01,max(Fival_compare1)+0.01]);ax=gca;ax.XTick = 1:1:length(Fival_compare1);set(gca,'XTickLabel',name_all,"LineWidth",2);set(gca,"FontSize",12,"LineWidth",2)title('優化工具箱')%%load('color_list.mat')figure(4)color=color_list(randperm(length(color_list)),:);width=0.7; %柱狀圖寬度for i=1:length(Fival_compare2)set(bar(i,Fival_compare2(i),width),'FaceColor',color(i,:),'EdgeColor',[0,0,0],'LineWidth',2)hold on%在柱狀圖 x,y 基礎上 繪制誤差 ,low為下誤差,high為上誤差,LineStyle 誤差圖樣式,'Color' 誤差圖顏色% 'LineWidth', 線寬,'CapSize',誤差標注大小% errorbar(i, y(i), low(i), high(i), 'LineStyle', 'none', 'Color', color(i+3,:), 'LineWidth', 1.5,'CapSize',18);endylabel('obj-value')ylim([min(Fival_compare2)-0.01,max(Fival_compare2)+0.01]);ax=gca;ax.XTick = 1:1:length(Fival_compare2);set(gca,'XTickLabel',name_all,"LineWidth",2);set(gca,"FontSize",12,"LineWidth",2)title('自寫網絡')%%figure(5)bar([Fival_compare1;Fival_compare2]')ylabel('obj-value')ylim([min(Fival_compare2)-0.01,max(Fival_compare2)+0.01]);ax=gca;ax.XTick = 1:1:length(Fival_compare2);set(gca,'XTickLabel',name_all,"LineWidth",2);set(gca,"FontSize",12,"LineWidth",2)legend('工具箱','自寫網絡')%%figure(7)color=[0.741176470588235,0.729411764705882,0.725490196078431;0.525490196078431,...0.623529411764706,0.752941176470588;0.631372549019608,0.803921568627451,...0.835294117647059;0.588235294117647,0.576470588235294,0.576470588235294;...0.0745098039215686,0.407843137254902,0.607843137254902;0.454901960784314,...0.737254901960784,0.776470588235294;0.0156862745098039,0.0196078431372549,0.0156862745098039];% 顏色1mean_compare1=mean(FFival_compare1);std1_compare1=std(FFival_compare1);mean_compare2=mean(FFival_compare2);std1_compare2=std(FFival_compare2);b=bar([mean_compare1;mean_compare2]');data=[mean_compare1;mean_compare2]';hold onerro_data=[std1_compare1;std1_compare1]';ax = gca;for i = 1 : 2x_data(:, i) = b(i).XEndPoints';endfor i=1:2errorbar(x_data(:,i),data(:,i),erro_data(:,i),'LineStyle', 'none','Color',color(i+3,:) ,'LineWidth', 2,'CapSize',18)endfor i =1:2b(i).FaceColor = color(i,:);b(i).EdgeColor= color(i+3,:);b(i).LineWidth=1.5;endylabel('obj-value')maxl=max([mean_compare1,mean_compare2]);minl=min([mean_compare1,mean_compare2]);ylim([minl-0.01,maxl+0.01]);ax=gca;ax.XTick = 1:1:length(Fival_compare2);set(gca,'XTickLabel',name_all,"LineWidth",2);set(gca,"FontSize",12,"LineWidth",2)legend('工具箱','自寫網絡')box off% net=newff(x_train_regular,y_train_regular,hidden_num,{'logsig','purelin'},'trainlm','deviderand');%%% function fitness_value =objfun(input_pop,input_num,hidden_num,output_num,input_data,output_data)function fitness_value =objfun(input_pop)global input_num hidden_num output_num input_data output_dataw1=input_pop(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=input_pop(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=input_pop(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=input_pop(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值W1=reshape(w1,hidden_num,input_num);W2=reshape(w2,output_num,hidden_num);B1=reshape(B1,hidden_num,1);B2=reshape(B2,output_num,1);[~,n]=size(input_data);A1=logsig(W1*input_data+repmat(B1,1,n)); %需與main函數中激活函數相同A2=purelin(W2*A1+repmat(B2,1,n)); %需與main函數中激活函數相同error=sumsqr(output_data-A2);fitness_value=error; %誤差即為適應度end%%function EcRMSE =fun3(input_pop,x_test_data,x_train_mu,x_train_sigma,y_train_mu,y_train_sigma,y_test_data)global input_num hidden_num output_numw1=input_pop(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=input_pop(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=input_pop(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=input_pop(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值% W1=reshape(w1,hidden_num,input_num);% W2=reshape(w2,output_num,hidden_num);% B1=reshape(B1,hidden_num,1);% B2=reshape(B2,output_num,1);vij = reshape(w1,hidden_num,input_num) ;%輸入和隱藏層的權重theta_u = reshape(B1,hidden_num,1);%輸入與隱藏層之間的閾值Wj = reshape(w2,output_num,hidden_num);%%輸出和隱藏層的權重theta_y =reshape(B2,output_num,1);%輸出與隱藏層之間的閾值% [~,n]=size(input_data);% A1=logsig(W1*input_data+repmat(B1,1,n)); %需與main函數中激活函數相同% A2=purelin(W2*A1+repmat(B2,1,n)); %需與main函數中激活函數相同% error=sumsqr(output_data-A2);% fitness_value=error; %誤差即為適應度test_num=size(x_test_data,1);x_test_regular = (x_test_data-repmat(x_train_mu,test_num,1))./repmat(x_train_sigma,test_num,1);% x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);%放入到網絡輸出數據x_test_std=x_test_regular';test_put = logsig(vij * x_test_std + repmat(theta_u, 1, test_num));test_out_std = Wj * test_put + repmat(theta_y, 1, test_num);%反歸一化SSA_BP_predict=test_out_std*y_train_sigma+y_train_mu;errors_nn=sum(abs(SSA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));% disp(EcRMSE)end%%function [EcRMSE,net1]=Fun1(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data)global input_num output_num x_train_mu y_train_mu x_train_sigma y_train_sigmabestchrom=bestX;net=newff(x_train_regular,y_train_regular,hidden_num,{'logsig','purelin'},'trainlm');w1=bestchrom(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值net.iw{1,1}=reshape(w1,hidden_num,input_num);net.lw{2,1}=reshape(w2,output_num,hidden_num);net.b{1}=reshape(B1,hidden_num,1);net.b{2}=reshape(B2,output_num,1);net.trainParam.epochs=200; %最大迭代次數net.trainParam.lr=0.1; %學習率net.trainParam.goal=0.00001;[net,~]=train(net,x_train_regular,y_train_regular);%將輸入數據歸一化test_num=size(x_test_data,1);x_test_regular = (x_test_data-repmat(x_train_mu,test_num,1))./repmat(x_train_sigma,test_num,1);%放入到網絡輸出數據y_test_regular=sim(net,x_test_regular');net1=net;%將得到的數據反歸一化得到預測數據test_out_std=y_test_regular;%反歸一化SSA_BP_predict=test_out_std*y_train_sigma+y_train_mu;errors_nn=sum(abs(SSA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));disp(EcRMSE)end%%function [EcRMSE,WW]=Fun2(bestX,x_train_regular,y_train_regular,hidden_num,x_test_data,y_test_data)global input_num output_num x_train_mu y_train_mu x_train_sigma y_train_sigmatrain_num=length(y_train_regular); %自變量test_num=length(y_test_data);bestchrom=bestX;% net=newff(x_train_regular,y_train_regular,hidden_num,{'tansig','purelin'},'trainlm');w1=bestchrom(1:input_num*hidden_num); %輸入和隱藏層之間的權重參數B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隱藏層神經元的偏置w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num); %隱藏層和輸出層之間的偏置B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...hidden_num+hidden_num*output_num+output_num); %輸出層神經元的偏置%網絡權值賦值x_train_std=x_train_regular;y_train_std=y_train_regular;%vij = reshape(w1,hidden_num,input_num) ;%輸入和隱藏層的權重theta_u = reshape(B1,hidden_num,1);%輸入與隱藏層之間的閾值Wj = reshape(w2,output_num,hidden_num);%%輸出和隱藏層的權重theta_y =reshape(B2,output_num,1);%輸出與隱藏層之間的閾值%learn_rate = 0.0001;%學習率Epochs_max = 30000;%最大迭代次數error_rate = 0.001;%目標誤差Obj_save = zeros(1,Epochs_max);%損失函數% 訓練網絡epoch_num=0;while epoch_num <Epochs_maxepoch_num=epoch_num+1;y_pre_std_u=vij * x_train_std + repmat(theta_u, 1, train_num);y_pre_std_u1 = logsig(y_pre_std_u);y_pre_std_y = Wj * y_pre_std_u1 + repmat(theta_y, 1, train_num);y_pre_std_y1=y_pre_std_y;obj = y_pre_std_y1-y_train_std ;Ems = sumsqr(obj);Obj_save(epoch_num) = Ems;if Ems < error_ratebreak;end%梯度下降%輸出采用rule函數,隱藏層采用sigomd激活函數c_wj= 2*(y_pre_std_y1-y_train_std)* y_pre_std_u1';c_theta_y=2*(y_pre_std_y1-y_train_std)*ones(train_num, 1);c_vij=Wj'* 2*(y_pre_std_y1-y_train_std).*(y_pre_std_u1).*(1-y_pre_std_u1)* x_train_std';c_theta_u=Wj'* 2*(y_pre_std_y1-y_train_std).*(y_pre_std_u1).*(1-y_pre_std_u1)* ones(train_num, 1);Wj=Wj-learn_rate*c_wj;theta_y=theta_y-learn_rate*c_theta_y;vij=vij- learn_rate*c_vij;theta_u=theta_u-learn_rate*c_theta_u;endWW=[vij(:);theta_u;Wj(:);theta_y];% W1=[Wj(:),theta_y,vij(:),theta_u];x_test_regular = (x_test_data-repmat(x_train_mu,test_num,1))./repmat(x_train_sigma,test_num,1);% x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);%放入到網絡輸出數據x_test_std=x_test_regular';test_put = logsig(vij * x_test_std + repmat(theta_u, 1, test_num));test_out_std = Wj * test_put + repmat(theta_y, 1, test_num);%反歸一化SSA_BP_predict=test_out_std*y_train_sigma+y_train_mu;errors_nn=sum(abs(SSA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));disp(EcRMSE)end
福利:
包含:
Java、云原生、GO語音、嵌入式、Linux、物聯網、AI人工智能、python、C/C++/C#、軟件測試、網絡安全、Web前端、網頁、大數據、Android大模型多線程、JVM、Spring、MySQL、Redis、Dubbo、中間件…等最全廠牌最新視頻教程+源碼+軟件包+面試必考題和答案詳解。
福利:想要的資料全都有 ,全免費,沒有魔法和套路
————————————————————————————

關注公眾號:資源充電吧
點擊小卡片關注下,回復:學習






課程1-Opencv視覺處理之基本操作與代碼詳解)






)






