1、基于淺層神經網絡的數據擬合的簡介、原理以及matlab實現
1)內容說明
基于淺層神經網絡的數據擬合是一種常見的機器學習方法,用于通過輸入數據來擬合一個非線性函數。這種方法通常包括一個輸入層、一個或多個隱藏層和一個輸出層。神經網絡通過學習權重參數來逐步優化模型,使其能夠更好地擬合訓練數據。
神經網絡的原理是通過前向傳播將輸入數據傳遞到隱藏層和輸出層,然后通過反向傳播來更新權重參數,以減小預測誤差。在每次迭代中,通過計算損失函數的梯度來更新權重,并不斷優化模型,直到達到預定的停止條件。
在MATLAB中,可以使用神經網絡工具箱來實現基于淺層神經網絡的數據擬合。首先,需要定義網絡結構、選擇激活函數、設置訓練參數等。然后,使用訓練數據來訓練神經網絡模型,并利用測試數據來評估模型的性能。
總的來說,基于淺層神經網絡的數據擬合是一種強大的機器學習方法,可以用于解決回歸、分類等問題。通過不斷優化參數,神經網絡可以更好地擬合數據,提高預測準確性。
2)算法說明?
萊文貝格-馬夸特算法
萊文貝格-馬夸特(Levenberg-Marquardt)算法是一種用于求解非線性最小二乘問題的優化算法。該算法結合了最速下降方法(Levenberg算法)和高斯-牛頓方法(Marquardt算法)的優點,旨在找到最小化目標函數的參數值。
在神經網絡中,萊文貝格-馬夸特算法通常用于訓練反向傳播神經網絡中的權重參數。該算法通過對神經網絡的損失函數進行最小化,使得神經網絡的輸出與實際觀測值更加接近。萊文貝格-馬夸特算法在神經網絡訓練過程中具有較快的收斂速度和較好的穩定性。
萊文貝格-馬夸特算法的基本思想是通過不斷地調整參數的值,使得目標函數的值逐漸減小。該算法結合了梯度下降和牛頓法的優點,可以更快地收斂到最優解,并對參數的初始值不敏感。在每一步迭代中,萊文貝格-馬夸特算法會根據當前的參數值計算一個近似的海森矩陣,然后通過調整步長來更新參數值,直到達到最優解或收斂到一個局部極小值。
總體來說,萊文貝格-馬夸特算法是一種強大且高效的優化算法,特別適用于解決非線性最小二乘問題,如神經網絡權重訓練中的參數優化。通過使用萊文貝格-馬夸特算法,可以加快神經網絡的訓練速度并提高性能,從而更好地擬合和預測數據。
貝葉斯正則化
貝葉斯正則化是一種基于貝葉斯統計理論的參數估計方法,用于處理參數估計中的過擬合問題。在機器學習和統計建模中,經常會遇到模型過于復雜,導致在訓練數據上表現良好但在測試數據上泛化能力不足的情況,這就是過擬合。貝葉斯正則化通過引入先驗概率對參數進行約束,降低模型的復雜度,從而提高模型的泛化能力。
在貝葉斯正則化中,參數估計的過程是一個加權考慮數據擬合和先驗信息的過程。貝葉斯正則化采用貝葉斯推斷的方法,通過最大化后驗概率來獲得參數的估計值。在構建模型時,需要為參數引入一個先驗概率分布,表示對參數的先驗知識或假設,然后通過貝葉斯定理將先驗信息與觀測數據結合,得到參數的后驗分布,進而進行參數估計。
一種常見的貝葉斯正則化技術是貝葉斯嶺回歸(Bayesian Ridge Regression),其中使用嶺回歸的L2范數作為先驗概率,通過最大化后驗概率來求解參數。貝葉斯嶺回歸可以在保持模型簡單性的同時提高模型的泛化能力,有效地解決過擬合問題。
總的來說,貝葉斯正則化是一種有助于解決過擬合問題的參數估計方法,通過引入先驗概率對參數進行約束,提高模型的泛化能力。貝葉斯正則化在機器學習和統計建模中得到廣泛應用,幫助提高模型的性能和魯棒性。
量化共軛梯度
量化共軛梯度(Quantum Gradient Descent)是一種基于量子計算和梯度下降結合的優化算法。量子計算是利用量子力學原理進行信息處理和計算操作的新型計算模式,其中量子比特的特性可以實現高效的并行計算和處理。
在量子共軛梯度算法中,梯度下降的更新步驟會結合經典的梯度信息和量子計算的優勢,實現更高效的優化過程。通過利用量子比特的疊加態和量子糾纏的性質,在每一步迭代中可以進行更加復雜和高效的計算運算,從而加速收斂速度和提高優化結果的精度。
量子共軛梯度算法的核心思想是利用量子計算的優勢來加速梯度下降算法的收斂過程,從而在解決大規模問題和高維度數據時提供更好的性能。該算法結合了經典梯度下降算法和量子計算的優勢,可以在一定程度上實現比傳統梯度下降算法更快的優化速度。
需要注意的是,量子共軛梯度算法目前處于研究階段,仍然需要進一步的實踐和發展以驗證其在不同領域的有效性和實用性。隨著量子計算技術的不斷發展和進步,量化共軛梯度算法有望在未來成為優化問題中的重要工具之一。
?2、加載數據
1)說明
將預測變量 bodyfatInputs 和響應變量 bodyfatTargets 加載到工作區
將體脂預測變量加載到數組 x 中,將體脂響應變量加載到數組 t 中。
2)代碼
%將預測變量 bodyfatInputs 和響應變量 bodyfatTargets 加載到工作區
load bodyfat_dataset
%將體脂預測變量加載到數組 x 中,將體脂響應變量加載到數組 t 中。
[x,t] = bodyfat_dataset;3、選擇訓練算法
1)說明
使用默認的萊文貝格-馬夸特算法 (trainlm) 進行訓練。
也可將網絡訓練函數設置為貝葉斯正則化 (trainbr) 或量化共軛梯度 (trainscg)
2)代碼
%使用默認的萊文貝格-馬夸特算法 (trainlm) 進行訓練。
%也可將網絡訓練函數設置為貝葉斯正則化 (trainbr) 或量化共軛梯度 (trainscg)
trainFcn = 'trainlm'; % Levenberg-Marquardt反向傳播。4、創建網絡
1)說明
用于函數擬合(或回歸)問題的默認網絡 fitnet 是一個前饋網絡,其默認 tan-sigmoid 傳遞函數在隱藏層,線性傳遞函數在輸出層。網絡有一個包含十個神經元(默認值)的隱藏層。網絡有一個輸出神經元,因為只有一個響應值與每個輸入向量關聯。
2)代碼
%用于函數擬合(或回歸)問題的默認網絡 fitnet 是一個前饋網絡,其默認 tan-sigmoid 傳遞函數在隱藏層,線性傳遞函數在輸出層。網絡有一個包含十個神經元(默認值)的隱藏層。網絡有一個輸出神經元,因為只有一個響應值與每個輸入向量關聯。
hiddenLayerSize = 10;
net = fitnet(hiddenLayerSize,trainFcn);5、劃分數據
1)說明
預測變量向量和響應向量將被隨機劃分,70% 用于訓練,15% 用于驗證,15% 用于測試
2)代碼
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;6、訓練及查看網絡
1)說明
訓練查看網絡
2)代碼
[net,tr] = train(net,x,t);
view(net)3)試圖效果
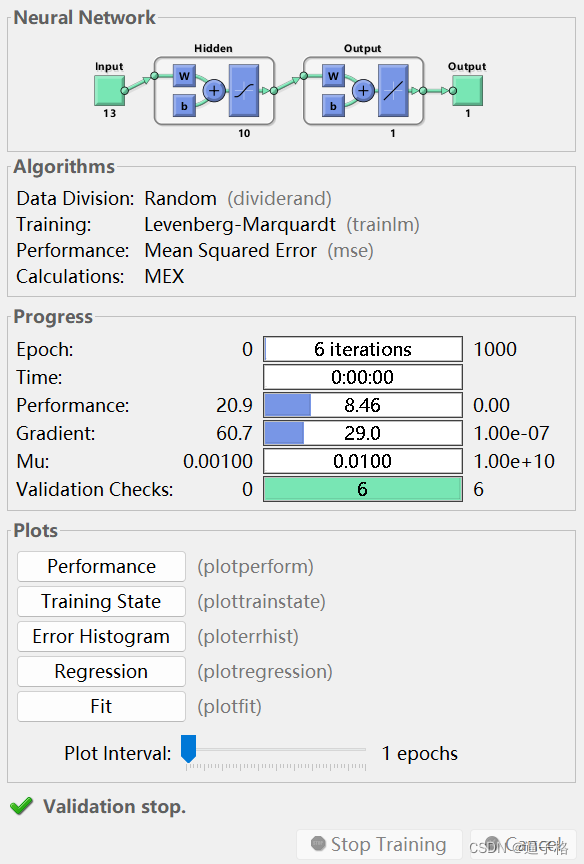
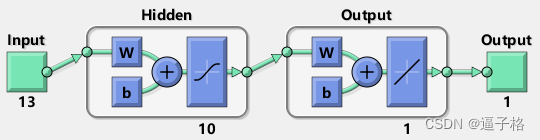 ?
?
?7、測試網絡
1)使用經過訓練的網絡來計算網絡輸出
說明:使用經過訓練的網絡來計算網絡輸出。計算網絡輸出、誤差和整體性能。
代碼
y = net(x);
e = gsubtract(t,y);
performance = perform(net,t,y)performance =19.87832)測試索引
代碼
tInd = tr.testInd;
tstOutputs = net(x(:,tInd));
tstPerform = perform(net,t(tInd),tstOutputs)tstPerform =13.12303)神經網絡數據擬合結果視圖分析
均方差圖
說明:
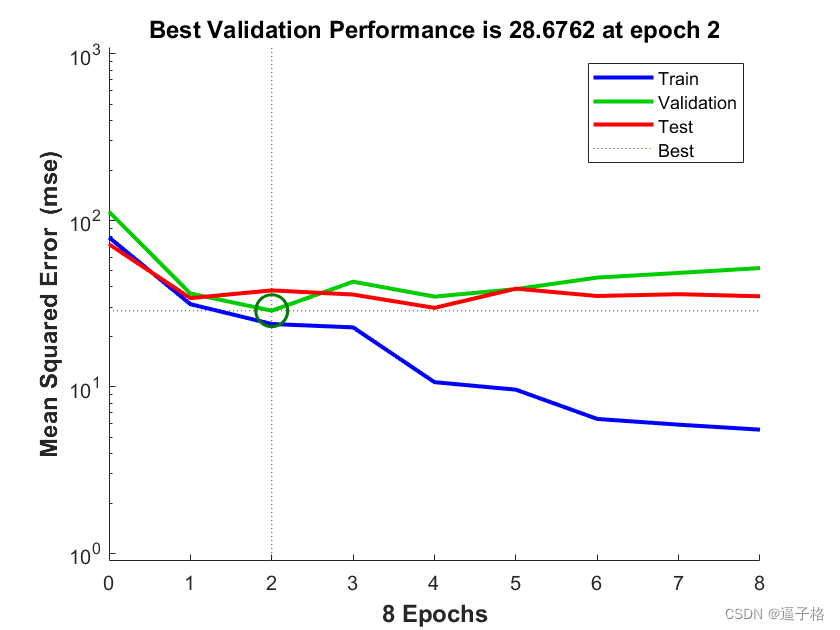
訓練狀態圖
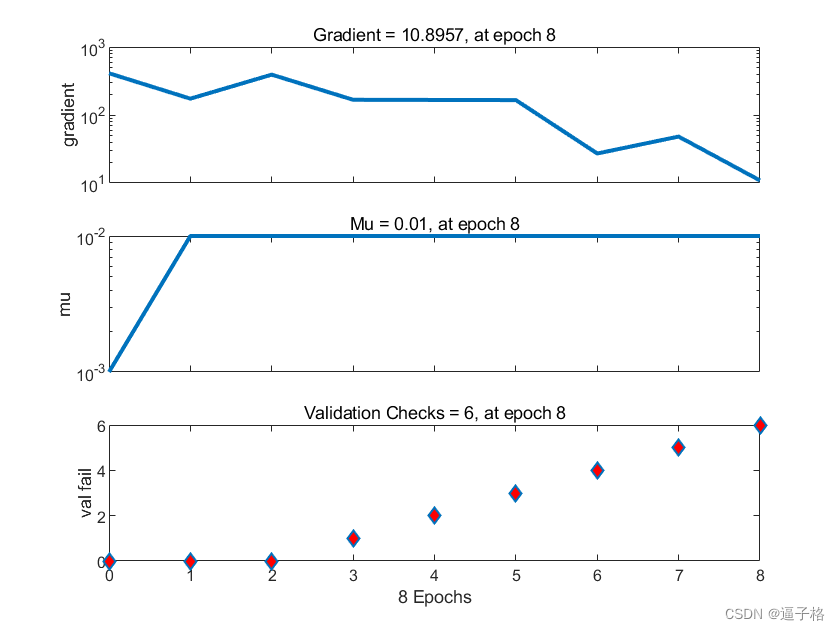
誤差分布圖
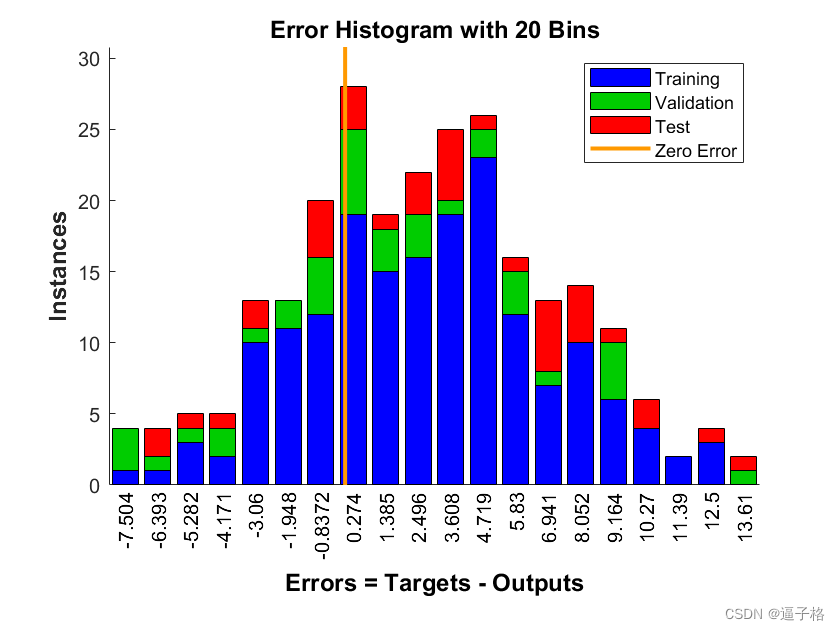
回歸圖
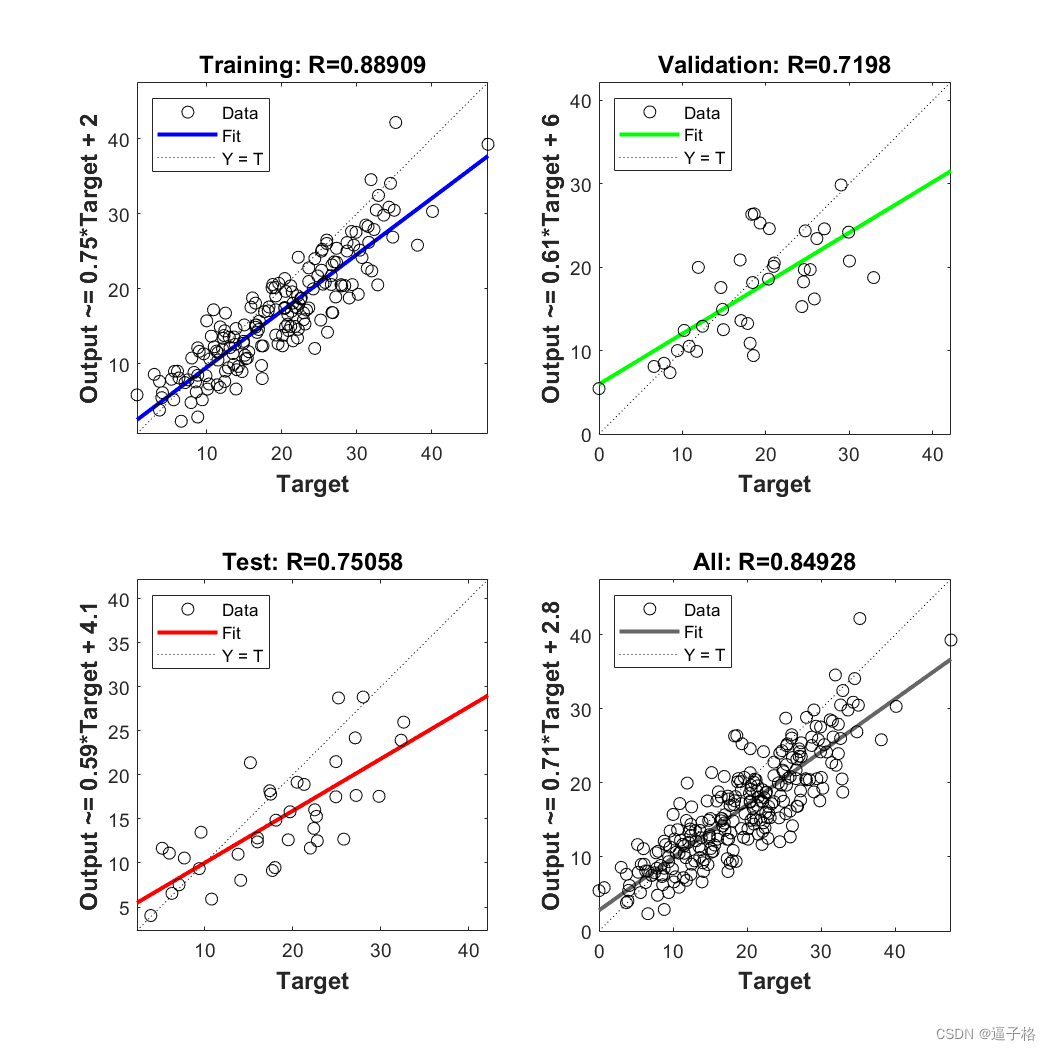
8、總結
基于淺層神經網絡的數據擬合在MATLAB中的實現主要包括以下幾個步驟:
-
數據準備:首先,需要準備訓練數據和測試數據。確保數據已經經過預處理和標準化,以便神經網絡更好地學習和擬合。
-
網絡設計:定義神經網絡的結構,包括輸入層、隱藏層和輸出層的神經元數量、激活函數等。可以選擇不同類型的網絡結構,如全連接神經網絡、卷積神經網絡等。
-
模型訓練:使用訓練數據來訓練神經網絡模型。可以選擇不同的優化算法和損失函數,如梯度下降算法和均方誤差損失函數。通過多次迭代更新權重參數,使模型能夠更好地擬合數據。
-
模型評估:使用測試數據來評估訓練好的模型的性能。可以計算預測精度、誤差率等指標,以評估模型的準確性和泛化能力。
-
參數調優:根據模型評估結果,可以對神經網絡的模型參數進行調優,如調整神經元數量、隱藏層層數、學習率等,以進一步提高模型性能。
通過以上步驟,可以使用MATLAB實現基于淺層神經網絡的數據擬合,使得模型能夠更好地學習和預測數據,從而解決各種回歸、分類等問題。神經網絡在數據擬合中的應用非常廣泛,能夠處理復雜的非線性關系,適用于各種領域的數據分析和預測任務。
9、源代碼
?代碼
%% 基于淺層神經網絡的數據擬合%% 加載數據
%將預測變量 bodyfatInputs 和響應變量 bodyfatTargets 加載到工作區
load bodyfat_dataset
%將體脂預測變量加載到數組 x 中,將體脂響應變量加載到數組 t 中。
[x,t] = bodyfat_dataset;
%% 選擇訓練算法
%使用默認的萊文貝格-馬夸特算法 (trainlm) 進行訓練。
%也可將網絡訓練函數設置為貝葉斯正則化 (trainbr) 或量化共軛梯度 (trainscg)
trainFcn = 'trainlm'; % Levenberg-Marquardt反向傳播。
%% 創建網絡
%用于函數擬合(或回歸)問題的默認網絡 fitnet 是一個前饋網絡,其默認 tan-sigmoid 傳遞函數在隱藏層,線性傳遞函數在輸出層。網絡有一個包含十個神經元(默認值)的隱藏層。網絡有一個輸出神經元,因為只有一個響應值與每個輸入向量關聯。
hiddenLayerSize = 10;
net = fitnet(hiddenLayerSize,trainFcn);
%% 劃分數據
%預測變量向量和響應向量將被隨機劃分,70% 用于訓練,15% 用于驗證,15% 用于測試
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
%% 訓練及查看網絡
[net,tr] = train(net,x,t);
view(net)
%% 測試網絡
%使用經過訓練的網絡來計算網絡輸出。計算網絡輸出、誤差和整體性能。
y = net(x);
e = gsubtract(t,y);
performance = perform(net,t,y)
%測試索引
tInd = tr.testInd;
tstOutputs = net(x(:,tInd));
tstPerform = perform(net,t(tInd),tstOutputs)?
?









)









