前言

????????在之前的文章介紹了定點數為什么需要舍入和幾種常見的舍入模式。今天我們再來看看另外一種舍入模式：向上取整fix。

10進制數的fix

????????fix：也叫 向0取整。它的舍入方式是數據往0的方向，舍入到最近的整數，比如1.75 fix到2，-0.25 fix到0等。以-2到1.75之間的16個數據（步長0.25）為例，它們的 fix 結果是這樣的：

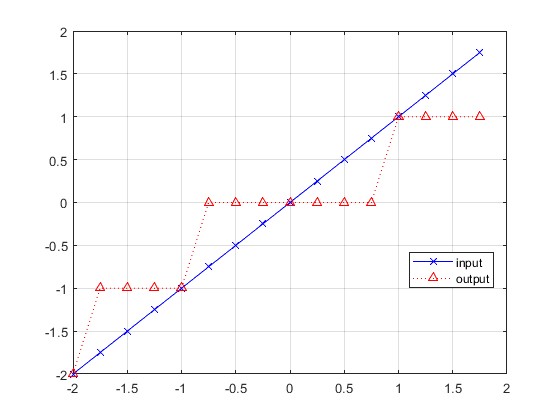
????????從上圖可以看到：

• 正數的fix，就是把小數部分（或者約定精度外的部分）丟掉。例如1.5 >> 1，0.5 >> 0，1 >> 1 等

• 負數的fix，也是把小數部分（或者約定精度外的部分）丟掉。例如-1.5 >> -1，-0.5 >> 0，-1 >> -1 等

• 0的fix，同樣是直接丟掉小數部分

2進制數的fix

????????2進制數的fix和10進制的fix類似，但是對于負數部分的處理是不同的。以Q4.2格式的定點數（字長4位，小數2位的有符號數）為例，對于負數的小數部分的處理：

• -2(d) = 10_00(b) fix后的值為 -2，等價于 10，即舍棄小數部分的值（10）

• -1.75(d) = 10_01(b) fix后的值為 -1，等價于 11，即舍棄小數部分的值（10）后再加1

• -1.5(d) = 10_10(b) fix后的值為 -1，等價于 11，即舍棄小數部分的值（10）后再加1

• -1.25(d) = 10_11(b) fix后的值為 -1，等價于 11，即舍棄小數部分的值（10）后再加1

• -1(d) = 11_00(b) fix后的值為 -1，等價于 11，即舍棄小數部分

• -0.75(d) = 11_01(b) fix后的值為 0，等價于 00，即舍棄小數部分的值（10）后再加1

• -0.5(d) = 11_10(b) fix后的值為 0，等價于 00，即舍棄小數部分的值（10）后再加1

• -0.25(d) = 11_11(b) fix后的值為 0，等價于 00，即舍棄小數部分的值（10）后再加1

????????總結一下，就是：

• 小數部分不為0時就是把小數部分（或者約定精度外的部分）丟掉再加1。

• 小數部分為0時就是把小數部分（或者約定精度外的部分）丟掉。

????????對于正數和0的處理和10進制的方式相同，都是：

直接把小數部分（或者約定精度外的部分）丟掉，例如1.25即01_01 fix的結果是1即01，0.75即00_11 fix的結果是0即00

????????從上面可以看出來，fix對于正數來說相當于向下取整floor，對于負數來說相當于向上取整ceil。因此，fix的實現可以簡化為：

首先舍去小數部分，然后剩余整數部分加上一個進位。當該數是為負的非整數時，進位為1；否則進位為0。

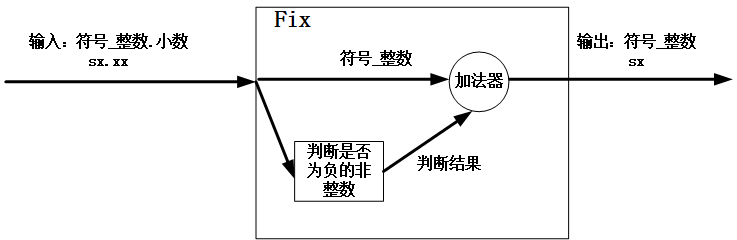
????????下面以 用fix的方式來實現Q4.2格式定點數轉Q2.0格式定點數為例，Verilog代碼如下：

module test(input   [3:0]   data_4Q2,       //有符號數，符號1位，字長4位，小數2位   output  [1:0]   data_2Q0        //有符號數，符號1位，字長2位，小數0位   
);
?
wire    carry;
?
assign  carry = data_4Q2[3] && (|data_4Q2[1:0]);    //是負數且非整數時進位為1，其他進位為0
assign  data_2Q0 = data_4Q2[3:2] + carry;           //舍棄低位（即整個小數部分）后再加進位
?
endmodule

????????因為一共只有16個數，所以我們可以用窮舉的方式來測試，TB如下：

`timescale 1ns/1ns
module test_tb();
?
reg  [3:0]  data_4Q2;           //有符號數，符號1位，整數2位，小數2位   
wire [1:0]  data_2Q0;           //有符號數，符號1位，整數2位，小數0位   integer i;                      //循環變量
?
initial begindata_4Q2 = 0;               //輸入賦初值 for(i=0;i<16;i=i+1)begin    //遍歷所有的輸入，共16個  data_4Q2 = i;                       #5; $display("data_4Q2:%h       data_2Q0:%h",data_4Q2,data_2Q0);end#20 $stop();                //結束仿真
end
?
//例化被測試模塊
test    test_inst(.data_4Q2   (data_4Q2), .data_2Q0   (data_2Q0)
);
?
endmodule

????????同時，我們也用matlab來實現同樣的功能，觀察兩者的輸出是否一致：

%--------------------------------------------------
% 關閉無關內容
clear;
close all;
clc;
?
%--------------------------------------------------
% 生成數據并做fix處理
x = -2:0.25:1.75;
F = fimath('RoundingMethod','Zero'); ? ? ? ?% 設定舍入模式為fix
data_4Q2 = fi(x,1,4,2,F); ? ? ? ? ? ? ? ? ? % 生成Q4.2格式的定點數
data_2Q0 = fi(data_4Q2,1,2,0,F); ? ? ? ? ? ?% 從Q4.2格式轉換成Q2.0格式
?
% 打印數據
for i=1:length(data_4Q2)fprintf('data_4Q2:%s ?  data_2Q0:%s\n',hex(data_4Q2(i)),hex(data_2Q0(i)))
end

????????下圖是2者分別輸出的數據（16進制），可以看到數據的輸出是一致的，證明RTL代碼無誤。

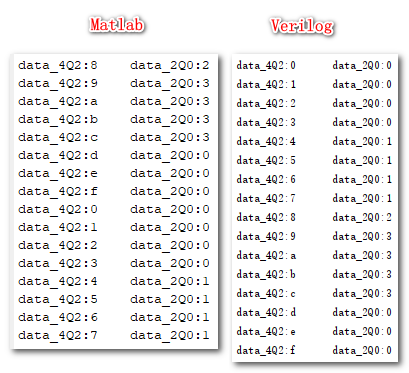
????????這幾個數的輸入分別是0101/0110/0111，即10進制數1.25/1.5/1.75，它們fix結果應該是2。從上圖來看，好像是matlab錯了，而RTL對了，但實際情況恰恰相反。現在想想結果是什么格式的？Q2.0！它能表示的最大的數是多少？是10進制的1！所以結果溢出了！

????????那為什么RTL的結果又 ”對“ 了呢？這純屬是烏龍。因為打印結果是16進制的，并不表示10進制數值，結合結果的2位位寬，可知 ”2“，實際上就是10，它是01的溢出產生的，這個數在Q2.0格式的定點數中并不表示 ”數字2“，而是數字 ”-1“。

????????matlab是有溢出處理機制的（saturate），它把溢出值把都飽和在了最大值即01（10進制的1）。為了防止這種情況的發生，我們也要設計對應的溢出處理機制。因為是向上取整，所以結果只會是正向的溢出，那么就只要限定最大值即可，把Verilog代碼改一下：

module test(input   [3:0]   data_4Q2,               //有符號數，符號1位，字長4位，小數2位   output  [1:0]   data_2Q0                //有符號數，符號1位，字長2位，小數0位   
);
?
wire            carry;
wire    [2:0]   data_temp;                  //擴展1bit，防止溢出
?
assign  carry = |data_4Q2[1:0];                                         //是整數時進位為0，非整數進位為1
assign  data_temp = {data_4Q2[3],data_4Q2[3:2]} + {2'b00,carry};        //中間變量，舍棄低位（即整個小數部分）后再加進位
assign  data_2Q0 = (data_temp[2:1]==2'b01) ? 2'b01 : data_temp[1:0];    //data_2Q0的高2位為01說明產生了正向的進位，即溢出
?
endmodule

????????非整數的ceil，相當于先丟小數部分，然后把剩余的整數部分+1：

????????定點數從Q4.2格式轉Q2.0格式是一個比較特殊的例子，因為它相當于把小數部分全部舍棄掉了，如果舍入要求不是全部小數位，而是部分小數位，那么處理方式是一樣的嗎？

????????是一樣的。對于其他情況則只需要把精度要求外的小數部分舍棄即可。例如Q5.3格式的定點數轉Q3.1格式，則只需要把最后兩位小數舍棄即可，例如：

00.111 是0.875，fix到向0方向即向下方向距離它最近的Q3.1格式的數是0.5即00.1，即00.111 >> 00.1。操作上相當于上面說的舍棄掉多余的小數位

10.111 是-1.125，fix到向0方向即向上方向距離它最近的Q3.1格式的數是-1即11.0，即10.111 >> 10.1 + 1 >> 11.0。操作上相當于上面說的舍棄掉多余的小數位，然后加1。

????????其他類似，不贅述了。