• 卡爾曼濾波器是一種有效的估計算法，主要用于在存在噪聲的環境中估計動態系統的狀態。它通過結合預測模型（系統動態）和觀測數據（包括噪聲）來實現這一點。在卡爾曼濾波中，調整過程噪聲協方差矩陣 ( Q ) 和測量噪聲協方差矩陣 ( R ) 是非常關鍵的，因為這兩個參數直接影響濾波器的性能。

  過程噪聲 ( Q )

  • 意義：( Q ) 表示對系統模型中隨機噪聲的估計。如果 ( Q ) 設置得較小，表明我們相信系統模型的精度較高，系統狀態的預測與實際值差異不大。
  • 調整策略：如果 ( Q ) 過小，濾波器對模型預測的信任度過高，可能會忽略一些實際中的動態變化，導致濾波結果跟不上實際系統的變化（系統易發散）。如果 ( Q ) 過大，濾波器對模型的信任度降低，會更多地依賴觀測數據，這可能導致濾波輸出過于嘈雜，反映了過多的測量噪聲。

  測量噪聲 ( R )

  • 意義：( R ) 表示對測量過程中噪聲的估計。較大的 ( R ) 表示對測量數據的信任度較低。
  • 調整策略：如果 ( R ) 過大，濾波器對測量數據的依賴減少，響應變慢，可能導致濾波器響應對系統變化不夠敏感。如果 ( R ) 過小，濾波器對測量數據的信任度過高，這可能使濾波結果受到測量噪聲的較大影響，導致估計值波動較大。

  調試技巧

  • 單變量調整：在調試過程中，通常建議固定一個噪聲參數（如先固定 ( R )），調整另一個（如 ( Q )），觀察濾波器的性能如何變化。這樣可以分別了解每個參數的影響。
  • 逐步調整：開始時可以將 ( Q ) 設置得較小，( R ) 設置得較大，然后逐步增加 ( Q )、減小 ( R )，觀察濾波器的穩定性和響應速度。
  • 性能指標：觀察濾波器在調整參數后的性能，如估計誤差、收斂速度、對系統變化的響應等。

  實際應用中的考量

  • 系統動態：系統的具體特性和動態變化也會影響最佳的 ( Q ) 和 ( R ) 值。例如，對于動態變化劇烈的系統，可能需要較大的 ( Q ) 來適應這種變化。
  • 噪聲特性：實際測量過程中噪聲的統計特性（如方差、頻譜）也應該在調整 ( R ) 時考慮。

  總的來說，調整 ( Q ) 和 ( R ) 是一個迭代過程，需要基于系統性能反饋和實際觀測數據來不斷優化。在實際應用中，也可以利用一些自適應算法來動態調整這些參數，以達到更好的濾波效果。

  https://yunyang1994.github.io/2021/07/10/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2%E7%AE%97%E6%B3%95-%E6%B0%B8%E8%BF%9C%E6%BB%B4%E7%A5%9E/

  魯道夫 ? 卡爾曼在一次訪問 NASA 埃姆斯研究中心時，發現他的卡爾曼濾波算法能幫助解決阿波羅計劃的軌道預測問題，最終，飛船正確駛向月球，完成了人類歷史上的第一次登月。卡爾曼因而一舉成名，后來還被美國總統奧巴馬授予了國家科學勛章。

  S-G 濾波器（Savitzky–Golay filter)，它的核心思想是對一定長度窗口內的數據點進行 k 階多項式擬合，其加權系數是通過在滑動窗口內對給定高階多項式的最小二乘擬合得出。

  import numpy as np
  import matplotlib.pyplot as plt
  from scipy.signal import savgol_filterN = 100  # 數據點的數量
  X = np.arange(N)  # 創建一個0到N-1的數組# 模擬100幀帶有噪聲的原始數據，使用正弦波和高斯噪聲
  Y1 = np.sin(np.linspace(0, np.pi*2, num=N)) + np.random.normal(0, 0.1, size=N)window_length = 5      # 滑動窗口長度，該值需為正奇整數
  poly_order = 1         # 窗口內的數據點進行k階多項式擬合，其值需要小于 window_lengthY2 = []                # 用于存儲平滑后的數據
  cache_data = []        # 緩存隊列，用于存儲當前滑動窗口內的數據for i in range(N):                       # 實時地遍歷每幀噪聲數據origin_data = Y1[i]                  # 獲取當前幀的數據cache_data.append(origin_data)       # 將當前幀數據添加到緩存隊列if i < window_length:                # 如果當前幀數小于滑動窗口長度smooth_data = origin_data        # 直接使用原始數據作為平滑數據else:window_data = np.array(cache_data)  # 將緩存隊列轉換為numpy數組window_data = savgol_filter(window_data, window_length, poly_order)  # 對滑動窗口數據進行Savitzky-Golay濾波平滑smooth_data = window_data[window_length//2]  # 取滑動窗口中間位置的數據作為平滑結果cache_data.pop(0)                            # 將緩存隊列的最早數據移除，保持窗口大小不變Y2.append(smooth_data)  # 將平滑結果添加到結果列表中

觀察這個過程，發現有個非常嚴重的 bug：被平滑的數據需要依賴前幾幀，也就是說 S-G 濾波具有一定的滯后性，比如說如果 window_size = 5，那么就會滯后 2 幀。而卡爾曼濾波可以較好地解決這個問題的痛點，它只要獲知上一時刻狀態的估計值以及當前狀態的觀測值就可以計算出當前狀態的估計值，因此不需要記錄觀測或者估計的歷史信息

上述方程是卡爾曼濾波五個方程之一，名為狀態更新 State Update Equation。其含義為：

因此，狀態更新方程為:

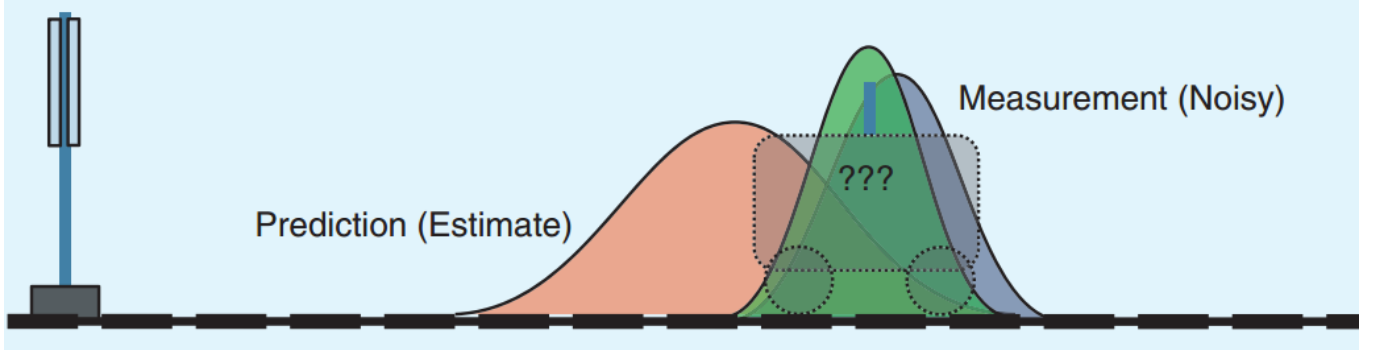
兩種方法都有一定的可信度。那能否將兩種答案相融合呢，卡爾曼濾波就是做了這樣的事情。**如下圖所示，假設兩種方法的誤差都滿足正態分布，如下圖所示。如果正態分布越尖銳陡峭，則說明這種方法的預測結果越可信；如果越緩和平坦，則說明越不可信。**為了融合這兩種方法的預測結果，我們給這兩種分布分別賦予一個權重，該權重代表了這個分布對融合結果的重要性。經過融合后的分布變得比之前兩種分布更加尖銳，這表明結果更加可信了。

方差是權重，融合結果更接近方差小的

那么如何給出一個合理的權重分布呢，這就是卡爾曼濾波要做的事情。

卡爾曼濾波模型

Kalman 濾波分為 2 個步驟**，預測(predict)和校正(correct)。**

預測是基于上一時刻狀態估計當前時刻狀態，

校正則是綜合當前時刻的估計狀態與觀測狀態，估計出最優的狀態。

**預測階段負責根據前一時刻的狀態估計值來推算當前時刻的狀態變量先驗估計值和誤差協方差先驗估計值；校正階段負責將先驗估計和新的測量變量相融合改進的后驗估計。**卡爾曼濾波算法是一個遞歸的預測—校正方法，即只要獲知上一時刻狀態的估計值以及當前狀態的觀測值就可以計算出當前狀態的估計值，因此不需要記錄觀測或者估計的歷史信息。

從上面的五個公式中，我們發現：其實卡爾曼濾波的每次迭代更新就是為了求出卡爾曼增益 K，因為它代表了融合估計值和測量值之間的權重。下面這個視頻很好地講解如何通過最小化誤差協方差矩陣求出 K：、

https://www.bilibili.com/video/BV1hC4y1b7K7/?t=565.857338&spm_id_from=333.1350.jump_directly&vd_source=8272bd48fee17396a4a1746c256ab0ae

Python 代碼實現

在上面過程中，只有 PQRK 四個矩陣還尚未確定。顯然增益矩陣 K 是不需要初始化的，P 是誤差矩陣，初始化可以是一個隨機的矩陣或者 0，只要經過幾次的處理基本上就能調整到正常的水平，因此也就只會影響前面幾次的濾波結果。

• Q：預測狀態協方差，越小系統越容易收斂，我們對模型預測的值信任度越高；但是太小則容易發散，如果 Q 為零，那么我們只相信預測值；Q 值越大我們對于預測的信任度就越低，而對測量值的信任度就變高；如果 Q 值無窮大，那么我們只信任測量值；
• R：觀測狀態協方差，如果 R 太大，則表現它對新測量值的信任度降低而更愿意相信預測值，從而使得 kalman 的濾波結果會表現得比較規整和平滑，但是其響應速度會變慢而出現滯后；
• P：誤差協方差初始值，表示我們對當前預測狀態的信任度。它越小說明我們越相信當前預測狀態；它的值決定了初始收斂速度，一般開始設一個較小的值以便于獲取較快的收斂速度。隨著卡爾曼濾波的迭代，P的值會不斷的改變，當系統進入穩態之后P值會收斂成一個最小的估計方差矩陣，這個時候的卡爾曼增益也是最優的，所以這個值只是影響初始收斂速度。

假設系統的真實狀態是一條正弦曲線，我們在測量過程中伴隨一定正態分布的隨機噪聲，使用 python 模擬該過程如下：

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 8)  # 設置圖形的顯示大小# 初始化參數
n_iter = 500  # 迭代次數
sz = (n_iter,)  # 數組的大小x = np.sin(np.linspace(0, np.pi*2, num=n_iter)) # 測量值，使用正弦函數生成
z = np.sin(np.linspace(0, np.pi*2, num=n_iter)) + np.random.normal(0, 0.1, size=n_iter) # 真實值，正弦值加上噪聲plt.figure()  # 創建一個圖形
plt.plot(z,'k+',label='noisy measurements')  # 繪制噪聲測量數據
plt.plot(x,color='g',label='truth value')  # 繪制真實值
plt.legend()  # 顯示圖例
plt.show()  # 顯示圖形

接下來我們使用卡爾曼濾波對這段噪聲進行實時去燥和平滑處理：

# 為數組分配空間
xhat=np.zeros(sz)      # 后驗估計值
P=np.zeros(sz)         # 后驗誤差估計
xhatminus=np.zeros(sz) # 先驗估計值
Pminus=np.zeros(sz)    # 先驗誤差估計
K=np.zeros(sz)         # 增益或融合因子# 超參數設定，實測調整
R = 0.1**2              # 觀測噪聲的方差
Q = 1e-4                # 過程噪聲的方差# 初始猜測
xhat[0] = 0.0
P[0] = 1.0for k in range(1, n_iter):# 預測階段xhatminus[k] = xhat[k-1] # 根據前一個后驗估計值預測當前值Pminus[k] = P[k-1] + Q   # 更新預測誤差的協方差# 更新階段K[k] = Pminus[k] / (Pminus[k] + R)  # 計算卡爾曼增益xhat[k] = xhatminus[k] + K[k] * (z[k] - xhatminus[k]) # 根據觀測更新當前估計P[k] = (1 - K[k]) * Pminus[k]        # 更新誤差協方差plt.plot(z, 'k+', label='noisy measurements')         # 繪制噪聲測量值
plt.plot(x, color='g', label='truth value')           # 繪制真實值
plt.plot(xhat, 'b-', label='a posteri estimate')      # 繪制后驗估計值
plt.legend()                                          # 顯示圖例
plt.show()                                            # 顯示圖形

貝葉斯定理（原理）

https://www.liaoxuefeng.com/article/1565255725482019

貝葉斯定理的核心思想就是不斷根據新的證據，將先驗概率調整為后驗概率，使之更接近客觀事實。

在貝葉斯公式中，各個部分的定義如下：

貝葉斯公式通常寫作：
[
$$P(A|B)=\frac{P(B|A)\times P(A)}{P(B)}$$
]

其中：

• ( P(A|B) ) 是 后驗概率（Posterior Probability）：在觀察到事件 ( B ) 之后，事件 ( A ) 發生的概率。
• ( P(B|A) ) 是 似然概率（Likelihood）：已知事件 ( A ) 發生時，觀察到事件 ( B ) 的概率。
• ( P(A) ) 是 先驗概率（Prior Probability）：在觀察到事件 ( B ) 之前，事件 ( A ) 發生的概率。
• ( P(B) ) 是 邊際概率（Marginal Probability） 或 標準化常數（Normalizing Constant）：事件 ( B ) 發生的總概率，無論事件 ( A ) 是否發生。

在貝葉斯理論中，后驗概率 ( $P(A|B)$ ) 是我們最關心的，因為它提供了考慮了新證據后事件 ( $A$ ) 的更新概率。先驗概率 ( $P(A)$ ) 表示在獲得新的數據或證據之前對事件 ( $A$ ) 發生概率的假設或估計。