論文筆記

資料

1.代碼地址

https://github.com/BIT-DA/RoTTA

2.論文地址

https://arxiv.org/abs/2303.13899

3.數據集地址

coming soon

1論文摘要的翻譯

測試時間自適應(TTA)旨在使預先7訓練的模型適用于僅具有未標記測試數據流的測試分布。大多數以前的TTA方法已經在簡單的測試數據流上取得了很大的成功，例如來自單個或多個分布的獨立采樣數據。然而，在自動駕駛等現實世界應用的動態場景中，這些嘗試可能會失敗，其中環境逐漸變化，測試數據隨著時間的推移進行相關采樣。在這項工作中，我們探索了這樣的實際測試數據流來動態部署該模型，即實際測試時間適應(PTTA)。為此，針對PTTA中復雜的數據流，提出了一種健壯的測試時間適配(ROTTA)方法。更具體地說，我們提出了一種穩健的批歸一化方案來估計歸一化統計量。同時，在考慮時效性和不確定性的基礎上，利用內存庫對類別平衡數據進行采樣。此外，為了穩定訓練過程，我們開發了一種教師-學生模型的時間感知重權策略。大量的實驗證明，ROTTA算法能夠在相關采樣數據流上實現連續的測試時間自適應。我們的方法易于實現，是快速部署的一個很好的選擇。

1 介紹

面對不斷變化的分布，隨著誤差梯度的累積，偽標記法或 熵最小值法等傳統算法變得更加不可靠。此外，測試樣本之間的高度相關性導致了對批量歸一化統計量的錯誤估計和模型的崩潰。在這種分析的驅動下，適應這樣的數據流將會遇到兩大障礙
1)批次歸一化統計中的錯誤估計導致測試樣本的錯誤預測，從而導致無效的適應；
2)模型很容易或很快地對相關抽樣造成的分布過度擬合。因此，這種動態情景迫切需要一種新的TTA范式來實現穩健的適應。
我們推出了一個更現實的TTA設置，在測試階段，分布變化和相關采樣同時發生。我們稱這種實用的測試時間適應，或簡稱為PTTA。為了更清楚地了解PTTA和以前的設置之間的異同，我們在圖1中將它們可視化，并在表1中進行總結。

本方法實現的大致思路：

• 首先用指數移動平均維護的全局統計來替換當前批次的錯誤統計。它在BatchNorm層中估計統計量是一種更穩定的方式。
• 考慮buffered樣本的時效性和不確定性的情況下，用類別平衡抽樣模擬了一批內存中的類獨立數據。較新且不太確定的樣本以更高的優先級保存在內存中。有了這批類別均衡、及時、有信心的樣本，我們就可以獲得當前分布的快照。
• 我們引入了一種時間感知的重加權策略，該策略考慮了記憶庫中樣本的時效性，并利用師生模型進行了穩健的自適應。

2論文的創新點

• 提出了一種新的更適合實際應用的測試時間自適應機制，即實際測試時間自適應(PTTA)。PTTA既考慮了分布變化，又考慮了相關抽樣。
• 我們在PTTA中對現有方法的性能進行了基準測試，發現它們只考慮了問題的一個方面，導致了無效的適應。
  *我們提出了一種健壯的測試時間自適應方法(ROTTA)，它更全面地考慮了PTTA挑戰。實施的簡便性和有效性使其成為一個實用的部署選項。
• 我們在常見的TTA基準，即CIFAR-10-C和CIFAR-100C以及大規模DomainNet數據集上廣泛展示了PTTA的實用性和ROTTA的有效性。ROTA獲得了最先進的結果，大大超過了最佳基準(分別將CIFAR-10-C、CIFAR-100-C和DomainNet的平均分類錯誤分別減少了5.9%、5.5%和2.2%)。

3 Robust Test-Time Adaptation方法的概述

3.1 問題定義

給定在源域$DS=\{(Xs，Ys)\}$上預先訓練的參數為${\theta }_0$的模型$f_{{\theta }_0}$，所提出的實用測試時間自適應旨在使$f_{{\theta }_0}$適應在線未標記樣本流$X_0，X_1，...，X_t$，其中$X_t$是分布$P_{test}$中隨時間t連續變化的一批高度相關的樣本。更具體地說，在模型測試的時候，隨著時間的推移，測試分布$P_{test}$作為$P_0，P_1，\dots ，P_{\infty }$連續變化。在時間步長$t$，我們將收到一批未標記和相關的樣本來自$P_{test}$的$X_t$。接下來，將$X_t$輸入到模型$f_{{\theta }_t}$中，并且該模型需要使其自身適應當前的測試數據流并動態地調整$f_{{\theta }_t}(X_t)$。
事實上，這種設置在很大程度上是由動態場景中部署模型的實際需求驅動的。以§1中提到的自動駕駛為例，測試樣本高度相關，數據分布隨著天氣或位置的變化而不斷變化。另一個例子是智能監控的情況，相機會在一定的時間連續捕捉到更多的人，比如下班后，但在工作時間會越來越少。同時，白天和晚上的光照條件也在不斷變化。
部署的模型應該在這樣的動態場景中穩健地進行調整。總之，在現實世界中，分布變化和數據關聯往往是同時發生的。因此，現有的TTA方法在從這樣的動態場景中采樣測試流時可能會變得不穩定。

ROTTA的概述如圖2所示。

3.2Robust Test-Time Adaptation 描述

Robust batch normalization (RBN)

批歸一化（batch normalization，BN）是一種廣泛使用的訓練技術，它可以加快網絡的訓練和收斂速度，并通過降低梯度爆炸和消失的風險來穩定訓練過程。在訓練時，給定特征圖$F\in {\mathbb{R}}^{B\times C\times H\times W}$作為BN層的輸入，按通道方式計算平均$\mu \in {\mathbb{R}}^C$和方差${\sigma }^2\in {\mathbb{R}}^C$如下：$$\begin{gathered} {\mu }_c=\frac{1}{BHW}\sum _{b=1}^B\sum _{h=1}^H\sum _{w=1}^W{F}_{(b,c,h,w)},\text{(1)} \\ {\sigma }_c^2=\frac{1}{BHW}\sum _{b=1}^B\sum _{h=1}^H\sum _{w=1}^W{\left(F_{(b,c,h,w)}?{\mu }_c\right)}^2.\text{(2)} \end{gathered}$$
然后，以通道方式標準化和細化特征圖，如下所示
$$BN(F_{(b,c,h,w)};\mu ,{\sigma }^2)={\gamma }_c\frac{F_{(b,c,h,w)}?{\mu }_c}{\sqrt{{\sigma }_c^2+?}}+{\beta }_c,(3)$$
其中$\gamma ，\beta \in {\mathbb{R}}^c$是層中的可學習參數，$?>0$，是數值穩定性的常量。同時，在訓練過程中，BN層維護一組全局運行均值和運行方差$({\mu }_s，{\sigma }_s^2)$以供推理。
由于測試時會發生域間數據shift，導致全局統計量$({\mu }_s，{\sigma }_s^2)$對測試特征歸一化不準確，導致性能顯著下降。為了解決上述問題，一些方法使用當前批次的統計數據進行歸一化。不幸的是，當測試樣本在PTTA設置下具有很高的相關性時，當前批次的統計信息也無法正確地規格化特征映射，如圖c所示。具體地說，BN的性能隨著數據相關性的增加而迅速降低。

基于以上分析，我們提出了一種穩健的批歸一化模塊，該模塊維護一組全局統計量$({\mu }_g，{\sigma }_g^2)$來穩健地歸一化特征映射。在整個測試時間自適應之前，$({\mu }_g，{\sigma }_g^2)$被初始化為預訓練模型的運行均值和方差$({\mu }_s，{\sigma }_s^2)$。在調整模型時，我們首先用指數移動平均來更新全局統計量，即：$$\begin{gathered} {\mu }_g=(1?\alpha ){\mu }_g+\alpha \mu ,\text{(4)} \\ {\sigma }_g^2=(1?\alpha ){\sigma }_g^2+\alpha {\sigma }^2,\text{(5)} \end{gathered}$$，(5)其中$(\mu ，{\sigma }^2)$是memory bank中buffer samples的統計。然后我們將特征歸一化并仿射為等式(3)配合$({\mu }_g，{\sigma }_g^2)$。在對測試樣本進行推斷時，我們直接使用$({\mu }_g，{\sigma }_g^2)$來計算輸出公式為Eq(3)。雖然簡單，但RBN足夠有效地解決了PTTA測試流上的歸一化問題。

3.2.2 Category-balanced sampling with timeliness and uncer-tainty (CSTU).

在PTTA設置中，時間$t$時候的測試樣本$X_t$之間的相關性導致觀察到的分布${\hat{\mathcal{P}}}_{test}$和測試分布${\mathcal{P}}_{test}$之間的偏差。具體地說，邊緣標簽分布$p(y|t)$往往不同于$p(Y)$。隨著時間$t$的推移，隨著$X_t$的不斷學習，可能會導致模型適應不可靠的分布${\hat{\mathcal{P}}}_{test}$，從而導致無效的適應和增加模型崩潰的風險。
為了解決這個問題，我們提出了一種容量為$N$的類別平衡memory bank $M$，該存儲庫在更新時考慮了樣本的及時性和不確定性。特別是，我們采用測試樣本的預測作為偽標簽來指導$M$的更新。同時，為了保證類別之間的平衡，我們將$M$的容量平均分配給每個類別，并首先替換主要類別的樣本(參見算法1中的第5-9行)。此外，由于測試分布的不斷變化，模型中的舊樣本價值有限，甚至可能削弱模型適應當前分布的能力。此外，正如所建議的那樣，高不確定性的樣本總是產生錯誤的梯度信息，這可能會阻礙模型適應。
考慮到這一點，我們將M中的每個樣本附加一組啟發式$(\mathcal{A},\mathcal{U})$，其中$\mathcal{A}$被初始化為0，并隨著時間$t$增加，$\mathcal{A}$是樣本的存在的時間，$\mathcal{U}$是作為預測的熵計算的不確定性。接下來，我們結合及時性和不確定性來計算一個啟發式分數，即帶有及時性和不確定性的類別平衡抽樣，如下：$$\mathcal{H}={\lambda }_t\frac{1}{1+\exp (?\mathcal{A}/\mathcal{N})}+{\lambda }_u\frac{\mathcal{U}}{\log \mathcal{C}},(6)$$，(6)其中${\lambda }_t和{\lambda }_u$權衡了實時性和不確定性，為了簡單起見，所有實驗的${\lambda }_t和{\lambda }_u$都設置為1.0。$C$是類別的數量。
我們在算法1中總結了我們的抽樣算法。使用CSTU，我們可以獲得當前測試分布${\mathcal{P}}_{test}$的健壯快照，并有效地使模型適應于它。

3.2.3 Robust training with timeliness.

實際上，在用我們的RBN替換BN層并獲得CSTU抽樣選擇的memory bank后，我們可以直接采用廣泛使用的偽標簽或熵最小化技術來進行測試時間適配。然而，我們注意到，太舊或不可靠的實例仍然有機會留在M中，因為保持類別平衡是重中之重。此外，過于激進的模型更新會使不可靠的類別平衡，導致不穩定的適應。同時，分布變化引起的誤差累積也使得上述方法不可行。
為了進一步降低來自舊的和不可靠的實例的誤差梯度信息的風險并穩定自適應，我們使用穩健的無監督學習方法，提出了teacher-student模型，并提出了時效性重加權策略。此外，為了時間效率和穩定性，在自適應過程中只訓練RBN中的仿射參數。
在時間步$t$時，在用教師模型$f_{{\theta }_t^T}$推斷相關數據$X_t$并用$X_t$更新Memory bank M之后，我們開始更新學生模型$f_{{\theta }_t^S}$和教師模型$f_{{\theta }_t^T}$。首先，我們通過最小化以下損失來更新學生模型${\theta }_t^S$→${\theta }_{t+1}^S$的參數：
$${\mathcal{L}}_r=\frac{1}{\Omega }\sum _{i=1}^{\Omega }\mathcal{L}(x_i^{\mathcal{M}},{\mathcal{A}}_i;{\theta }_t^T,{\theta }_t^S),(7)$$
其中$?=|\mathcal{M}|$是內存塊的總占用量，$x_i^{\mathcal{M}}$和$A_i(i=1，...，?)$分別是內存庫中的實例及其使用時長。隨后，通過指數移動平均將教師模型更新為
$${\theta }_{t+1}^T=(1?\nu ){\theta }_t^T+\nu {\theta }_{t+1}^S.,(8)$$
為了從內存庫中計算實例$x_i^{\mathcal{M}}$的損失值，時效性重新加權項計算如下
$$E({\mathcal{A}}_i)=\frac{\exp (?{\mathcal{A}}_i/\mathcal{N})}{1+\exp (?{\mathcal{A}}_i/\mathcal{N})},(9)$$
其中$A_i$是$x_i^{\mathcal{M}}$的年齡，$N$是內存庫的存儲能力。然后，我們計算來自學生模型的強增廣視點$x_i^{{}^{\prime \prime }}$的軟最大預測$P_S(y|x‘’i)$和來自教師模型的弱增廣視點x^'_i的軟最大預測PS(y|x’i)之間的交叉熵如下：
$$?(x_i^{\prime },x_i^{\prime \prime })=?\frac{1}{\mathcal{C}}\sum _{c=1}^c{p}_T(c|x_i^{\prime })\log p_S(c|x_i^{\prime \prime }).(10)$$最后，配備了公式(9)和公式(10)，公式的右側。公式(7)約化為損失$$\mathcal{L}(x_i^{\mathcal{M}},{\mathcal{A}}_i;{\theta }_t^T,{\theta }_t^S)=E({\mathcal{A}}_i)?(x_i^{\prime },x_i^{\prime \prime }).$$
綜上所述，由于配備了RBN、CSTU和具有時效性的健壯訓練，我們的ROTA能夠有效地使任何預先訓練的模型適應動態場景。

4 論文實驗

數據集

CIFAR10-C
CIFAR100-C
DomainNet
是迄今為止用于領域適應的最大和最難處理的數據集，由345個類別的約60萬張圖像組成。它由六個不同的域組成，包括剪貼畫(CLP)、信息圖(INF)、繪畫(PNT)、快速繪制(QDR)、真實(REL)和素描(Sketch)。我們首先在六個領域中的一個領域的訓練集上預訓練源模型，并在其余五個領域的測試集上驗證所有基線方法。

補充細節

所有實驗都是在PyTorch框架下進行的。在對腐敗具有穩健性的情況下，遵循前面的方法，我們從RobustBench基準中獲得了預訓練模型，包括用于CIFAR10→CIFAR10-C的WildResnet-28和用于CIFAR100→CIFAR100-C的ResneXt-29。然后，我們逐一更改最高嚴重程度為5的測試損壞，以模擬PTTA中測試分布隨時間的連續變化。在大空隙下泛化的情況下，我們對DomainNet中的每個域通過標準分類損失來訓練ResNet-101，并不斷地使它們適應除源域之外的不同域。同時，我們利用Dirichlet分布來模擬所有數據集的相關采樣測試流。優化采用學習速率為1×10?3的ADAM優化器，1弱化為RESIZE+CenterCrop。強增強是Clip、ColorJitter和RandomAffine等九種操作的組合。β=0.9.為了進行公平的比較，我們將所有方法的批處理大小設置為，將Rotta的內存庫容量設置為N=64。關于超參數，我們在所有實驗中采用了一組統一的ROTTA值，包括α=0.001、ν=0.001、λt=1.0、λu=1.0和δ=0.1。附錄中提供了更多詳細信息。

4.1和現有方法比較

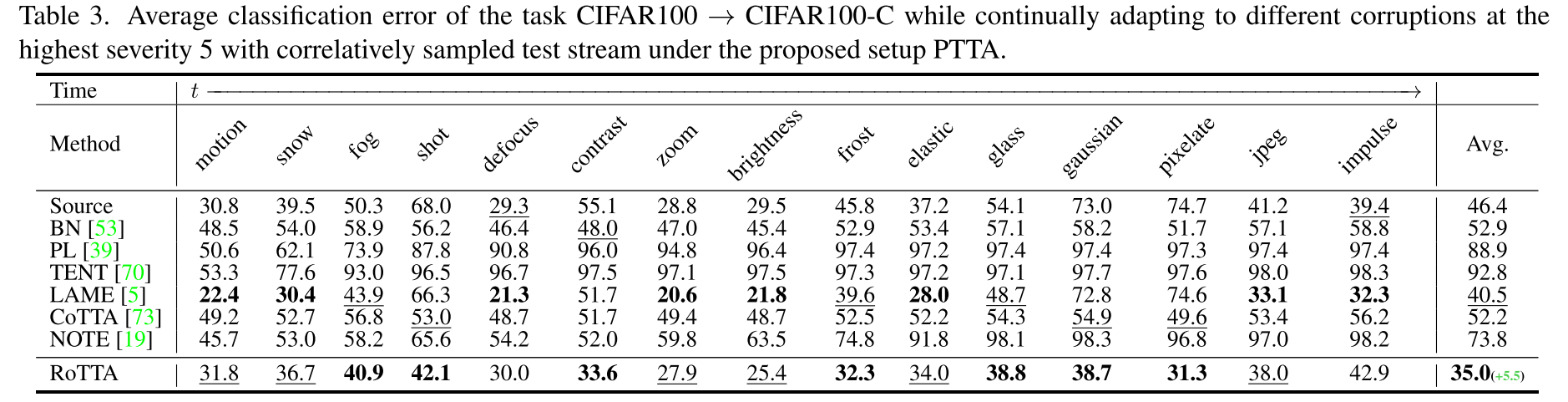
在腐敗情況下的健壯性。CIFAR10→CIFAR10-C和CIFAR100→CIFAR100-C的分類錯誤分別見表2和表3。隨著時間的推移，我們改變了當前最高嚴重性為5的腐敗類型，并同時將樣本數據關聯起來用于推理和適應。相同的測試流在所有比較的方法之間共享。從表2和表3可以看出，與以前的方法相比，ROTTA獲得了最好的性能。此外，ROTA算法比次優算法CIFAR10→CIFAR10-C和CIFAR100→CIFAR100-C分別提高了5.9%和5.5%的性能，驗證了ROTTA算法在PTTA下適應模型的有效性。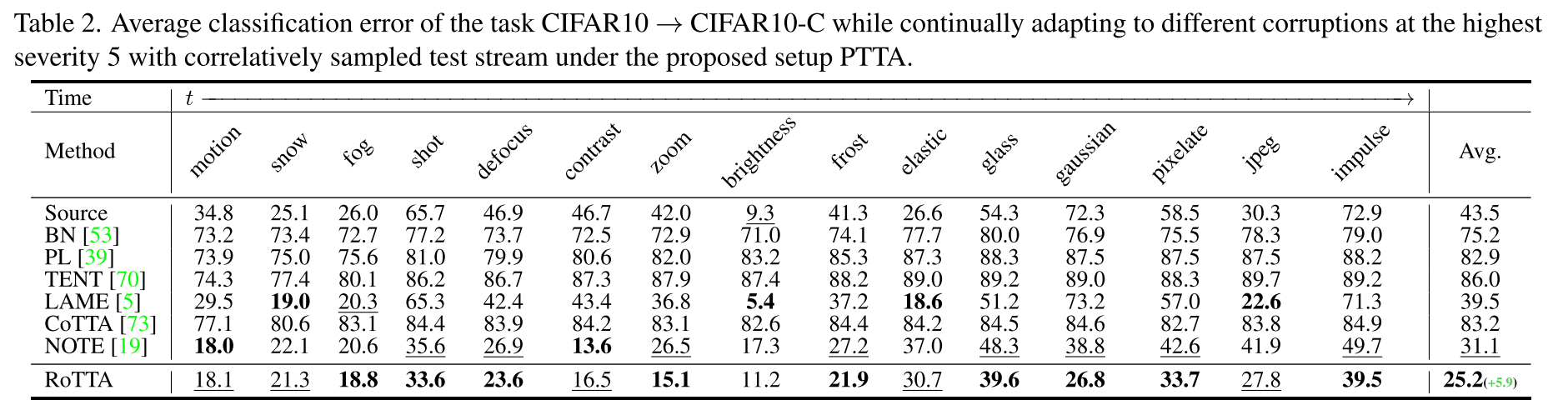

4.2消融實驗

4.2.1 Effect of each component.

(1)ROTTA w/o RBN，在TEAT[70]中用測試時間BN替換RBN；
(2)ROTTA w/o CSTU，直接在測試流上適應模型；
(3)ROTTA w/o魯棒訓練(RT)，直接調整模型，僅采用最小熵。
結果如表5所示
我們可以觀察到所有變體都出現了顯著的性能下降，證明了我們所提出的方法的每一部分對PTTA都是有效的。以一個分量為例，在沒有對特征映射進行穩健歸一化的情況下，ROTTA算法在CIFAR10-C和CIFAR100-C上的性能分別下降了50.2%和16.3%，證明了RBN具有足夠的魯棒性來解決相關采樣數據流的歸一化問題。CSTU通過維護測試分發版本的及時且可靠的快照，使ROTTA能夠適應更穩定的分發版本。同時，具有時效性的穩健訓練大大減少了錯誤的積累。在PTTA下，每個組成部分都發揮著重要的作用，以實現有效的適應。

4.2.2 Effect of the distribution changing order.

分布變化順序的影響。為了排除固定順序的分布變化的影響，我們對CIFAR10-C和CIFAR100-C分別進行了10種不同的變化序列的實驗
如圖4a和圖4b所示，無論采用何種設置，ROTA都能取得優異的效果。相關采樣測試流的詳細結果如表6所示，ROTTA在CIFAR10C和CIFAR100-C上分別取得了4.3%和4.7%的進度。這表明ROTTA可以在長期場景中穩健而有效地適應模型，其中分布不斷變化，測試流被獨立或相關地采樣，使其成為模型部署的良好選擇。

4.2.3 Effect of Dirichlet concentration parameter δ.

我們在CIFAR100-C上改變δ的值，并將ROTTA與圖4C中的其他方法進行比較。隨著δ值的增加，BN、PL、TANT和COTTA的性能迅速下降，因為它們沒有考慮測試樣本之間日益增加的相關性。注[19]對相關采樣的測試流是穩定的，但沒有考慮分布的變化，導致無效的適應。同時，測試樣本之間較高的相關性將使標簽的傳播更加準確，這就是為什么LAME的結果略有改進。最后，優異穩定的結果再次證明了ROTA的穩定性和有效性。

4.2.4 Effect of batch size.

在實際場景中，考慮到部署環境可能使用不同的測試批次大小，我們使用不同的測試批次大小值進行實驗，結果如圖4d所示。為了進行公平的比較，我們控制了ROTTA模型的更新頻率，以便反向傳播中涉及的樣本數量相同。隨著批量的增加，我們可以看到，除了LAME略有下降外，所有比較的方法都有顯著的改善。
這是因為批次中的類別數量隨著批次大小增加，導致總體相關性變得較低，但標簽的傳播變得更加困難。最重要的是，ROTTA在不同的批次大小上取得了最好的結果，再次證明了它在動態場景中的健壯性。

5總結

這項工作提出了一種更現實的TTA設置，即在測試階段同時進行分布變化和相關采樣，即實際測試時間適應(PTTA)。針對PTTA算法存在的問題，提出了一種針對復雜數據流的穩健測試時間自適應方法(ROTTA)。更具體地說，通過穩健的批歸一化來估計一組用于特征地圖歸一化的穩健統計。同時，在考慮時效性和不確定性的情況下，采用內存庫對測試分布進行分類均衡抽樣，以獲取測試分布的快照。此外，我們還提出了一種基于師生模型的時間感知重加權策略，以穩定適應過程。