目錄
1.凸分析
1.1 為什么需要凸分析
1.2 凸分析相關概念
1.3 凸規劃定義
1.4 單變量NLP凸分析?
1.5 多變量NLP凸分析
2.拉格朗日松弛
2.1 拉格朗日函數
2.2 拉格朗日對偶
2.2.1 弱對偶性?
2.2.2 凸性
2.2.3?強對偶性
2.2.4 與LP對偶關系
3.KKT條件?
3.1 KKT介紹
3.2 KKT舉例
來源:Coursera課程/Operations Research (3): Theory week5/6
課程前言:
運籌學包括三個部分:模型,算法和理論,大部分場景下,理論(theory)是關于最優性條件(optimality conditions),求解實際問題需要建立模型,求解模型需要使用算法,而理論能幫助開發更好的算法
(1)最優性條件
- 線性規劃:對偶性
- 整數規劃:全單模矩陣
- 帶約束的非線性規劃:拉格朗日和KKT條件?
博客Operations Research課程之非線性規劃(梯度下降|牛頓法|Gurobi+Python)中提到的梯度下降和牛頓法適用于無約束的非線性規劃,對于帶約束的非線性規劃問題,本文首先介紹凸規劃,然后介紹兩種工具:Lagrangian relaxation和?KKT condition
1.凸分析
1.1 為什么需要凸分析
與LP問題相比,NLP更困難
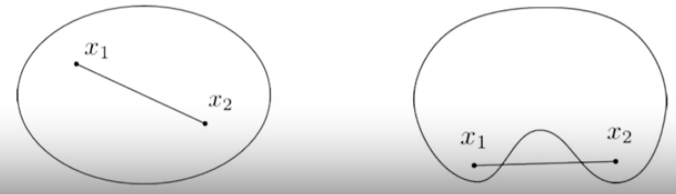
- 在NLP中,一個局部最小(最優)不總是全局最小(最優),如左圖所示,x1是局部最小但是不是全局最小
- 在有最優解NLP中,可能不存在極點最優解(extreme point),如右圖所示,最優解是(2,2)但是極點是(0,4)和(4,0)

沒有人能開發有效的算法來解決通用NLP,為了更容易求解NLP(找到一個全局最優解),我們希望NLP有以下特征:
- 我們希望局部最優就是全局最優
- 我們希望保證有極點最優解(當存在一個最優解時)
了解這些特征,就需要了解凸分析(convex analysis)?
1.2 凸分析相關概念
(1)凸集convex set
定義1(凸集convex set)
凸集中任意兩點的連線也在集合內,如左圖所示,右圖不是凸集?
(2)?凸函數convex functio
?定義2(凸函數convex function)
?凸函數有一個上升曲線,任意兩點連線上某點的取值要大于實際取值,如左圖所示,右圖不是凸函數

(3)?凹函數concave?function
?定義3(凹函數concave?function)

上面紅色框的是凸集和凸函數,其中凸函數最后一個是三維,畫圖會發現一個碗的形狀,因此是凸函數。?
(4)全局最優與局部最優
命題1(凸函數的全局最優性global optimality)
(5)極點與最優解
命題2
對任何在凸可行域上有全局最小的凹函數,全局最小是一個極點
1.3 凸規劃定義
根據上述兩個命題可知,如果想在凸可行域F上最小化函數f
- 如果函數f是凸的,就搜索一個局部最小
- 如果函數f是凹的,就搜索F中的極點
對于LP問題,有兩個重要特征

因此我們可以用貪婪搜索關注極點,從而找到最優解,這也是單純形法的思想,單純形法通過不斷搜索更好的基本可行解(極點)來尋找最優解。
定義4(凸規劃convex program CP)
如果一個NLP的可行域是凸的并且目標函數在可行域上也是凸的,那么這個NLP是CP問題
根據定義4可得命題5?
命題5
1.4 單變量NLP凸分析?
前面定義了凸性和凸規劃的概念,在給定一個函數后,我們需要知道它是不是凸的,比較簡單的函數可以通過凸函數定義來證明,但是復雜的函數是不能直接看出的,首先針對單變量NLP
單變量NLP凸分析條件
其中條件2稱為FOC(first order condition),對所有函數,FOC都是局部最優的必要條件,對于凸函數,FOC還是全局最優的充分條件。求解NLP問題,凸分析對于尋找局部最優或全局最優是非常關鍵的。以庫存控制中的EOQ經濟訂貨批量模型為例說明對于單變量NLP的凸分析過程

1.5 多變量NLP凸分析
?在Operations Research課程之非線性規劃中介紹過梯度和Hessian矩陣

對于多變量NLP,其凸性理論和單變量類似
多變量NLP凸分析條件
?有一個關鍵概念,條件1中的半正定(positive semi-definite PSD)
半正定(positive semi-definite PSD)
下面舉例說明多變量NLP凸分析及求解過程

雖然不能有效的解決通類NLP問題(general NLP),但是求解CP問題還是存在一些有效的算法,對于CP類的NLP,可以結合凸分析使用上述1.4和1.5節中的方法,如果FOC難以直接求解,還可以使用牛頓法和梯度下降,但是這些方法都只適用于無約束,接下來介紹求解帶約束的非線性凸規劃問題用到的方法:拉格朗日松弛和KKT條件
2.拉格朗日松弛
2.1 拉格朗日函數
對于帶約束的非線性規劃問題,當約束難處理時,最直觀的方法是先忽略這些約束,求解問題找到最優解,如果滿足約束就是原問題的最優解,如果不滿足約束只能尋找一個最近的可行解。很顯然這種方法有缺陷。現在換一種思路:不是直接忽略所有約束,而是允許違反約束,但是盡量保證可行性。

拉格朗日松弛將約束條件通過拉格朗日乘子結合到目標函數中,其核心是獎勵可行性(reward feasibility)和懲罰不可行(penalize infeasibility)。注意拉格朗日乘子也可以為負,但是后面表達式也要變化,只要兩者乘積能表示核心即可。下面是一個簡單的轉化例子
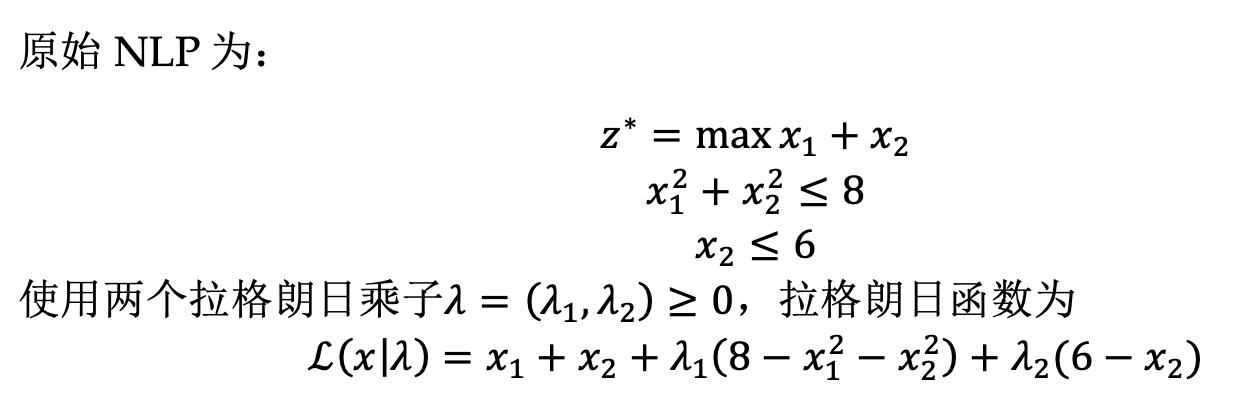
2.2 拉格朗日對偶
2.2.1 弱對偶性?
弱對偶性:拉格朗日松弛能提供原始NLP一個bound
回想LP及其對偶問題:任何可行的對偶解都能為原始LP提供一個bound,通過尋找對偶最優解能為原始LP提供最緊的bound,這和拉格朗日松弛為原始NLP提供bound類似,因此最小化拉格朗日函數也稱為拉格朗日對偶

拉格朗日對偶除了具有弱對偶性,還有一些其它需要探討的性質:
- 拉格朗日函數的凸性
- 強對偶性
- LP對偶和拉格朗日對偶的關系
2.2.2 凸性
拉格朗日對偶是凸的
無論原始NLP凸性如何,拉格朗日對偶NLP都是凸的,因此可以用數值算法比如梯度下降求解,這個關鍵性質正是拉格朗日對偶在求解帶約束非線性規劃問題的優勢
2.2.3?強對偶性
拉格朗日對偶的強對偶性
2.2.4 與LP對偶關系
LP對偶是拉格朗日對偶的一種特例
3.KKT條件?
3.1 KKT介紹
KKT條件根據三位學者命名,全稱Karush-Kuhn-Tucker conditions,用于判斷帶約束的非線性規劃的某個解是否是最優解候選,注意此處適用于滿足正則條件(regular NLP),KKT條件的證明可自尋其它資料,KKT條件使用到了2.1節拉格朗日函數的概念

KKT條件對于NLP只是必要條件,但是對CP是必要且充分條件
對于一般的非線性規劃問題,最優解一定滿足KKT,但是滿足KKT的不一定是最優解。如果這個非線性規劃問題屬于凸規劃,那么滿足KKT條件的解就是全局最優解。?
3.2 KKT舉例



在KKT條件下能幫助為帶約束的非線性規劃問題找到一些候選解,比較這些解再尋找全局最優。










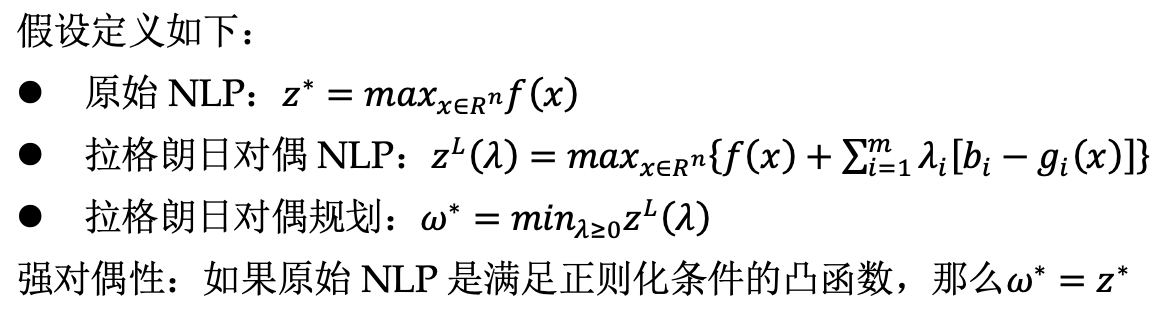

是什么?有什么用?)











)

)




