題目描述
如題,已知一個數列,你需要進行下面兩種操作:
-
將某一個數加上?𝑥x
-
求出某區間每一個數的和
輸入格式
第一行包含兩個正整數?𝑛,𝑚n,m,分別表示該數列數字的個數和操作的總個數。
第二行包含?𝑛n?個用空格分隔的整數,其中第?𝑖i?個數字表示數列第?𝑖i?項的初始值。
接下來?𝑚m?行每行包含?33?個整數,表示一個操作,具體如下:
-
1 x k?含義:將第?𝑥x?個數加上?𝑘k -
2 x y?含義:輸出區間?[𝑥,𝑦][x,y]?內每個數的和
輸出格式
輸出包含若干行整數,即為所有操作?22?的結果。
輸入輸出樣例
輸入 #1復制
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
輸出 #1復制
14 16
說明/提示
【數據范圍】
對于?30%30%?的數據,1≤𝑛≤81≤n≤8,1≤𝑚≤101≤m≤10;
對于?70%70%?的數據,1≤𝑛,𝑚≤1041≤n,m≤104;
對于?100%100%?的數據,1≤𝑛,𝑚≤5×1051≤n,m≤5×105。
數據保證對于任意時刻,𝑎a?的任意子區間(包括長度為?11?和?𝑛n?的子區間)和均在?[?231,231)[?231,231)?范圍內。
樣例說明:
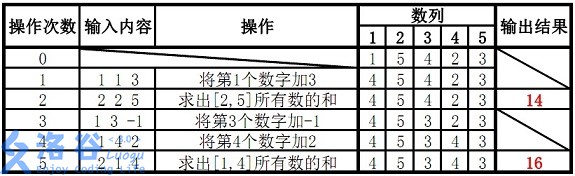
故輸出結果14、16
1.首先想到的做法
一看到區間加數和求區間段的和,本能的第一反應就是用差分和前綴和,甚至不用差分,因為它只要在一個數加1即可,只要前綴和處理,但是題目給的詢問會在某個點加了數后再求區間和,這樣就導致了每一次求區間和的時候都要去求一次前綴和這樣就導致了時間復雜度爆了,為5e5*5e5,直接導致有三個點因為超時沒法過去。有沒有不超時的辦法呢?有,就是線段樹。
2.
線段數可以做到兩種操作都為O(longN),大大減少時間復雜度。
線段數主要分為構造樹,某個點加數,求區間和。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<vector>
#include<math.h>
#include<iomanip>
#include<set>
#include<queue>
#include<stack>
#include<map>
#include<list>
#include <stdlib.h>
#include<deque>
#include <stdlib.h>
#include <time.h>
#include<cstdlib>
using namespace std;
int n, m, a[500005], f[2000005];//f為線段數
void buildtree(int k,int l,int r)//k是當前線段的編號,l到r為這一區間
{if (l == r)//到最底層{f[k] = a[l];return;}int m = (l + r) / 2;buildtree(k + k, l, m);//左子樹buildtree(k + k + 1, m + 1, r);//右子樹f[k] = f[k + k] + f[k + k + 1];//當前節點的和
}
void add(int k, int l, int r, int x, int y)//在x處加y
{f[k] = f[k] + y;//牽一發而動全身,x之上的都要加if (l == r)//葉子節點返回{return;}int m = (l + r) / 2;if (m >= x){add(k + k, l, m, x, y);}else{add(k + k + 1, m + 1, r, x, y);}
}
int getsum(int k,int l,int r,int s,int t)
{if (l == s && r == t){return f[k];}int m = (l + r) / 2;if (m >= t){return getsum(k + k, l, m,s,t);}else if (m < s){return getsum(k + k + 1, m + 1, r, s, t);}else{return getsum(k + k, l, m, s, m) + getsum(k + k + 1, m + 1, r, m+1, t);}
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}buildtree(1, 1, n);for (int i = 1; i <= m; i++){int t, x, y;cin >> t >> x >> y;if (t == 1){add(1, 1, n, x, y);}if (t == 2){cout << getsum(1, 1, n, x, y) << endl;}}
}

)















:HyperLogLog)
