目錄

一、動態規劃算法概念

?題一

1、算法解析

1）確定狀態：

?2）狀態轉移方程：

?3）初始化：

4）填表順序：

5）返回值：

2、代碼

題二

1、算法解析

1、確定狀態

2、狀態轉移方程

3、初始化

4、填表順序

5、返回值

2、代碼

3、空間優化版本

?題三

1、算法解析

1、確定狀態：

2、狀態轉移方程：

3、初始化：

4、填表順序：

5、返回值：

2、代碼

??題四

1、算法解析

1、確定狀態：

2、狀態轉移方程：

3、初始化：

4、填表順序：

5、返回值：

2、代碼

一、動態規劃算法概念

首先，什么是動態規劃？
很簡單，就是動態的規劃。呃.....
概念名不要緊，重要的是理解其算法思想，并且能夠靈活的運用其思想和方法來處理和解決現實生活中的問題，即改造世界。
動態規劃的思想，具有很強的抽象性，例如什么重復子結構、最優子結構等等，你一聽就暈了，這什么玩意？
一般來說，學校的課程教學，很學院派。通常是直接灌輸式的給你一個世界觀和方法論，然后直接讓你去屠龍。
這個是一個超越經驗的東西，直接給你了。但是，我們并不能理解這個結論，因為太抽象。
算法是一個由很多具體問題，經過長期總結歸納而形成的一個經驗過程。算法思想算法思想，為什么不是算法公式呢？這是因為無法統一，只能是思想。
需要結合很多具體的實際問題來進行，來體會，來聯系，來加深理解。
因此，在我的算法欄目中，是不會直接給你丟一堆歸納性理論的，而是，先告訴你是什么
然后再告訴你要怎么做。多做題，在這個過程中，你需要自己領悟體會。
體會什么？通過許多例題的解決過程，慢慢形成經驗的直覺，再去變通，舉一反三，而后融會貫通。
同志，共勉之。

下面我們直接上手，我會給你一個固定的，過程性解決問題的套路模板。
然后你根據這個模板，去套題目，找出相關的變量和關鍵因素。
再根據此去寫代碼。
動態規劃，一般分為5個步驟：

1、確定狀態：
剛開始一般會先畫一個dp表，再去填表，某一個位置的值就是解

這一步要做的就是：明確dp數組里面的值所表示的含義
就是 dp[i] 這個值，是什么意思？
那么，怎么定義狀表示呢？
這個要根據題目要求具體分析
一般來說，一維數組的狀態表示，有兩種：
以i為結尾，如何如何；或者以i為起點，如何如何。

2、狀態轉移方程：
狀態轉移方程就是：dp[i] 等于什么 ？
一般來說，狀態轉移方程，就是根據 dp[ i ] 之前或者 dp[ i ] 之后，來推導出 dp[ i ] 的值
只要你能根據之前或或者之后的值來推導出 dp[ i ] 的值
那么，狀態轉移方程就出來了
但是，怎么推？
這個就要就題目而言
但是，大體的思路是這樣的：根據最近的狀態來劃分問題
一般來說，dp[i] 的值，要么是前面的 dp[i-1] 或者后面的 dp[i+1]

3、初始化：
初始化就是保證，在我們進行填表的時候不越界
例如說，我要求 dp[0] / dp[1] 的值，需要前面的位置，但是此時明顯已經越界
因此，這兩個位置需要單獨處理

4、填表順序：
什么是填表順序？
很好理解，例如說
i位置值得求解，需要前面兩個位置的值已經存在才能求解
因此，也就是說在算i位置時，i-1 和 i-2 位置已經填了，已經有值了
所以，我們的填表順序應該是從前往后，因為后面的值的求解需要前面的值
反之，就是從后往前。

5、返回值：
就是看你要dp數組的哪個位置的值，
題目要去要什么值，你就根據題目給他return就好。
這個很好理解吧？

6、代碼書寫
動態規劃的代碼書寫過程是比較固定的，一般來說就分成四個步驟：
1）創建dp表
2）初始化
3）填表
4）確定返回值

7、空間優化：
空間優化就是不需要那么多空間，就可以實現目的。
怎么實現呢？
滾動數組：從左向右賦值還是從右向左賦值
這個在后面的題目中會提到。

ok，講到這里，你懂了嗎？
沒聽懂？那就對了。
下面跟著我來，很簡單，放輕松。
我會帶你把這些套路用上，去分析解決問題，跟著我的思路就好。
前面比較簡單的題目我會給的非常細致，后面逐漸粗略。

?題一

746. 使用最小花費爬樓梯 - 力扣（LeetCode）

1、算法解析

1）確定狀態：

確定狀態是在干什么？
就是確定狀態dp數組中的值代表什么含義。根據分析，我們發現：

狀態表的dp[i]值是到達該位置的最小花費

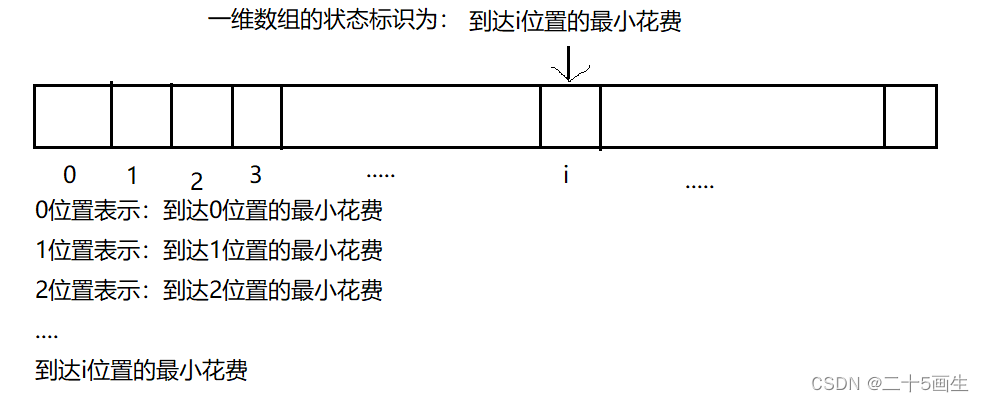
2）狀態轉移方程：

一般來說，狀態轉移方程，就是根據i位置之前或者i位置之后，來推導出i的值
只要你能根據之前或或者之后的值來推導出i的值
那么，狀態轉移方程就出來了
但是，怎么推？
這個就要就題目而言
但是，大體的思路是這樣的：根據最近的狀態來劃分問題

在這個題目中，我們第 i 位置的值，需要前面兩個位置的值來確定，其分析過程如下：

3）初始化：

初始化就是保證，在我們進行填表的時候不越界
例如說，我要求dp[0]/dp[1]位置的值，需要前面的位置，但是此時明顯已經越界
因此，這兩個位置需要單獨處理

4）填表順序：

什么是填表順序？
很好理解，例如說本題
i位置值得求解，需要前面兩個位置的值已經存在才能求解
因此，也就是說在算i位置時，i-1 和 i-2 位置已經填了，已經有值了
所以，在這個題中，我們的填表順序應該是從前往后，因為后面的值的求解需要前面的值

5）返回值：

因為我們要的是跨過所有臺階，所以這里的返回值是一維數組第n個位置的值
因此，返回值即dp[n]

2、代碼

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//創建dp表（我們要返回n位置，多創建一個位置）int n = cost.size();vector<int> dp(n+1);//初始化（走到0和走到1，是不需要花費的）dp[0] = 0;dp[1] = 0;//填表  for(int i = 2; i<=n; ++i){dp[i] = min((dp[i-1] + cost[i-1]), (dp[i-2] + cost[ i-2 ]));}//確定返回值return dp[n];}
};

題二

1137. 第 N 個泰波那契數 - 力扣（LeetCode）

1、算法解析

你自己根據我第一題的過程，自己照著求解一般，然后寫出代碼。

1、確定狀態

確定狀態是在干什么？
就是確定狀態dp數組中的值代表什么含義
dp表里某個位置值的狀態就是題目的解

2、狀態轉移方程

dp[i] = dp[i-1] + dp[i-2] + ap[i-3];題目都直接給了

3、初始化

保證填表的時候越界
根據狀態表示方程進行填表
狀態方程是dp[i] = dp[i-1] + dp[i-2] + ap[i-3];
因此當i小于3的時候，越界
因此，初始化狀態表，dp[0] = 0;dp[1] = ap[2] = 1;

4、填表順序

從左往右填表，因為第n個位置的值，需要前面三個值已經計算好。

5、返回值

結果是第n個位置的值
所以，返回值就是dp[n]（因此需要多創建一個位置的空間）
?

2、代碼

class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1|| n == 2) return 1;//1、創建dp表vector<int> dp(n + 1);//2、初始化dp[0] = 0;dp[1] = dp[2] = 1;//3、填表for(int i = 3; i<=n; i++ )dp[i] = dp[i-1] + dp[i-2] + dp[i-3];//4、確定返回值return dp[n];        }
};

3、空間優化版本

//空間優化版本
class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1|| n == 2) return 1;int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <=n;i++){d = a+b+c;a = b;b = c;c = d;}return d;}
};

?題三

面試題 08.01. 三步問題 - 力扣（LeetCode）

1、算法解析

1、確定狀態：

定義 dp[i] 數組中的值到底表示什么意思？
很簡單，根據題目，就是到達該臺階一共有多少種走法。
我們的目標是求解 dp[n]，即上到第 n 階臺階的方式數量。

2、狀態轉移方程：

考慮小孩每次可以走 1 階、2 階或 3 階：

因此，狀態轉移方程為：
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]

3、初始化：

dp[0] = 1：上到第 0 階只有一種方式，就是不走任何臺階。
dp[1] = 1：上到第 1 階只有一種方式，就是從地面直接走一階。
dp[2] = 2：上到第 2 階有兩種方式，可以走兩次一階或者一次兩階。
為什么初始化這三個位置？因為他們需要前面三個位置的值，如果不初始化，會越界。

4、填表順序：

從 dp[3] 開始一直填充到 dp[n]。

5、返回值：

返回 dp[n]，因此要多創建一個位置的空間，同時由于結果可能很大，要對 dp[n] 模 1000000007 取余。

2、代碼

class Solution {
public:int waysToStep(int n) {if(n == 1) return 1;if(n == 2) return 2;// 1、創建dp表vector<int> dp(n + 1);// 2、初始化dp[0] = 1;dp[1] = 1;dp[2] = 2;// 3、填表for(int i = 3; i<n+1; ++i)dp[i] = ((dp[i-1] + dp[i-2]) % 1000000007 + dp[i-3]) % 1000000007;// 4、確定返回值return dp[n];}
};

??題四

91. 解碼方法 - 力扣（LeetCode）?

1、算法解析

1、確定狀態：

定義 dp[i] 數組中的值到底表示什么意思：dp[i]的值，就是以i為結尾的編碼串的最多解碼方式

2、狀態轉移方程：

?

因此，狀態轉移方程為：
dp[i] = dp[i-1] + dp[i-2]?

3、初始化：

為什么初始化這幾個位置？因為他們需要前面三個位置的值，如果不初始化，會越界。

4、填表順序：

從 dp[3] 開始一直填充到 dp[n]。

5、返回值：

返回 dp[n]

2、代碼

class Solution {
public:int numDecodings(string s) {//1、創建dp表int n = s.size();vector<int> dp(n);//只有一位dp[0] = s[0] == '0' ? 0 : 1;if(n == 1 ) return dp[0];//2、初始化//根據判斷條件進行初始化if(s[0] != '0' && s[1] != '0') dp[1]++;int m = (s[0] - '0')*10 + (s[1] - '0');//組合編碼if(m>=10 && m <= 26)dp[1] ++;//3、填表for(int i = 2; i<n; ++i){//i位置單獨編碼if( s[i] != '0') dp[i] += dp[i-1];//i和i-1位置組合編碼int x = (s[i-1] - '0')*10 + (s[i] - '0');if(x >= 10 && x <= 26) dp[i] += dp[i-2];}//4、返回值return dp[n-1];}
};