二叉樹1：深入理解數據結構第一彈——二叉樹（1）——堆-CSDN博客

二叉樹2：深入理解數據結構第三彈——二叉樹（3）——二叉樹的基本結構與操作-CSDN博客

二叉樹3：深入理解數據結構第三彈——二叉樹（3）——二叉樹的基本結構與操作-CSDN博客

前言：

在之前我們用C語言實現數據結構時，已經對二叉樹進行了系統的學習，但還是有一些內容并沒有涉及到，比如今天要講的二叉搜索樹，因為二叉搜索樹在C++中有現成的模板庫——set和map，并且實現起來較為麻煩，所以我們放到這里來講，對前面二叉樹部分有所遺忘的同學可以在我的主頁搜一下之前的文章看一下

目錄

一、二叉搜索樹的概念

二、二叉搜索樹的基本操作

1. 插入節點

2. 查找節點

3. 刪除節點

三、二叉搜索樹的實現

四、二叉搜索樹的應用

五、總結

---

一、二叉搜索樹的概念

二叉搜索樹又稱二叉排序樹，它是一種具有特殊性質的二叉樹，它具有以下特點：

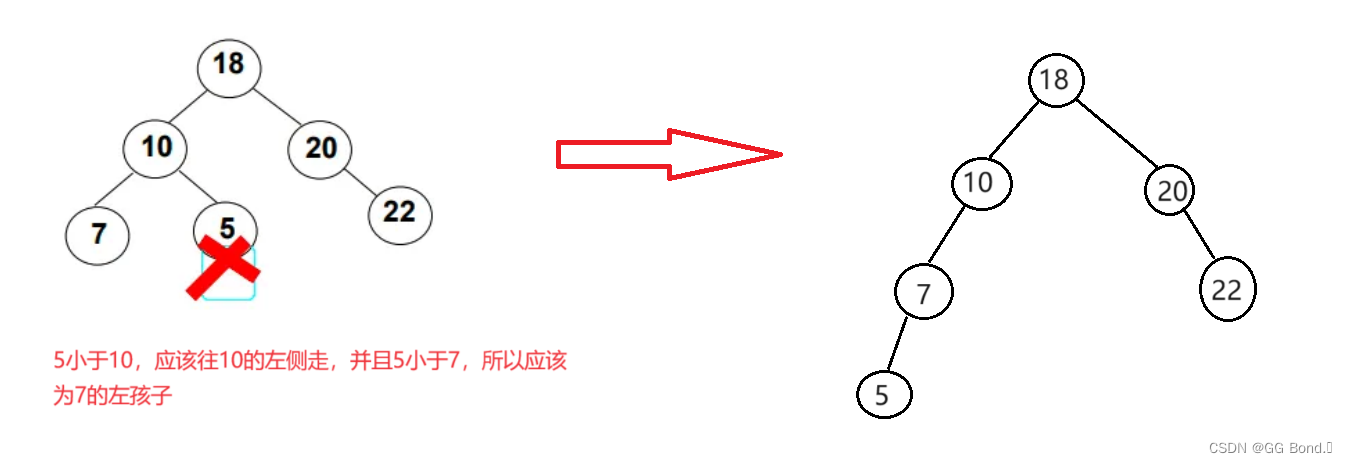
1. 有序性：對于樹中的每個節點，其左子樹中的所有節點的值都小于該節點的值，而其右子樹中的所有節點的值都大于該節點的值。

2. 唯一性：樹中的每個節點的值都是唯一的，不存在重復的值。

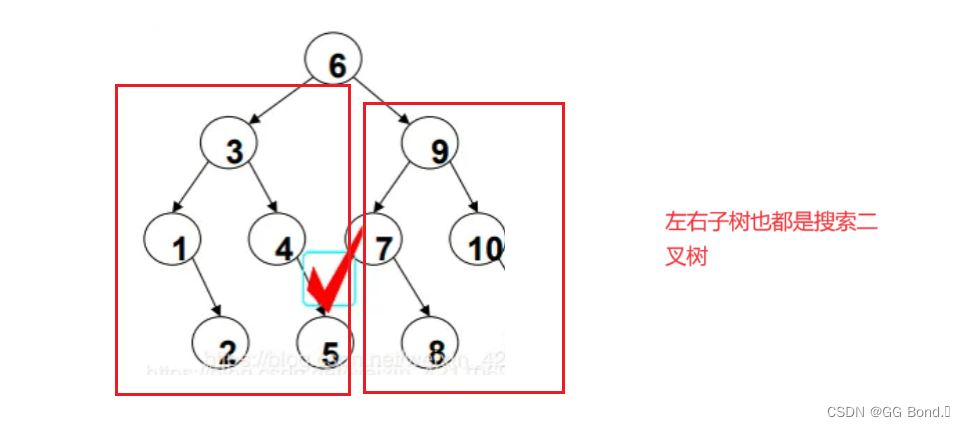
3. 遞歸性：它的子樹也都是二叉樹

上面這三種性質，最不好理解的應該是有序性，下面我們通過兩個例子來展現這三種性質：

二、二叉搜索樹的基本操作

1. 插入節點

插入節點的過程如下：

• 從根節點開始，比較要插入的值與當前節點的值。
• 如果要插入的值小于當前節點的值，則移動到左子節點；如果要插入的值大于當前節點的值，則移動到右子節點。
• 重復上述過程，直到找到一個空位置，然后在該位置插入新節點。

2. 查找節點

查找節點的過程如下：

• 從根節點開始，比較要查找的值與當前節點的值。
• 如果要查找的值等于當前節點的值，則返回該節點。
• 如果要查找的值小于當前節點的值，則移動到左子節點；如果要查找的值大于當前節點的值，則移動到右子節點。
• 重復上述過程，直到找到目標節點或遍歷到空節點。

3. 刪除節點

刪除節點的過程相對復雜，需要考慮以下幾種情況：

• 刪除葉子節點：直接刪除該節點。
• 刪除只有一個子節點的節點：將其子節點替換到該節點的位置。
• 刪除有兩個子節點的節點：找到該節點右子樹中的最小節點（或左子樹中的最大節點），將其值替換到該節點的位置，然后刪除該最小節點。

三、二叉搜索樹的實現

template<class T>
struct BSTNode
{BSTNode(const T& data = T()): _pLeft(nullptr) , _pRight(nullptr), _data(data){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;T _data;
};
template<class T>
class BSTree
{typedef BSTNode<T> Node;typedef Node* PNode;
public:BSTree(): _pRoot(nullptr){}// 自己實現，與二叉樹的銷毀類似~BSTree();// 根據二叉搜索樹的性質查找：找到值為data的節點在二叉搜索樹中的位置PNode Find(const T& data);bool Insert(const T& data){// 如果樹為空，直接插入if (nullptr == _pRoot){_pRoot = new Node(data);return true;}// 按照二叉搜索樹的性質查找data在樹中的插入位置PNode pCur = _pRoot;// 記錄pCur的雙親，因為新元素最終插入在pCur雙親左右孩子的位置PNode pParent = nullptr;while (pCur){pParent = pCur;if (data < pCur->_data)
比特就業課pCur = pCur->_pLeft;else if (data > pCur->_data)pCur = pCur->_pRight; ?// 元素已經在樹中存在elsereturn false;}// 插入元素pCur = new Node(data);if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;return true;}bool Erase(const T& data){// 如果樹為空，刪除失敗if (nullptr == _pRoot)return false;// 查找在data在樹中的位置PNode pCur = _pRoot;PNode pParent = nullptr;while (pCur){if (data == pCur->_data)break;else if (data < pCur->_data){pParent = pCur;pCur = pCur->_pLeft;}else{pParent = pCur;pCur = pCur->_pRight;}}// data不在二叉搜索樹中，無法刪除if (nullptr == pCur)return false;// 分以下情況進行刪除，同學們自己畫圖分析完成if (nullptr == pCur->_pRight){// 當前節點只有左孩子或者左孩子為空---可直接刪除}else if (nullptr == pCur->_pRight){// 當前節點只有右孩子---可直接刪除}else{
// 當前節點左右孩子都存在，直接刪除不好刪除，可以在其子樹中找一個替代結點，
比如：// 找其左子樹中的最大節點，即左子樹中最右側的節點，或者在其右子樹中最小的節
點，即右子樹中最小的節點// 替代節點找到后，將替代節點中的值交給待刪除節點，轉換成刪除替代節點}return true;}
// 自己實現void InOrder();
private:PNode _pRoot;
};

四、二叉搜索樹的應用

在我們目前的學習中，二叉搜索樹最重要的用途就是key--val模型，KV模型就是每一個key值都對應一個val值，這樣就形成一個<key,val>鍵值對，這樣的應用在生活中是非常常見的

比如：在菜市場中不同的蔬菜對應著不同的價格；新華詞典中，不同的漢字對應著不同的拼音，這些都可以用KV模型來解決

下面是KV模型的實現（沒有主函數）：

namespace kv
{template<class K,class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key,const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public://遍歷（中序）void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}///bool Insert(const K& key,const V& value){if (_root == nullptr){_root = new Node(key,value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key,value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 準備刪除  20:15繼續if (cur->_left == nullptr){//左為空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//右為空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//左右都不為空// 右樹的最小節點(最左節點)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;delete subLeft;}return true;}}return false;}BSTree() = default;~BSTree(){Destroy(_root);}//遞歸版本bool InsertR(const K& key){return _InsertR(_root, key);}bool FindR(const K& key){return _FindR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}BSTree(const BSTree<K,V>& t){_root = Copy(t._root);}BSTree<K,V>& operator=(BSTree<K,V> t){swap(_root, t._root);return *this;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{if (root->_left == nullptr){root = root->_right;return true;}else if (root->_right == nullptr){root = root->_left;return true;}else{Node* subLeft = root->_right;while (subLeft->_left){subLeft = subLeft->_left;}swap(root->_key, subLeft->_key);return _EraseR(root->_right, key);}}}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return root->_right;}else if (root->_key > key){return root->_left;}else{return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}Node* _root = nullptr;};
}

五、總結

以上就是二叉搜索樹的主要內容，在代碼實現上其實與之前講的二叉樹差別并不是很大，關鍵在于思路的梳理，這章就先到這了

感謝各位大佬觀看，創作不易，還請各位大佬點贊支持！！！