漢諾塔
漢諾塔(Tower of Hanoi),又稱河內塔,是一個源于印度古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定,在小圓盤上不能放大圓盤,在三根柱子之間一次只能移動一個圓盤。?
n = 1
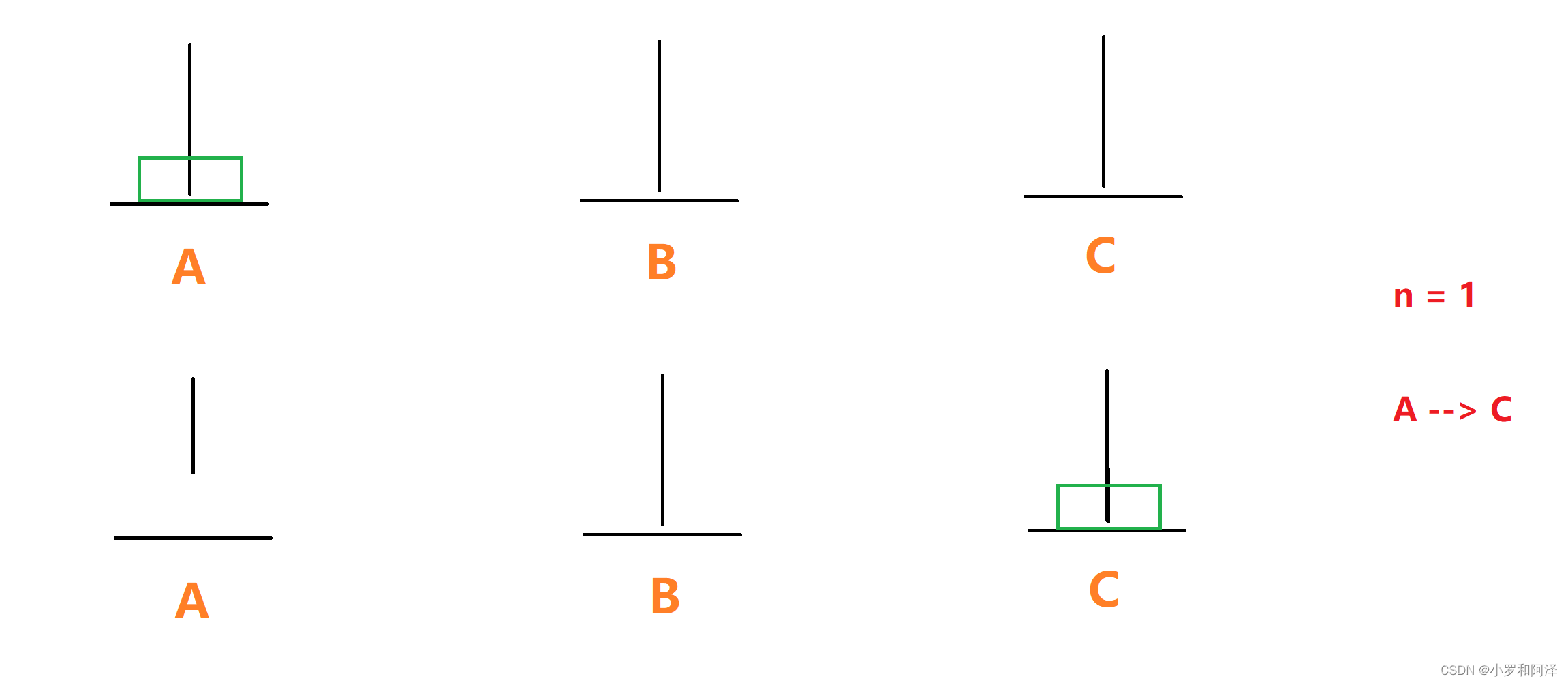
?n = 2
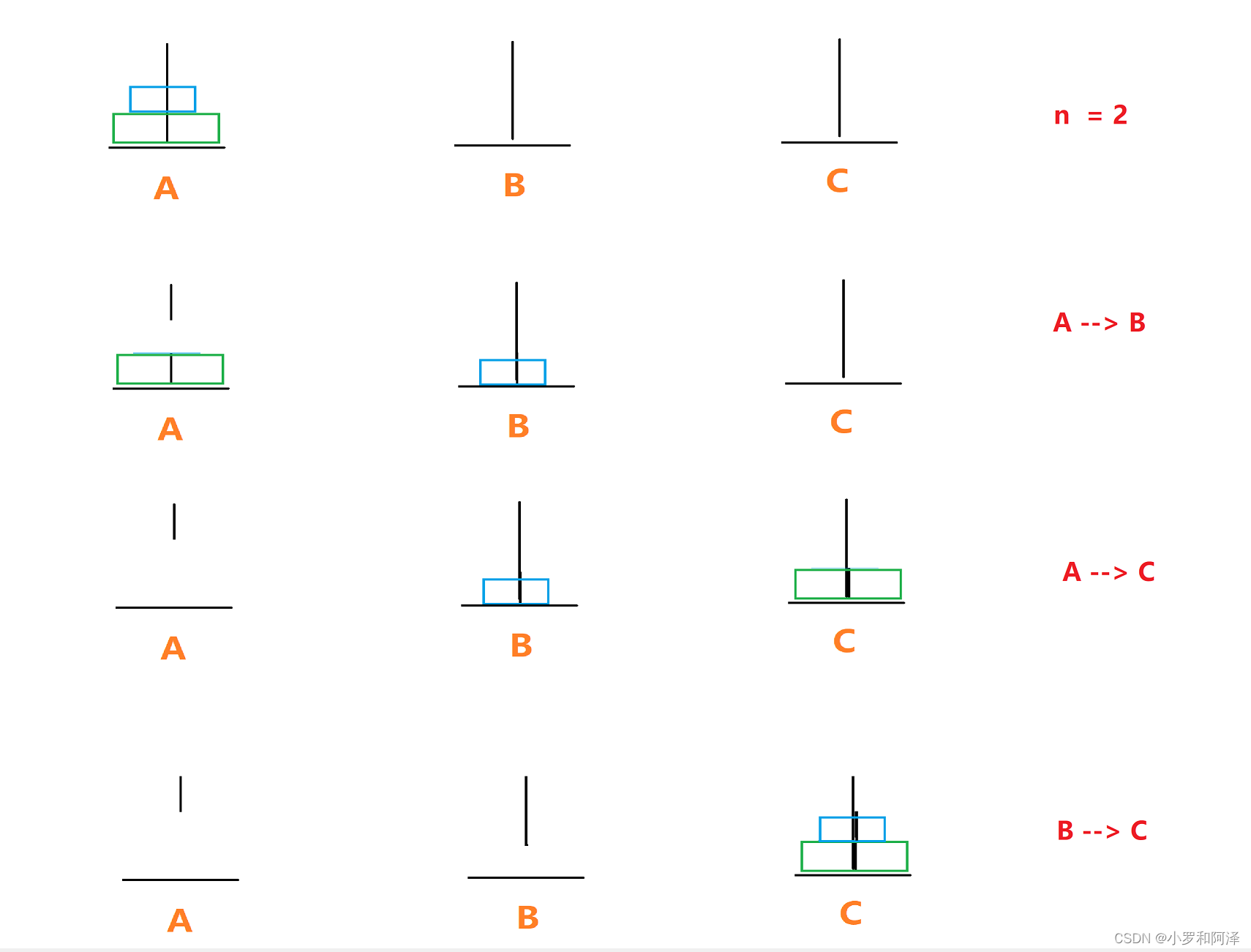
n = 3?
正常移動漢諾塔的步驟:
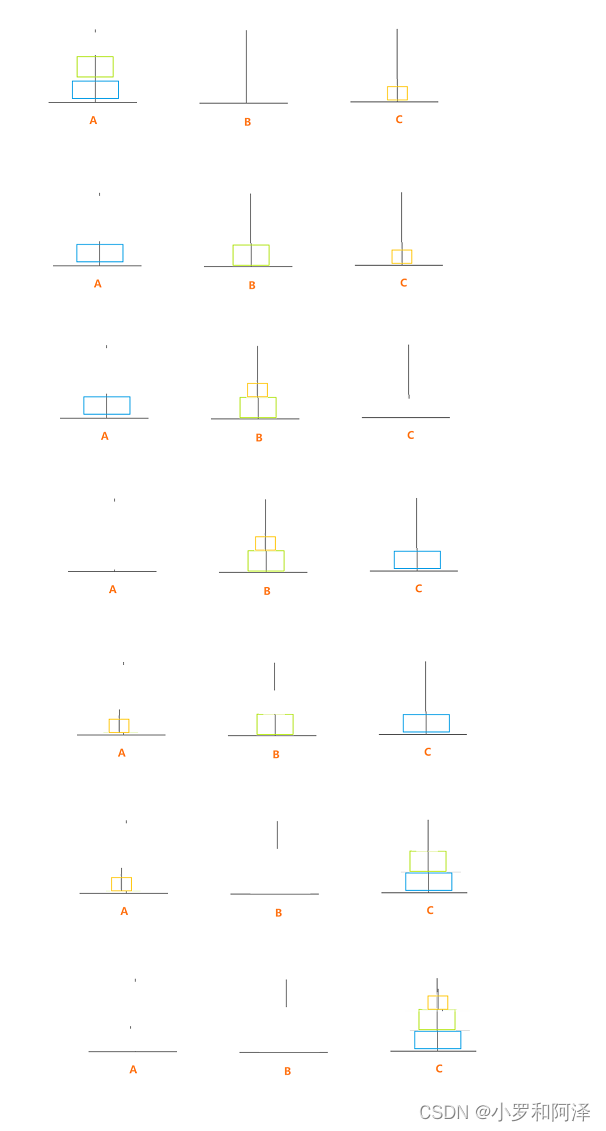
前面n = 1 和 n = 2 的時候 還比較簡單,我們可以直接挪動。
下面我們用遞歸的思想再移動一下:
遞歸 就是 將復雜的問題簡單化,詳細的說就是 一個復雜的大問題 可以 化解成 多個相同的小問題,而這些小問題 可以 利用遞歸的思想逐一的解決。?
提前聲明:
A : 起始位置
B : 中轉位置
C : 目標位置??
注意:此處的 起始位置 中轉位置 目標位置 并不是固定的,具體的需要看我們怎么傳參?

需要借助中轉位置 去 幫助我們實現 將最下面 一層圓盤 移動到 目標位置 上?
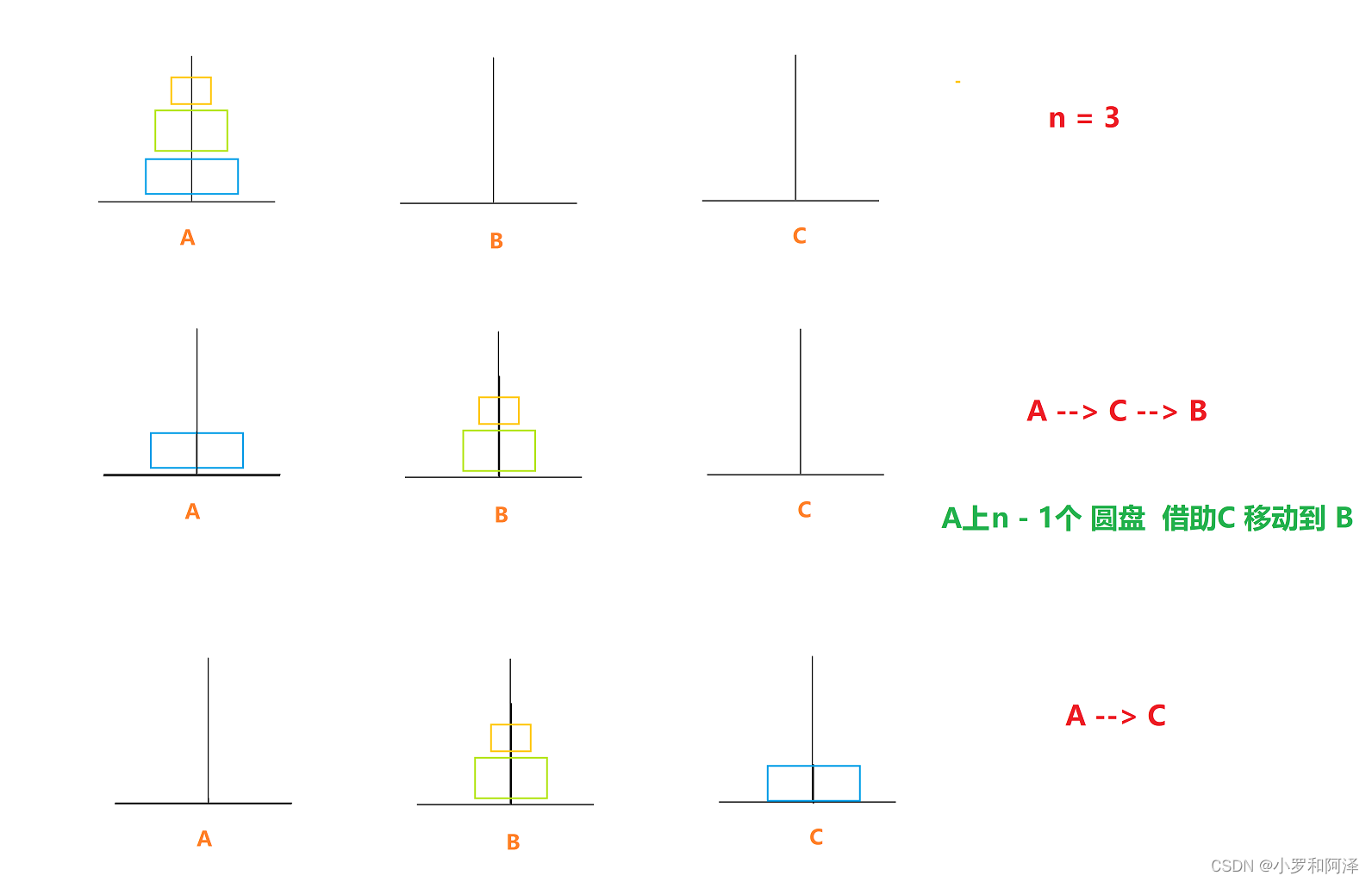
? ? ?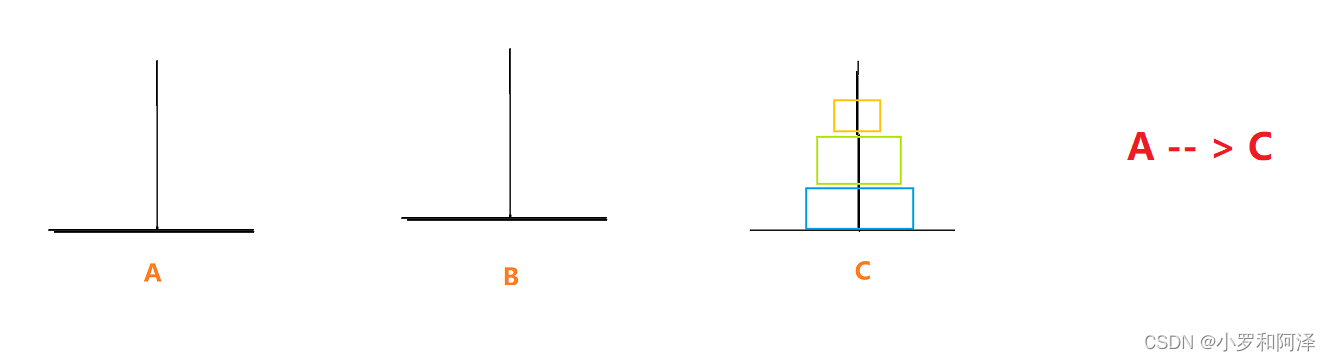
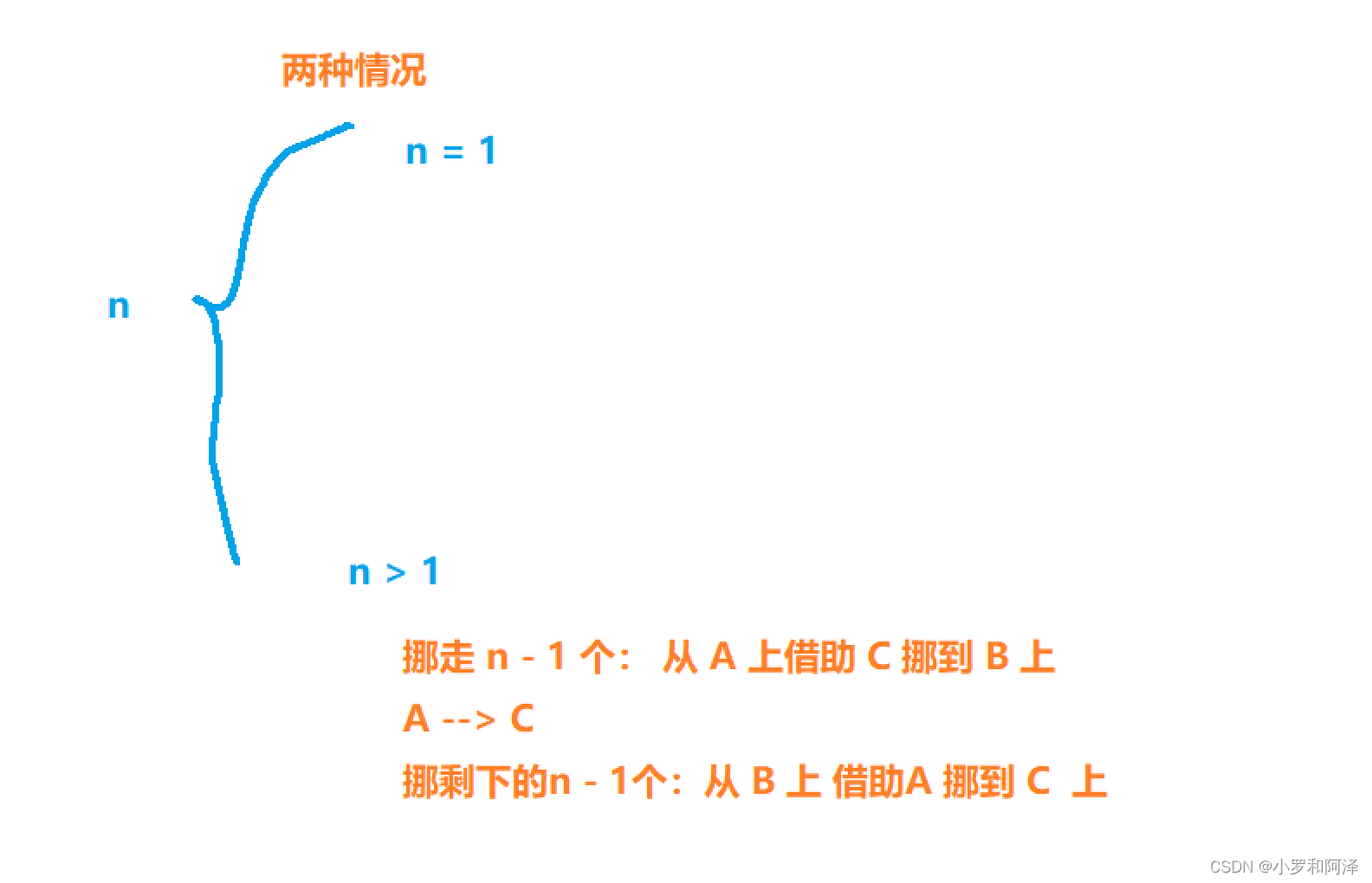
A 上 n - 1 個 圓盤 借助 C 移動到 B
解釋:?此處 將n - 1 個 圓盤 移動到??中轉位置 就需要遞歸的思想
我們 需要?把 n - 1 個圓盤 看作一個整體 直接 放到 B 上 (當然其中具體步驟還是比較麻煩的,但這些具體麻煩的步驟在遞歸中就已經實現了)
這時就體現我們遞歸的優點了,我們只需要關注 關鍵問題 其中比較繁瑣的步驟 我們可以直接忽略?(文章結尾的代碼 可以 清楚的看到)?
public static void move (char start, char end){System.out.print(start + " --> " + end + " ");
}/**** @param n 圓盤個數* @param pos1 起始位置* @param pos2 中轉位置* @param pos3 目標位置*/
public static void hanio (int n, char pos1 ,char pos2,char pos3){//結束遞過程的條件if(n == 1){move(pos1,pos3);}else {hanio(n-1,pos1,pos3,pos2); //將 n-1 個圓盤 看成一個整體 借助 pos3 位置 移動到 pos2move(pos1,pos3); //將最大最底層的 圓盤 放到 目標位置hanio(n-1,pos2,pos1,pos3); // 再將剩下的 n - 1 個 圓盤 從 pos2 借助 pos1 移動到 pos3}}public static void main(String[] args) {hanio(1,'A','B','C');System.out.println();hanio(2,'A','B','C');System.out.println();hanio(3,'A','B','C');System.out.println();hanio(4,'A','B','C');
}












- 需要自定義著色器)




)

