1.數值數據的表示

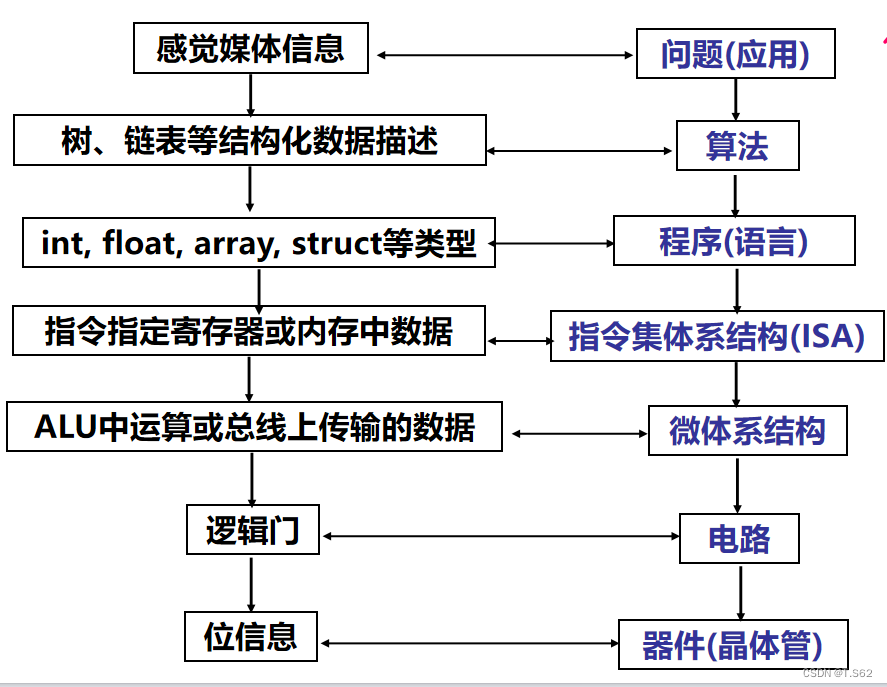
為什么采用二進制？

• 二進制只有兩種基本狀態，兩個物理器件就可以表示0和1
• 二進制的編碼、技術、運算規則都很簡單
• 0和1與邏輯命題的真假對應，方便通過邏輯門電路實現算術運算

數值數據表示的三要素

• 進位記數制（十進制、二進制、十六進制）
• 定浮點表示（解決小數點問題，定點小數：小數點固定居于最高位。定點數的原碼、補碼等還解決了正負號的問題）
• 如何用二進制編碼

原碼與補碼

首先我們先看原碼

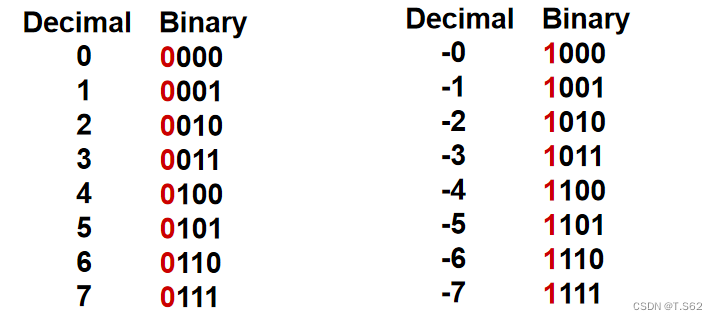
顯而易見，負數的表示就是最高位取1，但是這樣存在以下問題

• 0 的表示不唯一
• 加、減運算方式不統一
• 需額外對符號位進行處理
• 特別當 a<b時，實現 a-b比較困難

所以我們又引入補碼的概念（機器數就是補碼）

補碼=模+該數本身（mod模），該數最高位必須是0

我們就可以得到：123的補碼=0111 1011；-123的補碼=1000 0101，再多舉幾個例子，我們發現：

• 正數的補碼就是其本身
• 負數的補碼等于對應正數補碼的“各位取反、末位加1
• 正數補碼最高位是0，負數補碼最高位是1

以及一些結論：

對于某一確定的模，某數減去小于模的另一數，總可以用該數加上另一數負數的補碼來代替;

讓我們來舉一個例子：

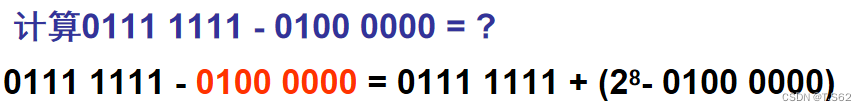
最后結果1 0011 1111，再將其mod2^8（運算器只有有限位，假設為n位，則運算結果只能保留低n位，因此，其模為2^n）,得到最終結果0011 1111

接下來是特殊數的補碼

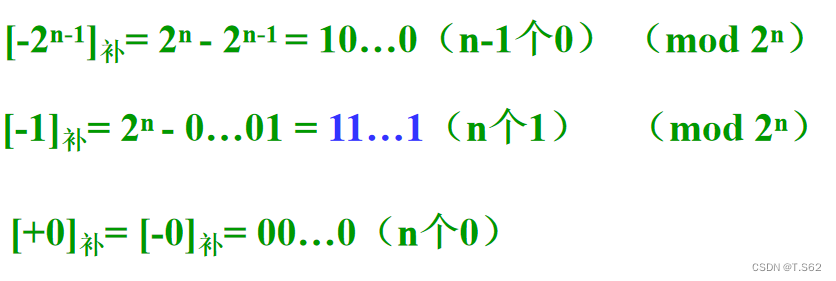
整數

整數分為無符號整數和有符號整數，例如8位無符號整數最大值1111 1111為255，有符號整數最大值0111 11111為127

c語言規定：若運算中同時有無符號和帶符號整數，則按無符號整數運算

浮點數

規格化數

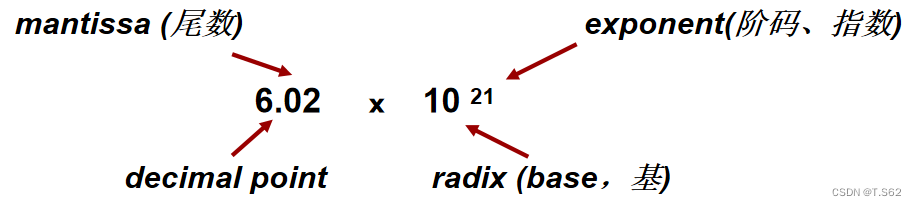
小數點前只有一位非零數

在計算機中，浮點數按如下格式存儲

s位是符號位，正數是0負數是1

注意：規格化尾數的小數點總是1，不寫進尾數M中

現在讓我們舉個例子，計算-12.75

首先12.75=1100.11；轉化為科學計數法1.10011*2^3；階數=3+127=130=1000 0010

尾數=100 1100 0000 0000 0000 0000；符號位為1

現在我們再來做一個題，反推

首先是負數；0111 1101是125，125-127=-2，指數為-2；根據尾數得1.11*2^-2；1.11又是1+0.5+0.25=1.75；所以最終的結果是1.75/4=0.4375

非規格化數

浮點數范圍比定點數大，但數的個數沒變多，故數之間更稀疏，且不均勻

說明浮點數不是能表示范圍內的任意數！

當輸入數據是一個不可表示數時，機器將其轉換為最鄰近的可表示數

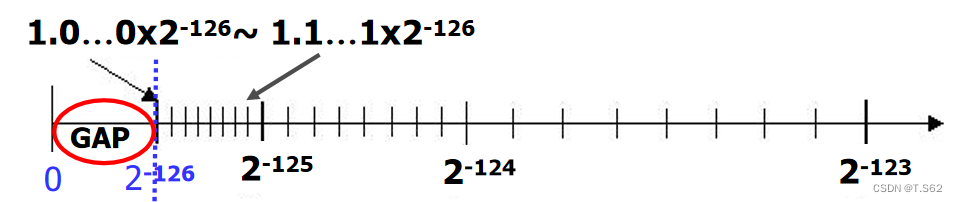
在浮點數中所能表示的最小正數1*2^-126,尾數不能全為0

為什么是-126？這樣可以使得出現比規格化數還小的數時程序也能繼續下去

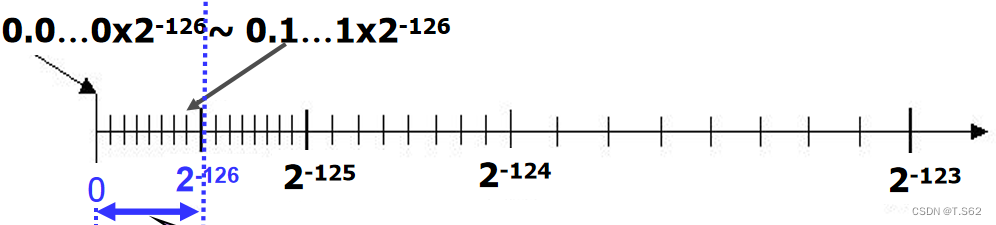
此時階數-126，而尾數的隱藏數變為0

無窮數

在浮點數中階數全為1并且尾數全為0則為無窮，如果尾數非零則是NaN

接下來，我們再來看計算機對于除數是0是怎么處理的：

計算機中除數為0的結果是 +/- ∞, 不是溢出異常.

這樣可以將X/0>Y可作為有效比較

然而Sqrt (- 4.0) 以及0/0為NaN

零

階數、尾數全為0，-0，+0表示不同

2.數據的存儲

數據的基本寬度

存儲器按字節編址，字節是最小可尋址單位 ，一般采用MSB（最高有效字節）

字與字長

字長：指數據通路的寬度

字：度量數據類型的寬度，16位（x86）

容量換算單位是1024，速度則是1000

大端：高地址存低字節

小端：高地址存高字節

譬如0x12345在小端機存儲的方式

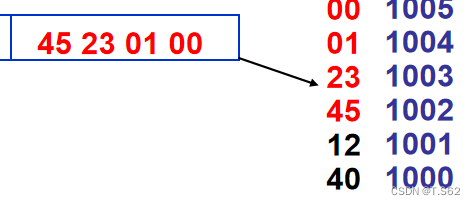
3.數據的運算

按位運算，邏輯運算與移位運算

按位運算

按位與：& 有零則零，兩個都是1才是1，1與任何數字與都是那個數本身

按位或：|，有1就是1，兩個都是0才是0

按位取反：~，1變0，0變1

按位異或：^,相同則為1，不同則為0

邏輯運算

&&，||，！，不做過多解釋

移位運算

左移：<<,擴大兩倍（可能會發生溢出）

右移：>>,縮小二分之一（可能有效數據丟失）

C語言中不區分是邏輯還是算術移位，編譯器根據x的類型確定

擴展：短轉長 ? ? ? ?無符號數：0擴展，前面補0；帶符號整數：符號擴展，前面補符

截斷：長轉短 ? ? ? 強行將高位丟棄，故可能發生“溢出”（沒有規定編譯器必須報錯）

算術運算

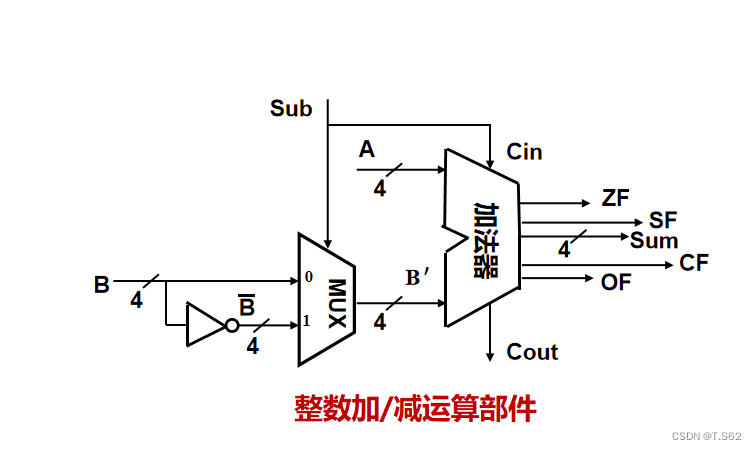
• ALUop:用來決定ALU所執行的處理功能。ALUop的位數k決定了操作的種類
• OF:溢出標志，若A.B同號，但與Sum不同號，則1
• SF:符號標志
• ZF：零標志，sum為0，則為1
• CF：進位/錯位標志。當加法時，CF=1,表示加法有進位；減法時，CF=1,表示減法不夠減
• Sub：為1時做減法，為0時做加法
• MUX：二路選擇器

ZF,SF,CF,OF被稱為條件標志，在運算電路中產生，被記錄到專門的的寄存器中

重要認識

• 計算機中所有算術運算都基于加法器實現！
• 加法器不知道所運算的是帶符號數還是無符號數。
• 加法器不判定對錯，總是取低n位作為結果，并生成標志信息

整數加法

無符號加溢出條件：CF=1

帶符號加溢出條件：OF=1

整數減法

Unsigned: CF=0時，大于

Signed：OF=SF時，大于

整數乘法

高級語言中兩個n位整數相乘得到的結果通常也是一個n位整數

無符號：若Puh=0，則不溢出

帶符號：若Psh每位都等于Ps的最高位，則不溢出

編譯器在處理變量與常數相乘時，往往以移位、加法和減法的組合運算來代替乘法運算

例如：對于表達式x*20，編譯器可以利用20=16+4=24+22，將x*20轉換為(x<<4)+(x<<2)

①無乘法指令>② 用ALU實現乘法指令>③用乘法器實現乘法指令

整數除法

對于帶符號整數來說，n位整數除以n位整數，除-2^(n-1)/-1= 2^(n-1)會發生溢出外，其余情況（除數為0外）都不會發生溢出

正數商取比自身小的最接近整數，負數商取比自身大的最接近整數

編譯器在處理一個變量與一個2的冪次形式的整數相除時，常采用右移運算來實現

注意：帶符號負整數（天板）：加偏移量(2^k-1)，然后再右移k 位 ，低位截斷

浮點數加減

首先要對階，小階向大階對齊，還要考慮舍入

若運算結果尾數是0，則需要將階碼也置0

附加位

IEEE754規定: 中間結果須在右邊加2個附加位

Guard (保護位)：在significand右邊的位 ?

Round (舍入位)：在保護位右邊的位；若沒有舍入位，采用就近舍入到偶數

舍入方式：

01：舍；11：入 ；10：(強迫結果為偶數)

因此

• int->float,不會發生溢出，但可能有數據被舍入
• int,float->double,能保留精確值
• double->float,int,可能發生溢出，此外，由于有效位數變少，故可能被舍入
• float,double->int,因為int沒有小數部分，所以數據可能會向0方向被截斷