快教程

10分鐘入門神經網絡 PyTorch 手寫數字識別

慢教程

【深度學習Pytorch入門】

簡單回歸問題-1

梯度下降算法

梯度下降算法

$$loss=x^2?sin(x)$$

求導得：

$$f^{‘}(x)=2xsinx+x^{2}cosx$$

迭代式：
$$x^{‘}=x?\delta x$$

$\delta x$ 前乘上學習速度 $lr$ , 使得梯度慢慢往下降無限趨近合適解，在最優解附近波動 ,得到一個近似解

求解器

• sgd
• rmsprop
• adam

求解一個簡單的二元一次方程

噪聲

實際數據是含有高斯噪聲的，我們拿來做觀測值，通過觀察數據分布為線型分布時，不斷優化loss，即求loss極小值

• $y=w?x+b+?$

• $?\backsim N(0.01,1)$

求解loss極小值，求得 $y$ 近似于$WX+b$ 的取值：
$$loss=(WX+b?y{)}^2$$
最后
$$loss=\sum _i(w?x_i+b?y_i{)}^2$$
從而
$$w^{‘}?x+b^{‘}\to y^{‘}$$

簡單回歸問題-2

凸優化(感興趣可以查閱資料)

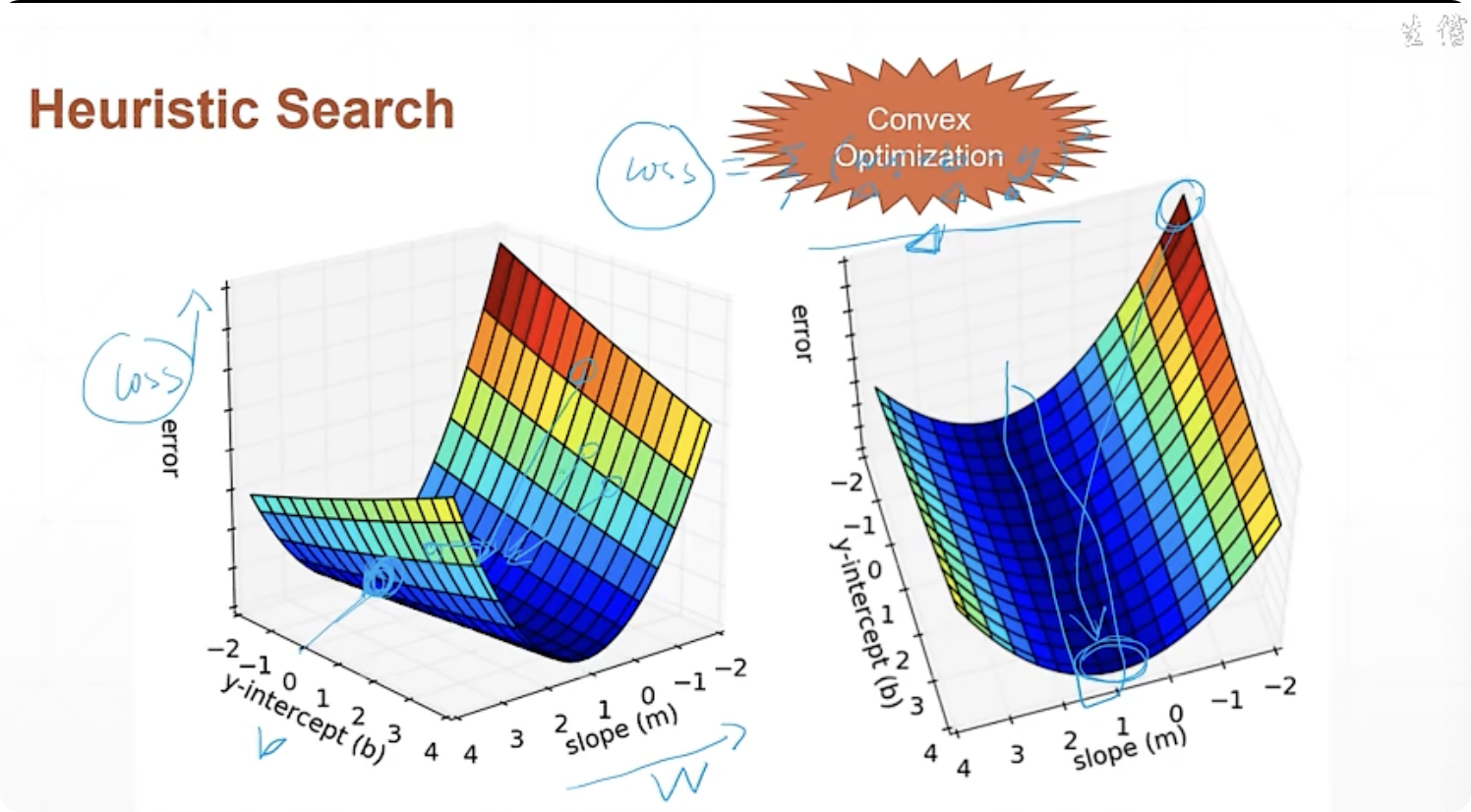
• linear Regression

取值范圍是連續的

$$\begin{gathered} wx+b \\ {w}_1+b \\ ....... \\ {w}_n+b \end{gathered}$$

用以上實際數據(8)預測 $WX+B$

# 梯度下降的應用
def compute_error_for_line_given_points(b,w,points):totalError = 0for i in range(0,len(points)):x = points[i,0]y = points[i,1]#  totalError += (y - (w * x + b ) ) ** 2b_gradient += -(2/N) * (y - ((w_current * x) + b_current))w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_w = w_current - (learningRate * w_gradient)return [new_b, new_w]#return totalError / float(len(points))def gradient_descent_runner(points, starting_b , starting_m, learning_rate, num_iterations):b = starting_bm = starting_mfor i in range(num_iterations):b, m = step_gradient(b,m,np.array(points),learning_rate)return [b,m]

• Logistic Regression

值域壓縮到 [0-1] 的范圍

• Classification

在上一種regression基礎上，每個點的概率加起來為1

簡單回歸實戰案例

import numpy as np# y = wx + b
def compute_error_for_line_given_points(b, w, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]totalError += (y - (w * x + b)) ** 2return totalError / float(len(points))def step_gradient(b_current, w_current, points, learningRate):b_gradient = 0w_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]b_gradient += -(2/N) * (y - ((w_current * x) + b_current))w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_m = w_current - (learningRate * w_gradient)return [new_b, new_m]def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):b = starting_bm = starting_mfor i in range(num_iterations):b, m = step_gradient(b, m, np.array(points), learning_rate)return [b, m]def run():points = np.genfromtxt("data.csv", delimiter=",")learning_rate = 0.0001initial_b = 0 # initial y-intercept guessinitial_m = 0 # initial slope guessnum_iterations = 1000print("Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m,compute_error_for_line_given_points(initial_b, initial_m, points)))print("Running...")[b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)print("After {0} iterations b = {1}, m = {2}, error = {3}".format(num_iterations, b, m,compute_error_for_line_given_points(b, m, points)))if __name__ == '__main__':run()

# 跑完結果
Starting gradient descent at b = 0, m = 0, error = 5565.107834483211
Running...
After 1000 iterations b = 0.08893651993741346, m = 1.4777440851894448, error = 112.61481011613473

分類問題引入-1

MNIST數據集

• 每個數字有7000張圖像
• 訓練數據和測試數據劃分為：60k 和 10k

H3:[1,d3]Y:[0/1/.../9]

(1) Nutshell

在最簡單的二元一次線性方程基礎上進行三次線性模型嵌套，使線性輸出更穩定，每一次嵌套后的結果作為后一個的輸入
p r e d = W 3 ? { W 2 [ W 1 X + b 1 ] + b 2 } + b 3 pred = W_3 *\{W_2[W_1X+b_1]+b_2\}+b_3\nonumber pred=W3??{W2?[W1?X+b1?]+b2?}+b3?

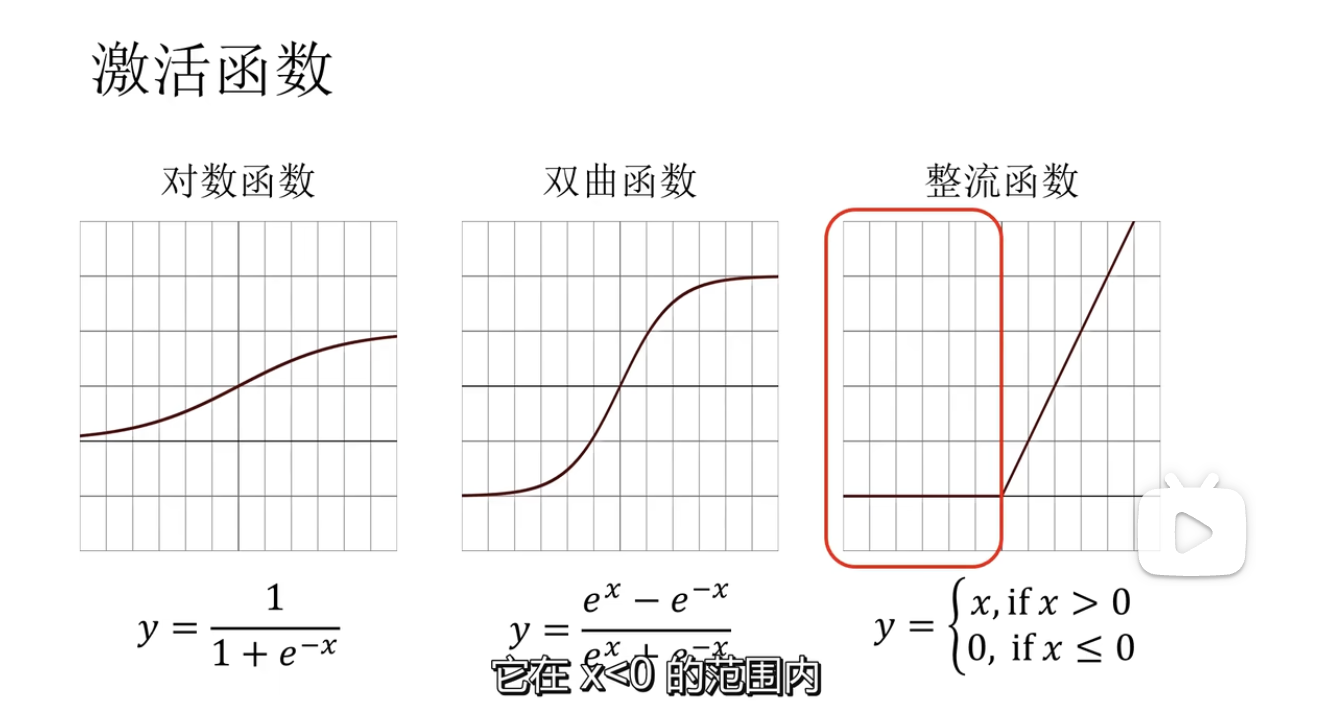
(2) Non-linear Factor

• segmoid

• ReLU

  • 梯度離散

    三層嵌套整流函數

    $H1=relu(XW1+b1)$

    $H2=relu(H1W2+b2)$

    $H3=relu(H2W3+b3)$

    增加了非線性變化的容錯

(3) Gradient Descent

$objective=\sum (red?Y{)}^2$

• $[W1,W2,W3]$
• $[b1,b2,b3]$

說人話就是讓模型愈來愈貼近真實的變化（從正常的字體，到傾斜，模糊，筆畫奇特等字體），以便更好的預測