柱狀圖中最大的矩形

題目

分析

矩形的面積等于寬乘以高，因此只要能確定每個矩形的寬和高，就能計算它的面積。如果直方圖中一個矩形從下標為 i 的柱子開始，到下標為 j 的柱子結束，那么這兩根柱子之間的矩形（含兩端的柱子）的寬是 j-i+1，矩形的高就是兩根柱子之間的所有柱子最矮的高度。

暴力解法（不可取）

? ? ? ? 如果能逐一找出直方圖中所有矩形并比較它們的面積，就能夠得到最大矩形的面積。方法為：采用嵌套的二重循環遍歷所有矩形，并比較他們的面積。該種方法的時間復雜度為O(N^2)，根據題目所給的提示可知，這種方法不能解決本題，會超時。

代碼為

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};

分治法（本題不可取）

? ? ? ? 仔細觀察直方圖可以發現，這個直方圖的最大矩形有3中可能：

第一種：矩形通過直方圖中最矮的柱子；

第二種：矩形的起始柱子和終止柱子都在直方圖中最矮柱子的左側；

第三種：矩形的起始柱子和終止柱子都在直方圖中最矮柱子的右側。

第二種和第三種從本質上來說和求整個直方圖的最大矩形面積是同一個問題，可以用遞歸函數解決。

代碼為：

class Solution {
public:int largestRectangleArea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};

單調棧法（可取）

? ? ? ? 下面介紹一種非常高效，巧妙的解法。這種解法用一個棧保存直方圖的柱子，并且在棧中的柱子的高度是遞增排序的。為了方便計算矩陣的高度，棧中保存的是柱子在數組中的下標，可以根據下標得到柱子的高度。

? ? ? ? 這種解法的基本思想是確保保存在棧中的直方圖的柱子的敢賭是遞增排序的。假設從左到右逐一掃描數組中的每根柱子，如果當前柱子的高度大于位于棧頂柱子的高度，那么將該柱子的下標入棧；否則，將位于棧頂的柱子的下標出棧，并且計算以位于棧頂的柱子為頂的最大矩形的面積。【注意：此時出棧須滿足：棧不為空并且棧頂柱子的高度大于等于當前柱子的高度】

????????以某根柱子為頂的最大矩形，一定是從該柱子向兩側眼神知道遇到比它矮的柱子，這個最大矩形的高是該柱子的高，最大矩形的寬是兩側比它矮的柱子中間的間隔。

? ? ? ? 如果當前掃描到的柱子的高小于位于棧頂柱子的高，那么將位于棧頂的柱子的下標出棧，并且計算以位于棧頂的柱子為頂的最大矩形的面積。由于保存在棧中的柱子的高度是遞增排序的，因此棧中位于棧頂前面的一根柱子一定比位于棧頂的柱子矮，于是很容易就能找到位于棧頂的柱子兩側比它矮的柱子。

? ? ? ? 當計算以當前柱子為頂的最大矩形的面積時，如果棧中沒有柱子，那么意味著它左側的柱子都比它高，因此可以想象在下標為 -1 的位置有一根比它矮的柱子。

? ? ? ? 當掃描數組中所以柱子之后，棧中可能仍然剩余一些柱子。因此，需要注意將這些柱子的下標出棧并計算以它們為頂的最大矩形的面積。

? ? ? ? 在掃描完數組中所有的柱子之后，當計算以當前柱子為頂的最大矩形的面積時，說明它的右側沒有比它矮的柱子，如果一根柱子的右側有比它矮的柱子，那么當掃描到右側較矮柱子的時候他就已經出棧了。因此，可以想象下標為數組長度的位置有一根比它矮的柱子。

? ? ? ? 由于已經計算了以每根柱子為頂的最大矩形面積，因此比較這些矩形的面積就能得到脂肪圖中的最大矩形面積。

代碼為

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();stack<int> st;st.push(-1);int maxarea=0;for(int i=0;i<n;i++){while(st.top()!=-1 && heights[st.top()]>=heights[i]){int height=heights[st.top()];st.pop();int width=i-st.top()-1;maxarea=max(maxarea,height*width);}st.push(i);}while(st.top() != -1){int height=heights[st.top()];st.pop();int width=n-st.top()-1;maxarea=max(maxarea,height*width);}return maxarea;}
};

最大矩形

題目

分析

? ? ? ? 上一道題是關于最大矩形的，這道題也是關于最大矩形的，他們之間有沒有某種聯系？如果能從矩陣中找出直方圖，那么就能通過計算直方圖中的最大矩形面積來計算矩陣中的最大矩形面積。

? ? ? ? 直方圖是由排列在同一基線上的相鄰柱子組成的圖形，由于題目要求矩形中只包含數字1，因此將矩陣中上下相鄰的值為1的各自看成直方圖中的柱子，如果分別以矩陣的每行為基線，就可以得到若干行由數字1的格子組成的直方圖。如下圖所示：

對應的直方圖如下：

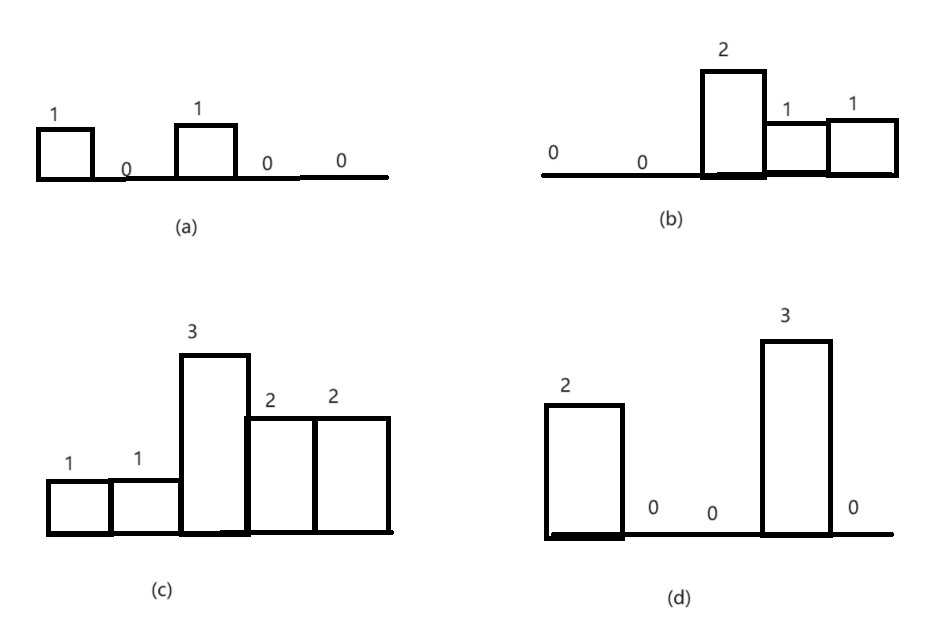
說明：（a）以矩陣第一行為基線的直方圖；（b）以矩陣第二行為基線的直方圖；（c）以矩陣第三行為基線的直方圖；（d）以矩陣第四行為基線的資方圖。

暴力解法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};

分治法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};

單調棧法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int> v){stack<int> st;st.push(-1);int area=0;for(int i=0;i<v.size();i++){while(st.top()!=-1 && v[i]<=v[st.top()]){int height=v[st.top()];st.pop();int width=i-st.top()-1;area=max(area,height*width);}st.push(i);}while(st.top()!=-1){int height=v[st.top()];st.pop();int width=v.size()-st.top()-1;area=max(area,height*width);}return area;}
};