自然語言處理（NLP）—

1. 主題建模的概念

????????主題建模（Topic Modeling）是一種用于發現文檔集合（語料庫）中的主題（或稱為主題、議題、概念）的統計模型。在自然語言處理和文本挖掘領域，主題建模是理解和提取大量文本數據隱藏主題的一種常用方法。

1.1 主題建模的關鍵特點

????????主題：在主題建模中，主題通常被定義為一組共現的詞匯，這些詞匯在語料庫中的文檔集合里代表了某種特定的概念或話題。
????????詞匯的概率：每個主題都由一組單詞及其相關概率構成，這些概率表示了單詞在該主題中的重要性或出現頻率。
????????單詞的多主題屬性：同一個單詞可以出現在多個主題中，并且在不同主題中具有不同的概率。這反映了詞匯在不同語境下的多義性。
????????主題的解釋性：生成的主題可能在語義上是有意義的，即它們代表了容易理解和識別的概念；也可能是抽象的，不容易直接解釋。

1.2 主題建模的算法

????????隱含狄利克雷分布（Latent Dirichlet Allocation, LDA）：LDA是最廣泛使用的主題建模算法之一。它假設文檔是由多個主題的混合生成的，每個主題又是由多個單詞的混合生成的。
????????非負矩陣分解（Non-negative Matrix Factorization, NMF）：NMF通過分解詞頻矩陣來發現文檔-主題和主題-詞匯之間的關系。

1.3 主題建模的應用

????????主題建模可以應用于許多場景，包括但不限于：

????????文檔分類：通過識別文檔的主要主題來對其進行分類。
????????推薦系統：通過發現用戶興趣的主題來提升內容推薦的相關性。
????????信息檢索：增強搜索算法，讓其能根據主題而非單個關鍵詞來檢索文檔。
????????趨勢分析：在時間序列數據中識別和跟蹤主題的流行度變化。

????????通過主題建模，研究人員和數據分析師能夠從大量的文本數據中抽象出有用的信息，以便進一步的分析和決策制定。

2.?潛在語義分析（Latent Semantic Analysis，LSA）

????????潛在語義分析（Latent Semantic Analysis，LSA）是一種用于文本處理的技術，可以揭示文檔集合中隱藏的語義結構。LSA通過數學模型捕獲詞語與文檔之間的關系，并能夠減少數據的噪聲和維度，從而發現詞義上的模式和趨勢。

2.1 LSA的關鍵步驟

2.1.1 構建術語/文檔矩陣M

????????每一行代表一個文檔，每一列代表一個術語（單詞）。

2.1.2?使用TF-IDF代替術語計數

$\text{tfidf}(w_0, d_0) = \text{occur}_{d_0}(w_0) \times \log \frac{\#d}{\#\{d | w_0 \in d\}}$

這里，

???????? $\text{tfidf}(w_0, d_0)$ 是單詞 $w_0$ 在文檔 $d_0$ 中的詞頻-逆文檔頻率值。
???????? $\text{occur}_{d_0}(w_0)$ 是單詞 $w_0$ 在文檔 $d_0$ 中出現的次數。
???????? $\#d$ 是文檔總數， $\#\{d | w_0 \in d\}$ 是包含單詞 $w_0$ 的文檔數。

2.1.3 執行奇異值分解（SVD）

????????奇異值分解是將矩陣M分解為三個矩陣的乘積： $M = U \Sigma V^T$ 。

???????? $\Sigma$ 是一個包含非負遞減實數的對角矩陣。
???????? $U$ 和 $V$ 是半正交矩陣（即滿足 $U^TU = I$ 或 $UU^T = I$ 的矩陣）。

????????LSA（潛在語義分析）是一種用于文本處理的技術，通過矩陣分解來識別文檔集合中的潛在主題。在LSA中，主要涉及三個矩陣：U、S和 $V^T$ 。

????????U矩陣：它具有與文檔數量相同的行數，其列由M的列聚合而來，這些列代表主題，因此U是一個文檔-主題矩陣。
???????? $V^T$ 矩陣：它的列數與M中的術語數量相同，其行由M的行聚合而來，這些行代表與U中相同的主題，因此V是一個術語-主題矩陣。
????????決定主題數量N：在LSA中，我們需要決定主題的數量N，這是一個重要的參數，因為它影響模型的性能和主題的解釋性。

2.1.4?獲得最優的主題數量N

????????要獲得最優的主題數量N，沒有一個統一的標準答案，但可以通過以下方法來估計：

????????試錯法：選擇不同的N值，分別構建模型，然后評估每個模型的性能和主題的解釋性。通常，可以使用諸如困惑度（Perplexity）之類的指標來評估模型的性能，低困惑度通常意味著模型性能好。

????????主題一致性：評估模型生成的主題的一致性或穩定性。主題一致性高的模型傾向于產生具有明確含義的、相互區分度高的主題。

????????人工評估：通過專業知識對生成的主題進行評估，選擇能夠最好地反映文檔集合內容的主題數量。

2.1.5?降維

????????取 $U$ 的前N列， $\Sigma$ 的前N行和列，以及 $V^T$ 的前N行來減少問題的維度。
????????這樣做是為了保留數據中最重要的語義特征，同時去除那些對于主題不太重要或者是噪聲的維度。

2.2?LSA的應用

????????發現文檔和術語之間的隱含關系：LSA可以幫助識別文檔中的主題或概念，并將術語與這些主題或概念關聯起來。

????????改進信息檢索：通過更好地理解文檔內容的語義，LSA可以提高搜索引擎的準確性。

????????文本聚類和分類：LSA的降維特性可以用于文本聚類和分類任務，提高模型性能。

????????LSA雖然是一個較為古老的方法，但它仍然是文本挖掘和自然語言處理中一個非常有價值的工具。通過揭示文本數據中的隱含語義結構，LSA能夠支持各種文本分析任務。

2.3 主題示例

????????主題示例展示了通過LSA技術從文檔集合中提取的不同主題。每個主題都是由一系列術語組成，這些術語代表了主題的核心內容。例如，主題0可能與面試有關，而主題1可能與警察、事故和法庭相關。通過分析這些主題，我們可以對文檔集合中的內容有更深入的了解，每個主題提供了文檔集中某個特定方面的視角。

Topic 0:
interview extended michael john david smith james andrew mark scott
Topic 1:
police death probe crash woman fire call court missing drug
Topic 2:
say plan council call govt back fire australia water court
Topic 3:
say australia police minister need report must world could labor
Topic 4:
court face fire woman murder charged charge accused death crash
Topic 5:
call say medium australia inquiry change prompt spark opposition health
Topic 6:
fire house home govt crew australia sydney school blaze threat
Topic 7:
australia back world south australian take first test lead win
Topic 8:
council australia fire rate rise seek woman considers coast land
Topic 9:
back council claim fight fire hit say take push market

????????選擇最優主題數量的過程涉及到綜合考量模型的解釋性、性能指標以及實際應用需求。在實際操作中，可能需要多次嘗試和評估，以找到最適合特定文檔集合的主題數量。此外，通過觀察和解釋每個主題中最重要的術語，研究者可以更好地理解文檔集合的潛在結構和含義。

????????每個主題下列出的術語反映了與該主題相關聯的關鍵概念和實體，通過這些術語，可以快速把握每個主題的核心內容。例如，主題1聚焦于與法律、緊急情況和安全相關的事件，而主題7則可能關注于體育競賽和國際競賽成績。

????????潛在語義分析不僅能幫助我們發現文本數據中的隱含主題，還可以用于文檔分類、信息檢索、文本相似性分析等多種應用場景，從而提高信息檢索的準確性和文本分析的深度。

3. LDA?

????????Latent Dirichlet Allocation (LDA) 是一種廣泛應用于文本挖掘和主題建模的統計模型，它能夠從大量的文檔集合中發現隱含的主題結構。LDA 基于 Dirichlet 分布作為其核心數學原理之一，以此來模擬文檔中主題的分布以及主題中詞匯的分布。

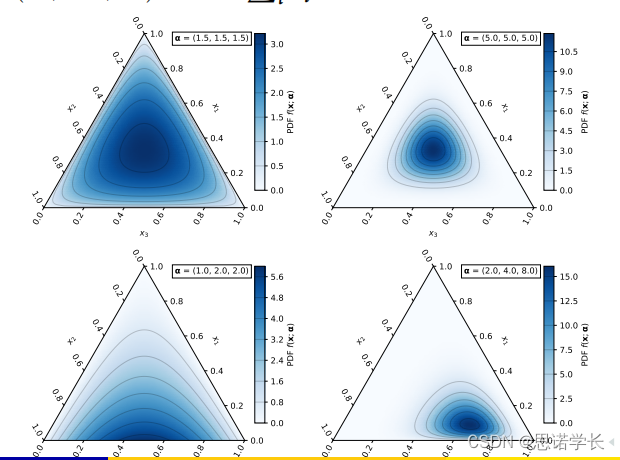
3.1 Dirichlet 分布簡介

????????Dirichlet 分布是一個連續多變量概率分布，它是對多項分布中參數的先驗分布。簡單來說，如果你有一個多項分布（即一個分布，其中的事件有多個可能的類別，比如擲骰子的六個面），Dirichlet 分布可以用來表示這些類別分布的不確定性。

????????Dirichlet 分布的參數是一組正實數 $\alpha = (\alpha_1, \ldots, \alpha_n)$ ，這些參數本身被稱為"濃度參數"。分布的結果是一組滿足以下條件的值 $(x_1, \ldots, x_n)$ ：

????????每個 $x_i$ 都在 0 和 1 之間，即 $0 \leq x_i \leq 1$ 。

????????所有 $x_i$ 的總和為 1，即 $\sum_{i=1}^{n}x_i = 1$ 。

????????這些性質使得 Dirichlet 分布非常適合表示一個文檔中不同主題的比例，或者一個主題中不同詞匯的比例，因為這兩種情況都涉及到了一系列比例的表示，且這些比例的總和為 1。

3.2?LDA 中的應用

????????在 LDA 模型中，Dirichlet 分布被用作兩個層次的先驗分布：

????????文檔-主題分布：每個文檔都被假設為由多個主題組成，其比例遵循 Dirichlet 分布。參數 $\alpha$ 反映了主題分布的先驗知識，比如我們假設文檔中各個主題的分布是均勻的，還是有某些特定主題更可能出現。

????????主題-詞匯分布：同樣地，每個主題被假設為由多個詞匯組成，其比例也遵循 Dirichlet 分布。參數 $\beta$ （通常與 $\alpha$ 不同）反映了詞匯分布的先驗知識。

????????通過這種方式，LDA 能夠自動從文檔集合中學習到隱含的主題，并且能夠表達出每個文檔中這些主題的比例以及每個主題中不同詞匯的比例，這對于文本分析和理解具有重要價值。

3.3?LDA潛在狄利克雷分配的圖形模型

????????

3.3.1 圖形參數的解釋? ? ? ??

????????這張圖是一個Latent Dirichlet Allocation（LDA，潛在狄利克雷分配）的圖形模型，用來展示如何從文檔中抽取主題和它們的分布。在這個模型中：

????????α（Alpha）：這是一個參數，影響文檔中主題分布的形狀。一個較大的α值可能意味著每個文檔包含的主題更均勻分布，而較小的α值意味著文檔更可能傾向于一小部分主題。α是大小為K的向量，其中K是主題的數量，我們對M個文檔進行這樣的處理。

????????θ（Theta）：表示一個特定文檔中不同主題的分布，它是從Dirichlet(α)分布中抽樣得到的。

????????Z：這是主題分配變量，表示給定文檔中的每個詞被分配到的主題。

???????? W：這是觀察到的單詞變量，代表文檔中的實際單詞。

????????β（Beta）：這是一個參數，影響主題中詞匯分布的形狀。和α參數類似，一個較大的β值表示每個主題中詞匯分布更均勻，而較小的β值表示某些詞匯在主題中的權重更重。β是大小為V的向量，V是詞匯表的大小，我們對K個主題進行這樣的處理。

?????????（Phi）：表示一個特定主題中不同詞匯的分布，它是從Dirichlet(β)分布中抽樣得到的。

????????在這個模型中，每個文檔都通過其θ向量有一個主題分布，θ向量是從α參數的Dirichlet分布中采樣得到的。同樣，每個主題都通過其?向量有一個詞匯分布，?向量是從β參數的Dirichlet分布中采樣得到的。這種結構允許每個文檔表現出多個主題，每個主題也包含多個詞匯。通過這種方式，LDA可以發現隱藏在大量文本數據背后的主題結構，這對于文本挖掘和信息檢索非常有用。

3.3.2 在LDA模型中的處理步驟

????????LDA（潛在狄利克雷分配）是一種主題模型，它允許我們對文檔集合中的文檔和詞匯進行主題分配。對于給定的文檔，在LDA模型中的處理步驟如下：

? ? ? ? a.為每個詞匯選擇主題：對于文檔中的每個詞匯（文檔中共有N個詞匯），我們從多項分布Polynomial(θ)中抽取一個樣本主題。這里的θ是這個文檔的主題分布，它表示不同主題在該文檔中的比例。

? ? ? ? b.確定詞匯屬于主題的概率：對于每個詞匯，我們也有一個概率φ（phi），它表示該詞匯屬于給定主題的概率。φ是由該主題的詞匯分布決定的，這個分布說明了每個詞匯屬于該主題的可能性。

? ? ? ? c.計算主題與文檔的關聯概率：我們可以計算文檔中每個詞匯屬于不同主題的概率。這是通過θ和φ的乘積得到的，因為θ給出了文檔屬于各個主題的概率，而φ給出了每個主題中各個詞匯的概率。

? ? ? ? d. 利用這些概率在算法中：通過結合文檔的主題概率θ和詞匯的主題概率φ，我們可以估計文檔中每個詞匯屬于各個主題的概率。這些概率可以用來推斷文檔的主題結構，以及主題本身的詞匯構成。

? ? ? ? e. 迭代優化：LDA通常使用迭代算法（如吉布斯抽樣或變分貝葉斯方法）來優化θ和φ，使得模型能夠最好地解釋觀測到的詞匯分布。這些迭代算法通過調整θ和φ的估計來最大化數據的似然性或某些后驗概率。

????????在多次迭代之后，我們得到了穩定的主題分布θ和詞匯分布φ，這樣就能對每個文檔的主題構成以及每個主題中詞匯的重要性有了較好的估計。這允許我們對文檔進行分類、理解其內容、以及探究不同主題之間的關系。

3.3.3 LDA算法

????????LDA（潛在狄利克雷分配）算法是一個用于發現文本集合中潛在主題的過程。以下是其步驟的中文解釋：

????????a. 隨機分配主題：在所有文檔中，我們隨機給每個詞匯分配一個主題。

????????b. 準備表格：建立兩個表格，一個記錄每個文檔中各個主題的出現次數，另一個記錄每個詞分配給主題的情況。

????????c. 循環所有詞匯：對所有文檔中的每個詞匯開始循環。假設我們現在處理的是文檔 $d_i$ 中的詞匯 $w_j$ ，這個詞匯當前分配到主題 $t_k$ 。現在，我們把這個詞匯從它當前的主題中去除，并在第1步建立的兩個表格中各減去一個單位。

????????d. 計算概率并更新分配：然后，我們計算這個詞匯屬于每個主題的概率，并重新為它分配一個最有可能的主題。具體計算如下：

???????? $P(t_k | d_i)$ 是文檔 $d_i$ 中分配給主題 $t_k$ 的詞匯比例，計算公式為 $\frac{n_{i,k} + \alpha}{N_i - 1 + K\alpha}$ ，其中 $n_{i,k}$ 是文檔 $d_i$ 中分配到主題 $t_k$ 的詞的數量， $N_i$ 是文檔 $d_i$ 的總詞數， $\alpha$ 是平滑超參數。
? ?
???????? $P(w_j | t_k)$ 是主題 $t_k$ 生成詞匯 $w_j$ 的概率，計算公式為 $\frac{m_{j,k} + \beta}{\sum_{j \in V} m_{j,k} + V\beta}$ ，其中 $m_{j,k}$ 是詞匯 $w_j$ 分配給主題 $t_k$ 的次數， $V$ 是詞匯表的大小， $beta$ 是另一個平滑超參數。

????????e. 主題重新分配：我們選擇使 $P(t_k | d_i)P(w_j | t_k)$ 最大的 $t_k$ 作為詞匯 $w_j$ 的新主題，并更新表格。

????????f. 重復步驟2到4：對所有文檔中的每個詞匯重復以上步驟。

????????g. 多次迭代：重復步驟1到5指定的迭代次數，直到算法穩定，通常這個過程會逐步提高整個模型的準確性。

????????通過這個迭代過程，LDA算法能夠發現文檔集合中的主題，并估算文檔中詞匯分布以及詞匯與主題之間的關聯。這個模型非常有用，可以幫助我們理解和組織大量的文本數據。

4. 總結LSA（潛在語義分析）與LDA（潛在狄利克雷分配）

????????LSA（潛在語義分析）與LDA（潛在狄利克雷分配）都是用于從文本數據中抽取主題的技術，但它們在數學原理和應用效果上有所不同。

????????LSA的主題是通過奇異值分解（SVD）從術語-文檔矩陣中提取的。這種方法基于線性代數，能夠減少數據的維度，挖掘詞和文檔之間的關系。

????????LDA的主題是通過迭代計算每個文檔的主題分布和每個主題的詞分布來得到的。這個過程基于統計推斷，特別是貝葉斯推斷，能夠更好地處理文本數據的多義性和噪聲。

????????以下是兩種方法各自提取的主題內容：

????????LSA的主題示例：

????????主題0：與個人采訪有關的關鍵詞。
????????主題1：涉及警察、死亡、事故調查等安全問題。
????????主題2：關于政府規劃、議會活動及政府決策。
????????主題3：包括有關澳大利亞、警察、政府官員的話題。
????????主題4：與法庭、火災、謀殺案和其他重大事件有關。
????????...（依此類推，總結每個主題的核心內容）

????????LDA（100次迭代后）的主題示例：

????????主題0：涉及事故報告、市場、失蹤案件等。
????????主題1：與政府政策、水資源管理、農業相關的話題。
????????主題2：包括警察、女性、學校、國家事務等內容。
????????主題3：圍繞醫院、健康、政府選舉、勝利等議題。
????????主題4：變化、農村事務、談話、價格上漲等話題。
???????? ...（依此類推，總結每個主題的核心內容）

????????在實際應用中，LDA通常被認為比LSA更先進，因為它考慮到了詞的多義性和文本數據中的不確定性。LDA的主題通常也更加一致和清晰。然而，這兩種技術都能提供有價值的見解，選擇哪種方法取決于具體的應用場景和需求。

5. 主題一致性的評估方法

????????評估主題的一致性是主題模型質量評估的關鍵環節。它用于衡量一個主題中的詞是否經常共同出現，這樣的主題通常對人類來說更加連貫、更易理解。Newman等人（2010年）和Mimno等人（2011年）提出的UCI一致性和UMass一致性就是這樣的評估指標。

5.1 UCI一致性

????????UCI一致性使用了PMI（逐點互信息）作為計算的基礎。

????????PMI是一種統計量，用于衡量兩個詞$w_i$和$w_j$共同出現的頻率是否高于隨機共同出現的頻率。

????????通過在維基百科等大型語料庫上使用滑動窗口來計算共現概率，PMI的計算公式為：

$PMI(w_i, w_j) = \log \left( \frac{P(w_i, w_j) + \epsilon}{P(w_i)P(w_j)} \right)$

????????其中， $P(w_i, w_j)$ 是兩個詞共現的概率， $P(w_i)$ 和 $P(w_j)$ 分別是兩個詞獨立出現的概率， $\epsilon$ 是一個小的正數，用于避免對數運算中的除零錯誤。

????????UCI一致性是通過對一個主題中所有可能的詞對 $(w_i, w_j)$ 計算PMI并求和得到的。

5.2 UMass一致性

????????UMass一致性與UCI類似，但它是一個不對稱的量度，只考慮特定順序的詞對。
????????UMass一致性的計算方法為：

$C_{UMass} = \frac{2}{N(N - 1)} \sum_{i=2}^{N} \sum_{j=1}^{i-1} \log \left( \frac{P(w_i, w_j) + \epsilon}{P(w_j)} \right)$

????????其中， $P(w_i, w_j)$ 是兩個詞共現的概率， $P(w_j)$ 是第一個詞出現的概率。

5.3 一致性結果CUCI

????????負的PMI值意味著詞的組合趨勢比隨機組合更低。
????????根據您提供的數據，LSA的一致性分數是?1.439，LDA經過1次迭代后是?2.140，10次迭代后是?1.957，100次迭代后是?1.921。
????????這些數值表示LDA模型隨著迭代次數的增加一致性有所提高，也就是說模型的質量在逐漸變好，詞更傾向于與其他相關詞共同出現。

????????在使用這些指標時，較高（較不負）的一致性分數通常表明模型的主題更加連貫，與人類的判斷更為一致。在實際應用中，選擇最佳的主題模型往往需要綜合這些指標與其他因素，如主題的解釋性和應用的特定需求。