455.分發餅干

先給孩子和餅干排序，每次選取一個最大的餅干給一個最大胃口的孩子，直到餅干分完或者遍歷完孩子

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1;int res = 0;for (int i = g.size() - 1; i >= 0; i--) {if (index >= 0 && s[index] >= g[i]) {index--;res++;}}return res;}
};

或者換一種想法，從小到大遍歷餅干，每次分配一個餅干給小朋友，能給index就++

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = 0;for (int i = 0; i < s.size(); i++) {if (index < g.size() && s[i] >= g[index]) {index++;}}return index;}
};

376.擺動序列

如果只有一個元素，則答案為1
如果有兩個元素，則如果兩個元素不相同，答案為2，否則為1
這是需要注意的地方

本題需要繪制一個圖，能看出來峰值的關系

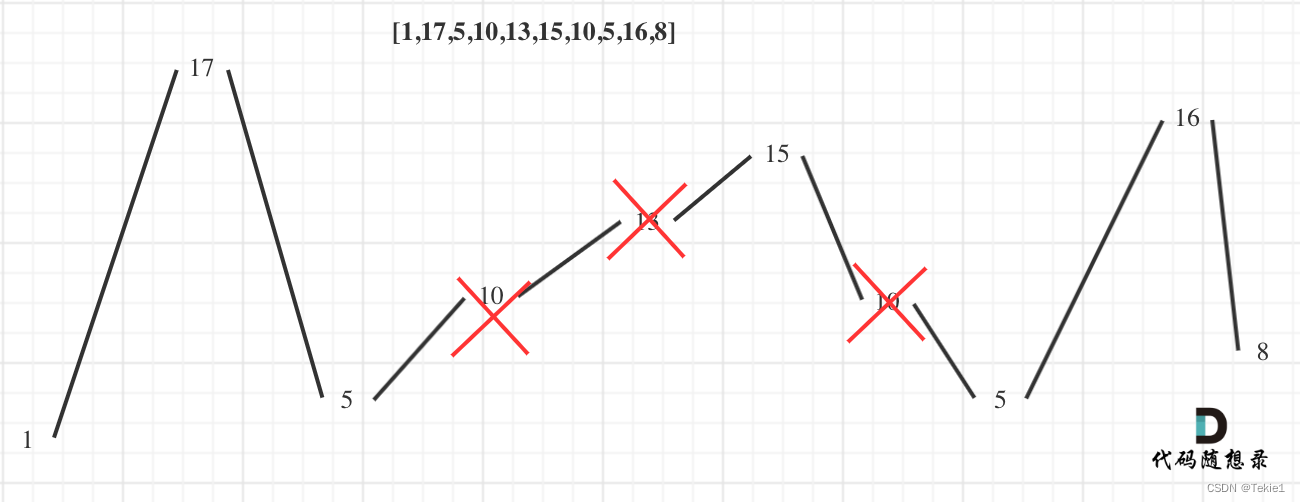
只需要把那些非峰值上的點刪除，就是最長的擺動序列
因為對于非峰值的點，其都是無關緊要的
當坡度發生變化時，只需要找到該坡度里的極點即可

局部最優：刪除單調坡度上的節點（不包括單調坡度兩端的節點），那么這個坡度就可以有兩個局部峰值。
整體最優：整個序列有最多的局部峰值，從而達到最長擺動序列

本題要考慮三種情況：

情況一：上下坡中有平坡

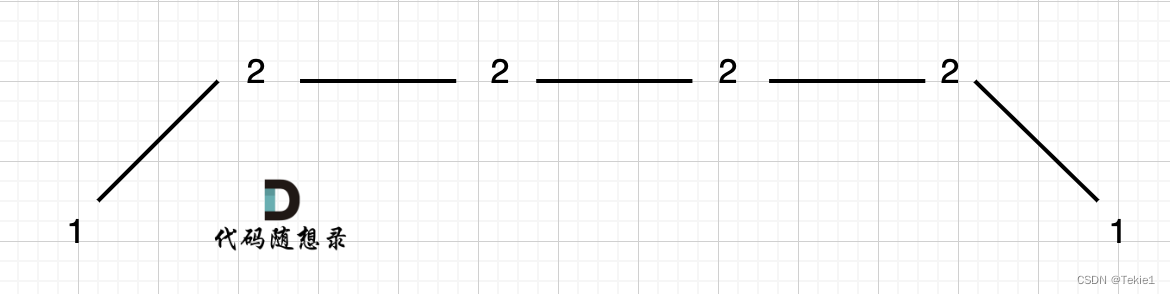
可以統一規則，刪除前面的3個2，留下最后一個，序列變成[1,2,1]，答案為3

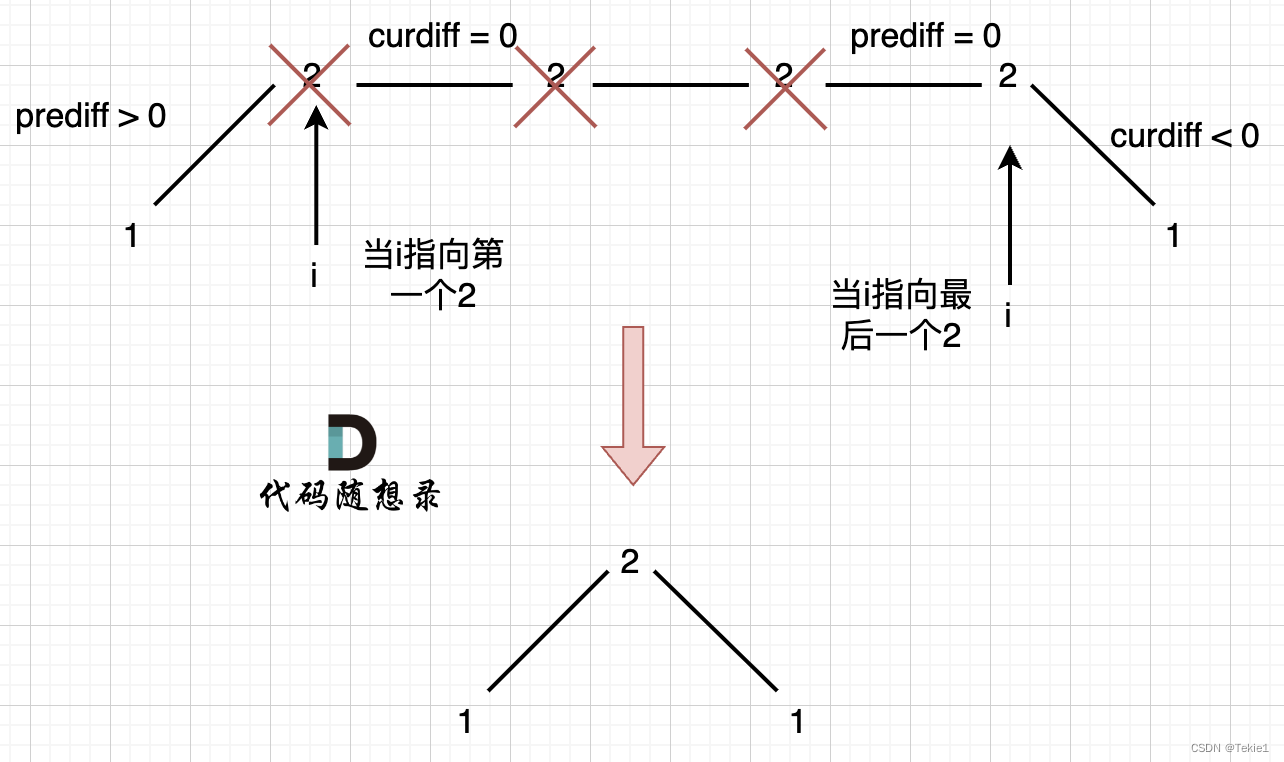
當 i 指向第一個 2 的時候，prediff > 0 && curdiff = 0 ，當 i 指向最后一個 2 的時候 prediff = 0 && curdiff < 0
當 prediff = 0 && curdiff < 0 也要記錄一個峰值，因為他是把之前相同的元素都刪掉留下的峰值。
所以我們記錄峰值的條件應該是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)
那么如果選擇保留第一個2，刪除其余2的時候，額外的判斷條件應該是prediff!=0 && curdiff=0

情況二：數組首尾兩端
對于左右端點的判斷情況
如果只有兩個不同的元素，那擺動序列也是 2
例如序列[2,5]，如果靠統計差值來計算峰值個數就需要考慮數組最左面和最右面的特殊情況。
左端點是沒有prediff的，右端點沒有curdiff,如果不需要寫if特判的話，那么我們需要假設左端點前面有一個虛擬端點，其值和左端點是一樣的，則左端點prediff=0

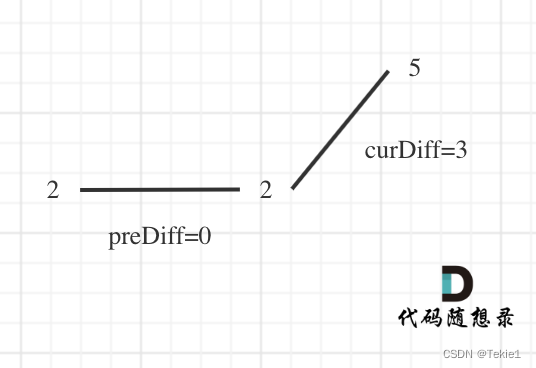
而對于右端點，我們直接假設其已經是一個峰值了（其必定為一個峰值，因為它是最后一個元素，可以畫圖想一下原理，要么就是極值，要么就是擺動的第一個元素），所以我們答案初始就為1
針對以上情形，result 初始為 1（默認最右面有一個峰值），對于左端點，此時 curDiff > 0 && preDiff <= 0，那么 result++（計算了左面的峰值），最后得到的 result 就是 2（峰值個數為 2 即擺動序列長度為 2）

情況三：單調坡中有平坡
我們忽略了一種情況，即 如果在一個單調坡度上有平坡

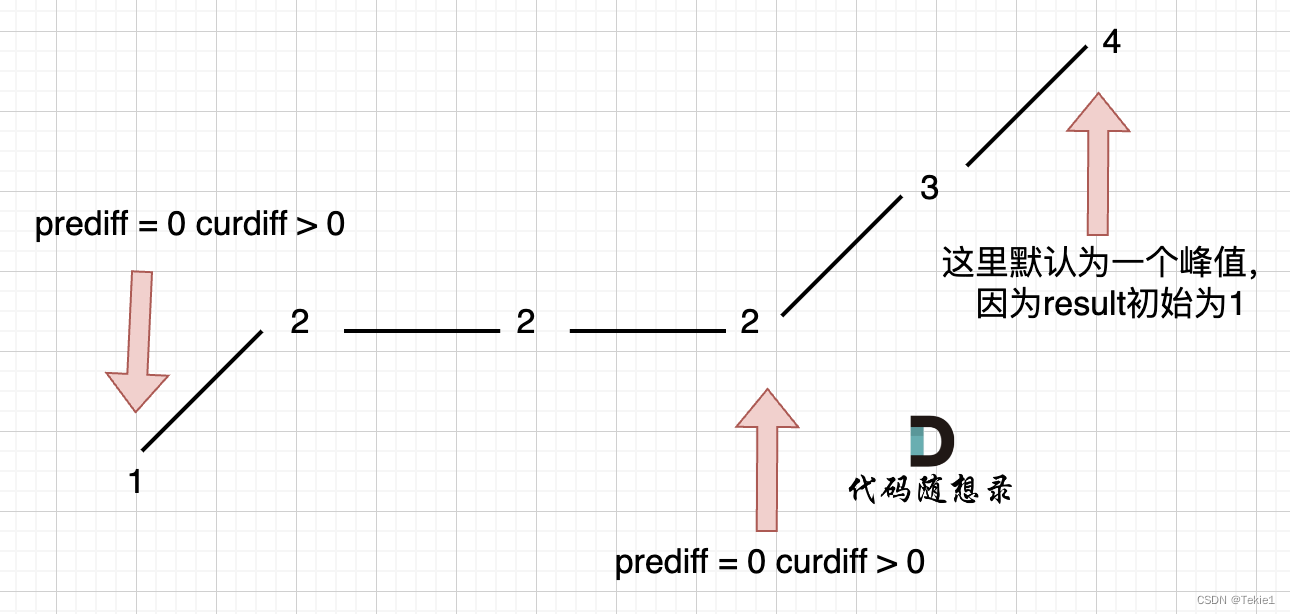
如果按照之前的條件
(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)
那么在最后一個2的時候，result就會+1，這明顯是不對的，因為答案應該為2->序列是[1,4]
之所以會出問題是因為prediff實時更新
我們應該在坡度變化的時候再用curdiff更新prediff，這樣它記錄了之前的坡度方向(大于0和小于0），這樣到1的時候prediff被更新為1，表示是一個上坡，然后坡度沒變化的時候prediff一直是1，到了最后一個2的時候prediff>0,curdiff>0,所以長度不會增加

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1)return nums.size();int curdif = 0;int predif = 0;int res = 1;for (int i = 0; i < nums.size() - 1; i++) {curdif = nums[i + 1] - nums[i];if ((predif <= 0 && curdif > 0) || (predif >= 0 && curdif < 0)) {res++;// 只有坡度變化才記錄predif = curdif;}}return res;}
};

53.最大子數組和

貪心
局部最優：當前“連續和”為負數的時候立刻放棄，從下一個元素重新計算“連續和”，因為負數加上下一個元素 “連續和”只會越來越小。

全局最優：選取最大“連續和”
局部最優的情況下，并記錄最大的“連續和”，可以推出全局最優。

從代碼角度上來講：遍歷 nums，從頭開始用 sum 累積，如果 sum一旦加上 nums[i]變為負數，那么就應該從 nums[i+1]開始從 0 累積 sum 了，因為已經變為負數的 count，只會拖累總和。

class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 1)return nums[0];int sum = 0;int res = -INT_MAX;for (int i = 0; i < nums.size(); i++) {if (sum <= 0)sum = 0;sum += nums[i];res = max(res, sum);}return res;}
};

用前綴和的做法也是可以的，用兩個變量
maxsum和minprefixsum來分別記錄遍歷到的最大子數組和以及最小前綴和
首先計算前綴和數組，sum[0] = 0
maxsum初始化為最小的int，minprefixsum初始化為0.
從前往后依次遍歷各個前綴和，記錄最大的前綴和之差，將其保存在maxsum，因為前綴和之差就是區間和
同時記錄最小的前綴和，因為一個后面的前綴和 sum[i]減去前面最小的前綴和minprefixsum,得到的一定是以當前數nums[i-1]為右端點的最大的區間和

class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 1)return nums[0];int n = nums.size();vector<int> sum(n + 1, 0);for (int i = 0; i < nums.size(); i++) {sum[i + 1] = sum[i] + nums[i];}int maxsum = INT_MIN;int minprefixsum = sum[0];for (int i = 1; i <= n; i++) {maxsum = max(maxsum, sum[i] - minprefixsum);minprefixsum = min(minprefixsum, sum[i]);}return maxsum;}
};