摘要

本研究提出了一種新的方法來重建代表大腦動力學的功能網絡，該方法基于兩個腦區在同一認知任務中的共同參與會導致其可識別性或其動力學特性降低的觀點。這種可識別性是通過深度學習模型在監督分類任務中獲得的分數來估計的，因此不需要對這種協同參與的性質進行先驗假設。該方法在阿爾茨海默病和帕金森病患者以及匹配的健康志愿者的睜眼和閉眼靜息態EEG信號上進行了測試，并通過標準拓撲度量對所得的功能網絡進行了分析。兩組患者都表現出相應腦電信號的可識別性降低，以及支持這種可識別性的模式存在差異。生成的功能網絡與使用相關性指標重建的功能網絡相似，但并非完全相同。控制組與患者之間的差異可以在不同網絡指標(如聚類系數和同配性)以及不同頻段中觀察到。睜眼和閉眼條件之間也存在顯著差異，特別是對于帕金森病患者。

引言

盡管經過了幾十年的實驗和理論研究，但在復雜認知任務甚至簡單的靜息態條件下，大腦活動背后的原理和機制仍然難以捉摸。提高我們對大腦理解的一個可能途徑是網絡神經科學，即通過網絡表征大腦活動，其中節點代表不同的大腦區域，并且每當檢測到相應區域之間存在信息傳播時，這些節點就會相互連接。這種方法具有整合性，因為元素根據它們的連接性進行表征，并將實證數據采集與計算方法相結合，因此該方法處于生物醫學和計算機科學的交叉領域。最重要的是，它對不同病理如何影響正常的大腦動態提供了開創性的見解。

這種網絡方法的一個基本假設是，兩個或多個腦區共同參與計算任務，導致相應腦區的動態具有一些共同的特征。換句話說，腦區在孤立狀態下具有獨特的動態，但通過參與任務(例如，通過共享一些信息)，這些不同的動態變得更加相似。通過線性相關性重建功能網絡就是一個最簡單的例子，預期不同腦區之間具有相關幅度，從而展現出共同的特征。當使用更復雜的指標時(比如因果關系或同步指標)，也會做出類似的假設。換句話說，重建功能網絡類似于檢測新出現的(廣義)相似性。

本文探討了一種相反的方法，即如何將認知任務的共同參與檢測為所涉及的大腦區域動態的獨特性下降。換句話說，類似于標準的功能網絡重建假設，本研究假設腦區在功能上是同質的，并且具有獨特的動力學特征；然而，在執行共同的認知任務時，這種獨特性在一定程度上會減弱。因此，本研究不再專注于檢測相似性的增加，而是將焦點轉向獨特性的減少。這種方法遠非單純的語義轉換，它具有兩個重要優勢。首先，它不對腦區動力學的共同特征做出假設，比如相關性、相位等等。相反，任何能夠減少動力學獨特性的共同特征都會被考慮在內，前提是我們有方法來檢測這種減少。其次，這種方法可以被定義為一種分類任務，即訓練一個機器學習模型來識別來自兩個腦區記錄的時間序列；分類得分越高，兩個區域就越獨特(或可識別)，因此它們參與相同認知任務的次數就越少。這使我們能夠借助深度學習(DL)模型，即最先進的機器學習算法，無需假設或數據先驗結構，而且非常敏感，能夠檢測數據集之間微妙而復雜的差異。

雖然DL模型在神經科學領域并不陌生，但本研究方法在兩個主要方面有所不同。首先，分類模型并不用于實際分類。相反，分類任務的得分用于評估每組數據的獨特性，也就是其可識別性。其次，分類的結果并非孤立使用，而是基于網絡表征的更復雜分析中的一步。因此，分類不是目的，而是分析的工具。通過將該方法應用于帕金森病(PD)和阿爾茨海默病(AD)患者以及對照組的EEG靜息態記錄數據集，探討了這種方法的可能性和局限性。

材料與方法

參與者

本研究招募了50名參與者，根據其健康狀況分為三組：阿爾茨海默病(AD)和帕金森病(PD)患者，以及健康的老年對照組。參與者的人口統計信息如表1所示。所有參與者均接受完整的神經系統檢查、結構磁共振成像(MRI)、常規實驗室篩查以及一系列神經心理學測試。

表1.人口統計信息。

EEG數據記錄

使用Brain Products BrainAmp 32通道DC系統記錄EEG數據，采樣率為500Hz。使用EasyCap與32 Ag/AgCl電極按10/20系統放置，所有電極阻抗均保持在10kΩ以下。使用A1和A2電極作為參考電極(耳垂)。為了記錄眼電圖(EOG)，使用了兩個Ag/AgCl電極，分別放置在左眼眶上緣和外側緣。所有被試的EEG記錄包含4分鐘的睜眼和4分鐘的閉眼數據(即每個被試的每個通道約有240000個數據點)。在睜眼記錄期間，要求被試注視黑屏。在整個EEG記錄期間，研究人員使用攝像頭對被試進行監測。

用于時間序列分類的深度學習模型

本研究重點關注時間序列分類模型，即給定一組時間序列，每個序列都有一個標簽(即它所對應的EEG通道)，目標是為呈現給算法的新時間序列分配正確的標簽。文獻中已經提出了幾種用于這一任務的模型，通常由圖像分類模型演變而來(有關完整的綜述和相應的源代碼，請參閱https://github.com/hfawaz/dl-4-tsc)。更具體地說，使用了以下五種模型。

多層感知器(MLP)。它是神經網絡最傳統和最簡單的形式之一，由一組按層組織的節點組成，每個節點從前一層接收信息，并通過非線性激活函數做出響應。盡管MLP模型不編碼時間信息，但它已被提出作為時間序列分類的基準架構。這里考慮的網絡由四層組成，每層都與前一層的輸出完全連接，最后一層是softmax分類器。激活函數是眾所周知的整流線性單元(ReLU)。

卷積神經網絡(CNN)。卷積網絡是MLP的變體，其中矩陣乘法用卷積運算代替。它們的優點包括空間(或者在時間序列情況下，時間)不變性，以及減少過擬合的傾向。在這里，本研究采用一個簡單的卷積模型，包括兩個卷積層和一個Sigmoid分類器。

殘差網絡(ResNet)。殘差網絡的靈感來自大腦皮層中錐體細胞的組織方式；具體而言，層與層之間的連接不是連續的，而是可以跳過某些層。這樣做的好處是簡化了結構，因此減少了訓練成本。這里考慮的網絡由11個層組成，前9層是卷積層，然后是一個全局平均池化層，該層對整個時間維度的時間序列進行平均，最后是一個softmax分類器。

全卷積神經網絡(FCN)。FCNs是一種只執行卷積運算的網絡。該模型由三個卷積塊組成，每個塊都執行卷積、批量歸一化和激活。最后，第三個卷積塊的結果被輸入到softmax分類器中。

多通道深度卷積神經網絡(MCDCNN)。該模型是基于改進的CNN，其中卷積獨立地(并行地)應用于輸入多變量時間序列的每個維度(或通道)。由于這里只考慮單變量數據，即每個EEG通道由單個時間序列表示，因此MCDCNN和CNN的結果雖然并不總是相同，但可能會相似。

分類任務和可識別性

給定同一組中(對照組、阿爾茨海默病和帕金森病患者)所有被試的一對EEG通道的時間序列，通過DL模型的最佳分類分數對這兩個通道的可識別性進行評估。在分類問題的每次迭代中，時間序列被分成1000個數據點的非重疊段(相當于2s)。可用時間序列的隨機一半用于訓練，剩下的一半用于模型評估，因此相當于二折交叉驗證。最終通過相應的準確率分數來衡量每個模型的性能，即正確分類片段所占的比例；需要注意的是，由于使用了完全平衡的數據集，其他指標(例如召回率或F分數)在這里是多余的。為了清晰起見并避免與同名的復雜網絡指標混淆，這里將效率稱為分類分數，或者在簡稱為分數。

功能網絡重建與分析

在復雜網絡理論中，一個網絡由大小為N×N(其中N為節點數)的鄰接矩陣A定義，其中元素ai,j在連接節點i和j時設為1，否則設為0。在網絡神經科學背景下，當傳感器i和j對應的時間序列之間計算得到的同步指標(例如，相關性)大于給定閾值時，ai,j被設置為1，這表明存在一種共享的動態。如前所述，這里提出的方法是相反的：由于共享動態會導致這兩個傳感器的可識別性降低，因此當這種可識別性(通過相應的分類分數來衡量)低于閾值時，將添加一個連接。也就是說，分類分數越低，相應腦區之間的連接就越強。

一旦這些網絡被重建，它們就會被二值化，也就是說，強度超過給定閾值的連接將被保留，其他的則被刪除。這是網絡神經科學中的一種標準方法，可以減少弱連接的影響。本文采用一種比例閾值法，在每個網絡中包含固定數量的最強連接。這種方法通常被稱為密度或網絡成本保持不變的分析，并被認為有利于病例對照研究。

結果

比較DL模型

首先通過比較不同深度學習模型獲得的分數來分析結果；如前所述，這些模型基于不同的架構并檢測數據中的不同模式，因此預計它們會產生異質的結果。對于三組被試，圖1報告了每對EEG通道中獲得最佳分數的模型。可以看出，模型以非隨機方式分布，一些模型與某些腦區的較高分數相關。不同腦區具有不同的活動模式，這些模式更容易被某些模型識別。此外，三組之間存在差異，表明兩種病理情況進一步改變了局部動態。

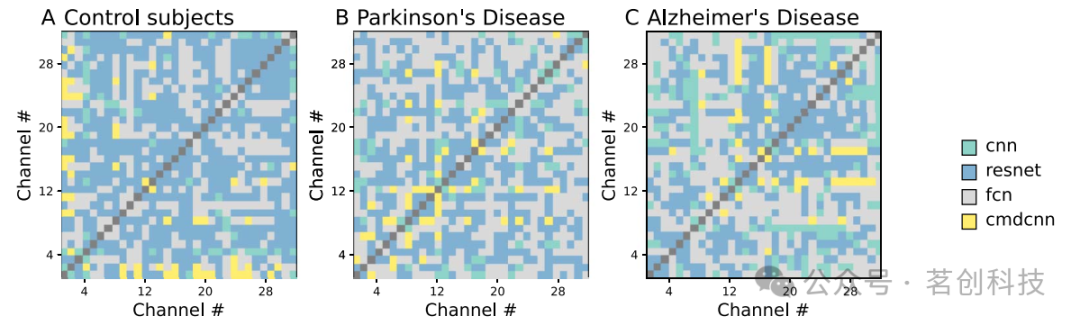
圖1.四種DL模型的比較。

EEG通道對的可識別性

然后分析了每對EEG通道的可識別性。具體來說，圖2頂部的三個圖顯示了每對通道在三組中獲得的平均分類分數。請注意，在本文的其余部分，對于給定的EEG通道對，所報告的分類分數與最佳DL模型產生的分數相對應。結果表明，三組中的連接性共享相同的基礎結構，并且受到傳感器之間串擾的強烈影響。為了突出與條件相關的模式，底部的三個圖顯示了每對條件之間(兩組之間)在通道對上的可識別性差異。這種差異主要表現為一些特定的EEG通道中存在的模式。總的來說，與對照組相比，AD患者的可識別度明顯降低；在PD患者中，下降程度相對較輕。

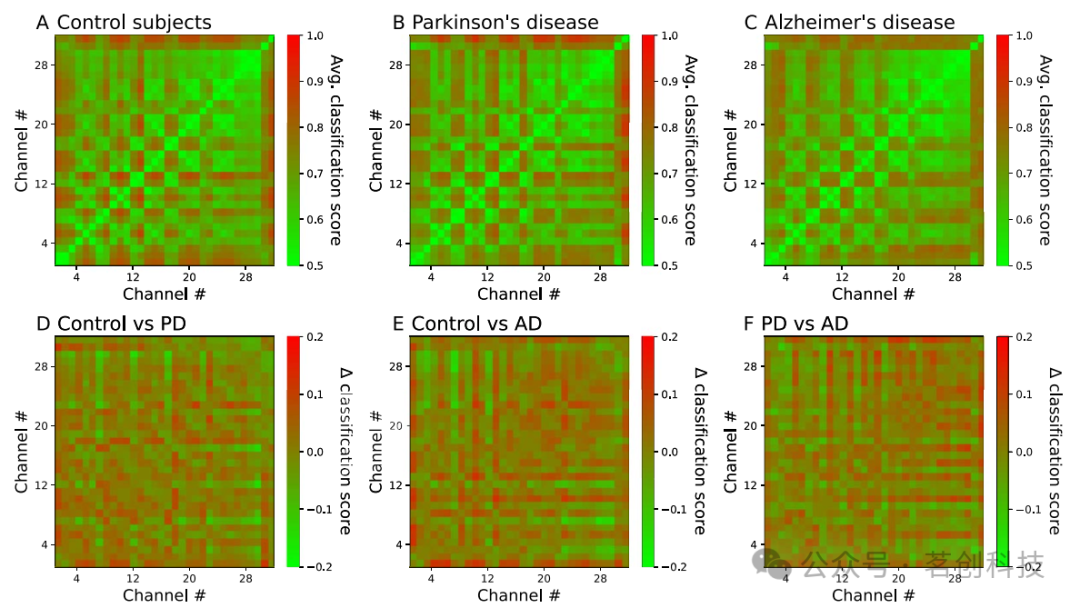
圖2.EEG通道對的可識別性。

本研究進一步分析了這種成對可識別性的另外兩個方面。首先，人們可能會問，可識別性(這里定義為分類任務產生的分數)與更傳統的功能指標之間有什么關系。為了回答這個問題，圖3報告了三個散點圖(每個條件一個散點圖)，即每對EEG通道之間的Pearson線性相關性的平均絕對值，作為相應分類分數的函數。正如預期的那樣，可以觀察到普遍的負相關；換言之，高度相關的通道由于動態相似而更難被識別，從而具有較低的可識別性。然而，這兩個指標并不相同；弱相關的時間序列可以產生高和低的分類分數，這表明深度學習模型可以檢測到更復雜的模式。舉例來說，如果兩個時間序列具有相似的動態特性但具有不同的特征頻率，即使它們的相關性很低，它們也很容易被識別。另一方面，兩個非常復雜的時間序列也可能是弱相關的，并且識別其獨特模式也將是一項具有挑戰性的任務。

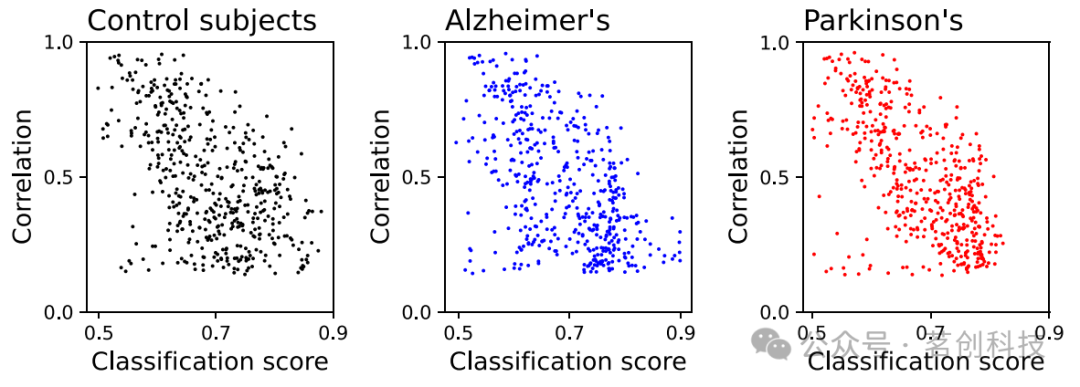
圖3.線性相關與分類分數。

其次，本研究分析了時間序列的可識別性與頻率信息的關系。具體而言，在圖4的頂圖中報告了每種條件的分類分數直方圖，以及寬頻信號和四個濾波頻段：α(8-13Hz)、β1(13-20Hz)、β2(20-30Hz)和γ(30-50Hz)。此外，該圖的底圖報告了三種條件和五個頻段的中位分類分數。寬帶時間序列始終更容易被識別；每種條件下都可以觀察到一些細微差異，例如，PD患者和β2頻段的可識別度下降。

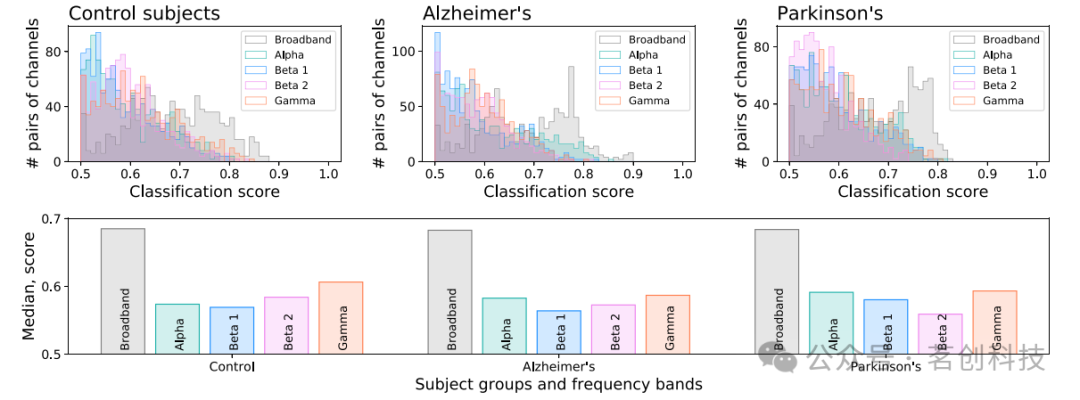
圖4.可識別性和頻率信息。

網絡分析

重建功能網絡的常用方法包括對EEG信號對進行成對比較，從而得到每個被試的功能網絡。然后，可以對這些網絡，以及從這些網絡中提取的拓撲指標，在多個患者之間進行平均，以獲得給定條件的全局圖像。α頻段和β1頻段的聚類系數，以及寬頻信號和β1頻段的同配性如圖5所示。為了評估這些結果的顯著性，灰色區域報告了相同指標在10-90百分位數范圍內的數值，基于所有三組時間序列的功能網絡重建的零模型獲得；每個子圖內的插圖進一步報告了每組指標的Z分數(根據該零模型計算得出)隨時間的變化情況。從圖中還可以觀察到各組之間的一些差異。例如，AD組在α頻段的聚類系數更高，但在β1頻段較低；相比于PD，AD在寬頻信號和β1頻段上具有更大的同配性。

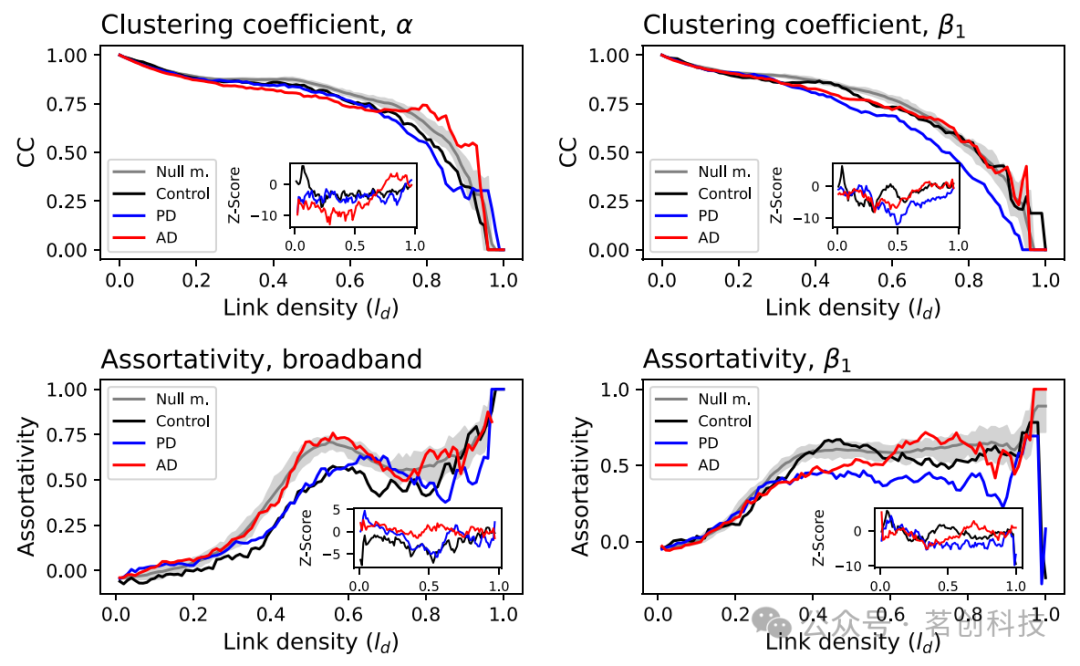
圖5.拓撲指標示例。

本研究進一步分析了這些拓撲指標如何受到被試者睜眼或閉眼狀態的影響。圖6說明了兩個拓撲指標的演變情況；頂圖對應于原始指標數值，而底圖對應于使用零模型計算的Z分數，即與圖5中的插圖相同。可以觀察到一些大致趨勢，比如PD患者閉眼和AD患者睜眼的差異較大：前者(后者)的聚類系數和同配性最小(最大)，但嵌套性最大(最小)。

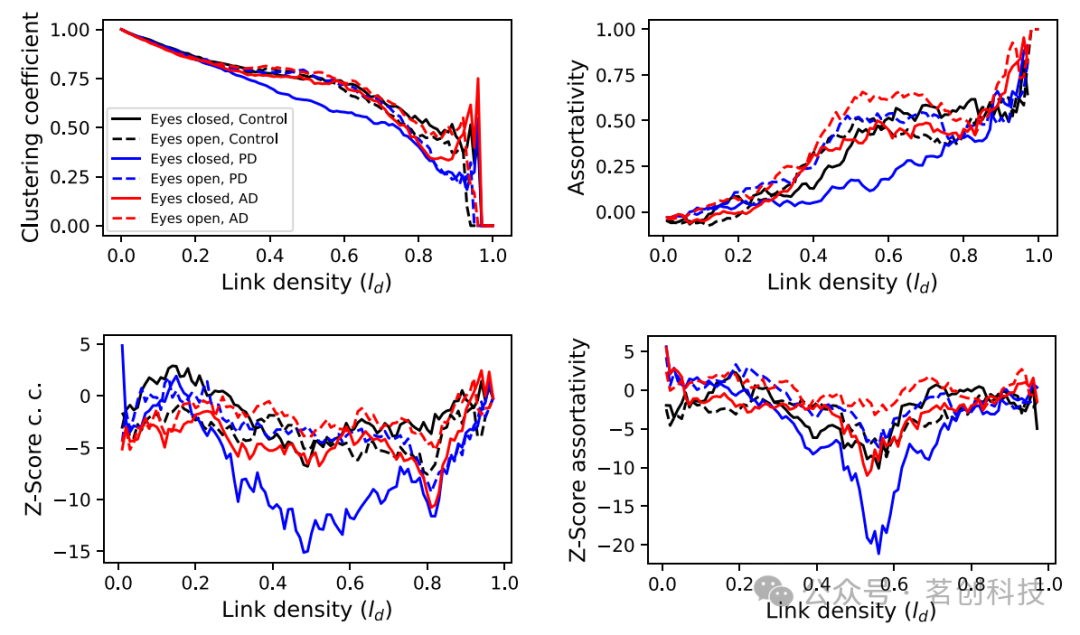
圖6.睜眼和閉眼條件的比較。

結論

本研究提出了一種分析神經影像信號的新方法，該方法基于對每個腦區動態的可識別性或“獨特性”的評估。這種方法無需先驗地假設必須分析時間序列的哪些方面來檢測相似性，而是關注使時間序列(或一組時間序列)具有獨特性的任何動態方面。這使我們能夠借助深度學習(即最先進的機器學習模型)進行分析。最終結果可用于檢測認知任務中腦區協同參與所導致的動力學損失，從而為重建腦功能網絡提供一種新的方法。

參考文獻：Zanin, M., Aktürk, T., Y?ld?r?m, E., Yerlikaya, D., Yener, G., & Güntekin, B. (2024). Reconstructing brain? functional networks through? identifiability and deep learning. Network Neuroscience, 8(1), 241–259. https://doi.org/10.1162/netn_a_00353

?小伙伴們關注茗創科技，將第一時間收到精彩內容推送哦～