?大俠幸會，在下全網同名[算法金] 0 基礎轉 AI 上岸，多個算法賽 Top [日更萬日，讓更多人享受智能樂趣]

1. 引言

數據分析中聚類算法的作用

在數據分析中，聚類算法用于發現數據集中的固有分組，通過將相似對象聚集在一起來揭示數據的結構和模式。這種方法常用于市場細分、社交網絡分析、組織復雜數據集等領域。

選擇K-Means聚類算法的動機

K-Means 是一種廣泛使用的聚類算法，主要因其簡單、高效，適用于大規模數據處理。它通過優化簇內距離來形成相對均勻的簇，適合于許多實際應用中的基本聚類需求。

K-Means聚類算法的簡述

K-Means 是一個無監督學習算法，它的目標是將 n 個觀測值劃分到 k 個簇中，使得每個觀測值屬于離它最近的簇中心（質心），從而使簇內的方差最小。

2. K-Means聚類算法概述

2.1 監督學習與無監督學習的對比

監督學習需要預先標記的輸出結果來訓練模型，常用于分類和回歸任務。無監督學習不依賴于標注輸出，而是通過分析數據的內在結構和關系來學習數據的分布或模式，聚類是無監督學習中的典型例子。

2.2 K-Means算法簡介

K-Means算法通過迭代過程選擇簇中心和劃分簇來優化簇內距離，直到達到最優或滿足停止條件。該算法只需要指定簇的數量 k，并對初始簇中心的選擇敏感。

2.3 K-Means的應用實例

K-Means廣泛應用于客戶細分、圖像分割、文檔聚類等多個領域，通過識別相似特征的聚集，幫助企業或研究者洞察數據特征和群體行為。

3. K-Means算法的工作原理

3.1 簇與質心的定義

在 K-Means 算法中，"簇"是數據點的集合，這些數據點彼此之間比與其他簇的數據點更相似。"質心"是簇內所有點的平均位置，代表了簇的中心。

3.2 算法步驟詳解

K-Means算法的基本步驟包括隨機初始化質心，計算每個數據點到每個質心的距離，根據最近質心重新分配數據點到簇，重新計算簇的質心，重復這一過程直到質心不再變化或達到預定的迭代次數。

3.3 初始質心選擇的重要性及其影響

初始質心的選擇可能會極大影響算法的收斂速度和最終聚類的質量。不恰當的初始質心可能導致簇結果不穩定或收斂到局部最優。

4. K-Means算法的數學基礎

4.1 簇內誤差平方和的計算及其評估作用

簇內誤差平方和（SSE）是衡量聚類效果的一個重要指標，計算方法是將簇內每個點到其質心的距離平方求和。優化目標是最小化 SSE，從而提高簇的緊密性。

4.2 不同距離度量方法的比較

K-Means常用歐氏距離作為距離度量，但在不同的應用場景中，可以考慮曼哈頓距離、余弦相似度等其他度量方法，以更好地適應數據特性。

5. K-Means算法的實現

5.1 使用Python及scikit-learn實現K-Means

Python 的 scikit-learn 庫提供了 K-Means 算法的高效實現。以下是使用 scikit-learn 實現 K-Means 的基本代碼示例：

from sklearn.cluster import KMeans
import numpy as np
# 生成模擬數據
X = np.random.rand(100, 2)
# 初始化 KMeans
kmeans = KMeans(n_clusters=3)
# 擬合模型
kmeans.fit(X)
# 獲取簇標簽
labels = kmeans.labels_

5.2 算法的初始化策略

scikit-learn 中的 K-Means 實現支持多種初始化策略，如隨機初始化和 K-Means++ 初始化，后者可以優化初始質心的選擇，提高算法的穩定性和效率。

5.3 迭代過程與收斂條件

K-Means 算法的迭代繼續進行，直到質心的更新非常小（在設定的閾值之下）或達到預設的迭代次數。這確保了算法能夠在合理的時間內收斂到一個穩定的簇劃分。

6. 模型評估與選擇K值

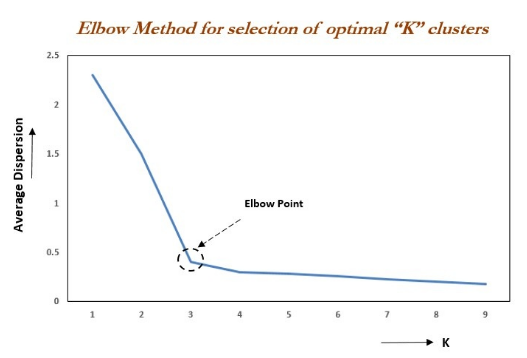
6.1 手肘法的原理與應用

手肘法是一種用來選擇 K 值的技術，它通過繪制不同 K 值的 SSE 曲線，尋找曲線的“手肘”點，即 SSE 下降速度顯著變緩的點，通常認為這一點是最佳的簇數量。

6.2 輪廓系數的計算與意義

輪廓系數衡量了簇內的緊密性和簇間的分離度，值范圍從 -1 到 1。較高的輪廓系數表明簇內部的點相互更接近，而與其他簇的點較遠離，反映了聚類的效果較好。

6.3 確定K值的其他方法

除手肘法和輪廓系數外，還可以通過交叉驗證、信息準則如 AIC 或 BIC 以及實際應用需求來確定最佳的 K 值。

7. K-Means算法的優缺點

7.1 算法的優勢分析

K-Means 算法簡單、易于實現，計算效率高，尤其適用于處理大規模數據集。這使得它成為實際應用中最常用的聚類算法之一。

7.2 算法的局限性討論及問題解決方案

K-Means的主要局限性包括對初始質心選擇敏感、對噪聲和異常值較為敏感、只能處理球形簇等。針對這些問題，可以采取諸如數據預處理、使用 K-Means++ 初始化等策略來改善算法性能。

8. K-Means算法的變體與改進

8.1 K-Means++算法介紹

K-Means++ 是對傳統 K-Means 算法的一項重要改進，通過一種特定的概率方法來選擇初始質心，可以顯著提高聚類的質量和算法的收斂速度。

8.2 針對不同數據集的優化策略及案例分析

為了應對不同類型的數據集和特定的應用場景，K-Means 算法被適當修改和優化。例如，使用加權距離度量在處理非均勻特征的數據集時，或者調整算法參數以適應高維數據。

9. K-Means在文本聚類中的應用

9.1 文本數據的預處理與向量化

文本聚類前的預處理包括清洗文本、分詞、去除停用詞等步驟。向量化通常通過 TF-IDF 方法實現，它幫助轉換文本數據為算法可處理的數值型特征。

9.2 K-Means與TF-IDF的結合應用

結合 K-Means 算法和 TF-IDF 向量化的方法在文本聚類中廣泛應用，有效地將相關文檔聚集在一起，便于后續的文本分析和信息檢索。

9.3 文本聚類的實際案例分析

案例分析可以展示 K-Means 算法在文本聚類中的應用效果，如新聞文章分類、社交媒體帖子分析等，展示如何從大量文本中提取有用信息。

[ 抱個拳，總個結 ]

K-Means 是一種強大而靈活的聚類工具，盡管它有一些局限性，但正確使用時，它能有效地組織大規模數據集，揭示隱藏的模式和群體結構，是數據分析不可或缺的工具。