后端分類

1. 基于濾波器的后端。常見的擴展卡爾曼EKF，無跡卡爾曼UKF，粒子濾波PF，或者是fastlio2中使用的誤差狀態卡爾曼ESIKF（本質上迭代過程等效于高斯牛頓法，優化當前幀的狀態）。還有許多其他濾波器，本質上是基于一階馬爾可夫性假設，就是認為當前的狀態$x_k$只與$x_{k?1}$有關，與歷史之前的狀態無關，來簡化卡爾曼濾波過程中預測更新的運算。
2. 基于非線性優化的后端。這種方法就可以考慮第k幀之前所有歷史幀的狀態，類似一個全局的思維，通過構建全局狀態的優化問題，來優化所有幀的狀態（包括位姿和特征點），特別能夠依靠回環檢測來提高狀態的全局一致性。
3. 滑動窗口濾波和優化。
   （1）滑動窗口濾波其實應該就是基于濾波器的后端的一個變種，認為一階馬爾可夫性假設太極端了，所以想選擇一定數量的關鍵幀，共同考慮多個幀去解算出當前幀的狀態。
   （2）滑動窗口優化應該也是基于非線性優化的后端的一個變種，認為隨著SLAM過程，關鍵幀增多，優化耗時會增加，所以想選擇一些離當前時刻接近的關鍵幀而不是全部關鍵幀來一起優化

基于濾波器的后端

這里首先將狀態的符號簡化，狀態包含相機位姿（$x_k$）和特征點（$y_m$）。
x k = def? { x k , y 1 , … , y m } \boldsymbol{x}_k \stackrel{\text { def }}{=}\left\{\boldsymbol{x}_k, \boldsymbol{y}_1, \ldots, \boldsymbol{y}_m\right\} xk?=?def?{xk?,y1?,…,ym?}
那么經典的運動和觀測方程就可以簡化：（注意狀態上的符號，$\hat{\mathbf{x}}$代表狀態的后驗，$\check{\mathbf{x}}$代表狀態的預測，這個定義是為了跟slam14講ppt里一致）
$$\{\begin{array}{l}{\mathbf{x}}_k=f\left({\hat{\mathbf{x}}}_{k?1},{\mathbf{u}}_k\right)+{\mathbf{w}}_k\\ {\mathbf{z}}_k=h\left({\mathbf{x}}_k\right)+{\mathbf{v}}_k\end{array}k=1,\dots ,N$$
我們已知的是k-1時刻狀態的后驗${\hat{x}}_{k?1}$和輸入$u_k$，想求的是當前k時刻狀態${\hat{x}}_k$的后驗分布
$$P\left({\hat{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k}\right)$$
根據貝葉斯法則，書上給出的式子是這樣的：
$$P\left({\hat{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\check{\mathbf{x}}}_k\right)P\left({\check{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k?1}\right)$$

但是在我看來，假設了一階馬爾可夫性，直接都可以簡化成最基本的貝葉斯濾波的形式。
$$P\left({\hat{\mathbf{x}}}_k\mid {\hat{\mathbf{x}}}_{k?1},{\mathbf{u}}_k,{\mathbf{z}}_k\right)\propto P\left({\mathbf{z}}_k\mid {\check{\mathbf{x}}}_k\right)P\left({\check{\mathbf{x}}}_k\mid {\hat{\mathbf{x}}}_{k?1},{\mathbf{u}}_k\right)$$
很明顯上面式子中左邊的是當前k時刻狀態${\hat{x}}_k$的后驗分布，右邊的第一項是似然分布，第二項是預測即先驗分布。因為后驗分布、似然分布和先驗分布都屬于高斯分布，所以就可以通過經典的卡爾曼濾波公式來求當前k時刻狀態${\hat{x}}_k$的后驗分布。

線性系統和卡爾曼濾波

如果考慮線性系統，那就是經典的卡爾曼濾波系統。運動方程和觀測方程可以由下面的式子表示：
$$\{\begin{array}{l}{\mathbf{x}}_k={\mathbf{A}}_k{\mathbf{x}}_{k?1}+{\mathbf{u}}_k+{\mathbf{w}}_k\\ {\mathbf{z}}_k={\mathbf{C}}_k{\mathbf{x}}_k+{\mathbf{v}}_k\end{array}k=1,\dots ,N$$
其中過程噪聲${\mathbf{w}}_k～N(0,\mathbf{R})$ 和觀測噪聲${\mathbf{v}}_k～N(0,\mathbf{Q})$ 都服從高斯分布。然后就是根據卡爾曼濾波的5個步驟，求出后驗估計${\hat{x}}_k$。
$${\check{\mathbf{x}}}_k={\mathbf{A}}_k{\hat{\mathbf{x}}}_{k?1}+{\mathbf{u}}_k\text{\hspace{1em}(1)}$$

$${\check{\mathbf{P}}}_k={\mathbf{A}}_k{\hat{\mathbf{P}}}_{k?1}{\mathbf{A}}_k^{\mathrm{T}}+\mathbf{R}\text{\hspace{1em}(2)}$$

$$\mathbf{K}={\check{\mathbf{P}}}_k{\mathbf{C}}_k^{\mathrm{T}}{\left({\mathbf{C}}_k{\check{\mathbf{P}}}_k{\mathbf{C}}_k^{\mathrm{T}}+{\mathbf{Q}}_k\right)}^{?1}\text{\hspace{1em}(3)}$$

$${\hat{\mathbf{x}}}_k={\check{\mathbf{x}}}_k+\mathbf{K}\left({\mathbf{z}}_k?{\mathbf{C}}_k{\check{\mathbf{x}}}_k\right)\text{\hspace{1em}(4)}$$

$${\hat{\mathbf{P}}}_k=\left(\mathbf{I}?\mathbf{K}{\mathbf{C}}_k\right){\check{\mathbf{P}}}_k\text{\hspace{1em}(5)}$$

于是這就得到了后驗${\hat{x}}_k$的均值和協方差，用于k+1時刻的預測。

非線性系統和擴展卡爾曼濾波

本質上是在卡爾曼濾波基礎上對運動方程和觀測方程進行線性化（一階泰勒展開），在此基礎上也是經過5個公式推出$x_k$的后驗分布。這里就不展開了，公式都是大同小異。

BA優化

主要就是通過Bundle Adjustment（BA），來構建最小二乘問題，通過非線性優化的方法優化相機位姿和特征點的位置。
下面這個圖就很好描述了相機的觀測方程：

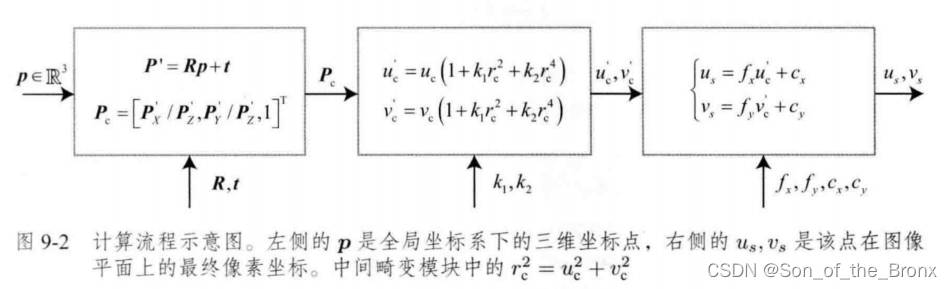
然后就是根據其他時刻的相機與特征點，構建出全局的重投影誤差
$$\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{e}}_{ij}\Vert }^2=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{z}}_{ij}?h\left({\mathbf{T}}_i,{\mathbf{p}}_j\right)\Vert }^2$$
其中i是相機位姿的序號，j就是相機位姿i看到的特征點。
為了優化這個目標函數，需要求目標函數對相機位姿和特征點的雅可比，然后通過高斯牛頓來優化相機位姿和特征點：
$$\frac{1}{2}\Vert f(\mathbf{x}+\Delta \mathbf{x}){\Vert }^2\approx \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{e}}_{ij}+{\mathbf{F}}_{ij}\Delta {\mathbf{\xi }}_i+{\mathbf{E}}_{ij}\Delta {\mathbf{p}}_j\Vert }^2$$
其中狀態x定義成所有待優化的變量：
$$\mathbf{x}={\left[{\mathbf{T}}_1,\dots ,{\mathbf{T}}_m,{\mathbf{p}}_1,\dots ,{\mathbf{p}}_n\right]}^{\mathrm{T}}$$
${\mathbf{F}}_{ij}$和${\mathbf{E}}_{ij}$分別是誤差對相機位姿和特征點的偏導。
最后的優化問題也可以簡化成：
$$\frac{1}{2}\Vert f(\mathbf{x}+\Delta \mathbf{x}){\Vert }^2=\frac{1}{2}{\Vert \mathbf{e}+\mathbf{F}\Delta {\mathbf{x}}_c+\mathbf{E}\Delta {\mathbf{x}}_p\Vert }^2$$
最后根據高斯牛頓法，都是需要求解一個增量方程
$$\mathbf{H}\Delta \mathbf{x}=\mathbf{g}$$
對于高斯牛頓法，H矩陣就是
$$\mathbf{H}={\mathbf{J}}^{\mathrm{T}}\mathbf{J}=\left[\begin{array}{ll}{\mathbf{F}}^{\mathrm{T}}\mathbf{F}& {\mathbf{F}}^{\mathrm{T}}\mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}\mathbf{F}& {\mathbf{E}}^{\mathrm{T}}\mathbf{E}\end{array}\right]$$

實際上這個H矩陣由于特征點的個數往往很多，所以H矩陣規模很大，直接求逆會很耗時，但是H矩陣是有一定的結構，利用這個結構可以加速優化過程。

H矩陣的稀疏性和邊緣化

首先這里書本舉一個例子說明：

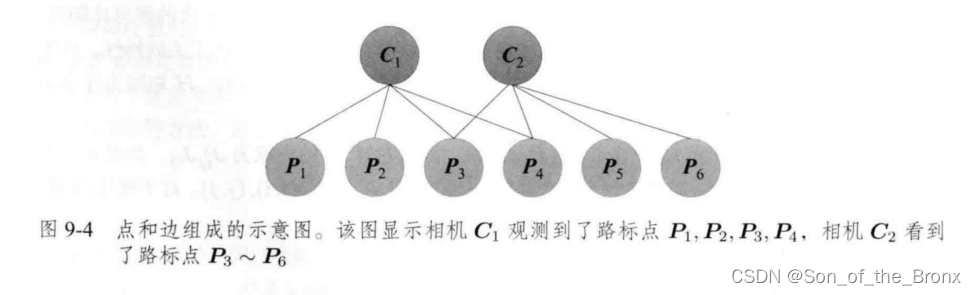
其中圖中有$C_1$和$C_2$兩個相機位姿和六個特征點，連線代表有觀測關系。
這時全局重投影的目標函數為
$$\frac{1}{2}\left({\Vert {\mathbf{e}}_{11}\Vert }^2+{\Vert {\mathbf{e}}_{12}\Vert }^2+{\Vert {\mathbf{e}}_{13}\Vert }^2+{\Vert {\mathbf{e}}_{14}\Vert }^2+{\Vert {\mathbf{e}}_{23}\Vert }^2+{\Vert {\mathbf{e}}_{24}\Vert }^2+{\Vert {\mathbf{e}}_{25}\Vert }^2+{\Vert {\mathbf{e}}_{26}\Vert }^2\right)$$
首先以$e_{11}$對狀態x求偏導，可以得到下面的雅可比

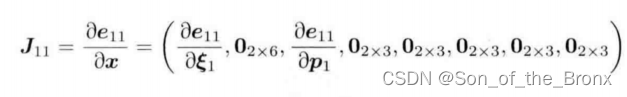
同理其他誤差的雅可比都會有這種形式：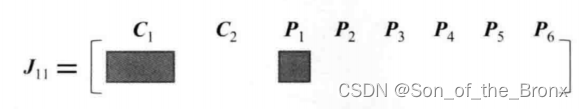
整體的雅可比J和H矩陣就會如同下圖所示

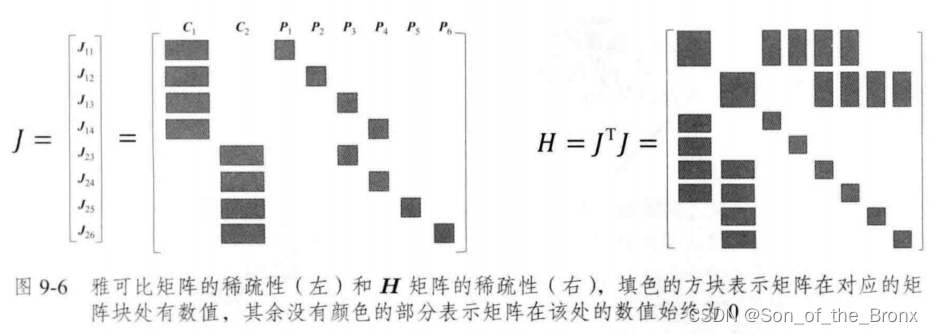
然后對H矩陣進行下圖的劃分：

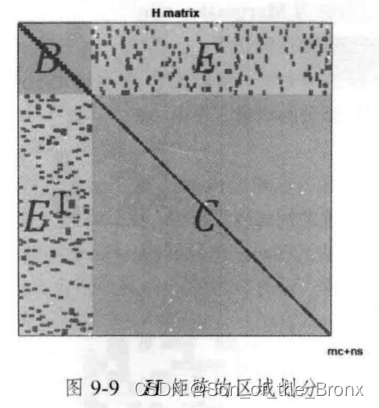
增量方程也可以按照劃分，變成下面的形式
$$\left[\begin{array}{ll}\mathbf{B}& \mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{l}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{l}\mathbf{v}\\ \mathbf{w}\end{array}\right]$$

對這個線性方程組的求解可以通過邊緣化（可通過schur消元進行邊緣化，也就是書中的方法。當然也有其他方法進行邊緣化，本質都是加快增量方程的求解速度）。邊緣化的過程如下：
$$\left[\begin{array}{cc}\mathbf{I}& ?\mathbf{E}{\mathbf{C}}^{?1}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}\mathbf{B}& \mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{c}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{cc}\mathbf{I}& ?\mathbf{E}{\mathbf{C}}^{?1}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{c}\mathbf{v}\\ \mathbf{w}\end{array}\right]$$
最終整理得到：
$$\left[\begin{array}{cc}\mathbf{B}?\mathbf{E}{\mathbf{C}}^{?1}{\mathbf{E}}^{\mathrm{T}}& 0\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{l}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{c}\mathbf{v}?\mathbf{E}{\mathbf{C}}^{?1}\mathbf{w}\\ \mathbf{w}\end{array}\right]$$
因為右上角為0，就可以先把$\Delta {\mathbf{x}}_{\mathrm{c}}$計算出來，因為c是對角塊矩陣，所以它的求逆相對簡單。將求出$\Delta {\mathbf{x}}_{\mathrm{c}}$后再帶入原方程就可以解出$\Delta {\mathbf{x}}_{\mathrm{p}}$。

H矩陣求解的總結

這個邊緣化的概念是從概率論的角度來看的。實際上這個求解步驟就是固定$\Delta {\mathbf{x}}_{\mathrm{p}}$，然后求解$\Delta {\mathbf{x}}_{\mathrm{c}}$，最后再算出$\Delta {\mathbf{x}}_{\mathrm{p}}$。從概率公式上：
$$P\left({\mathbf{x}}_{\mathrm{c}},{\mathbf{x}}_p\right)=P\left({\mathbf{x}}_{\mathrm{c}}\mid {\mathbf{x}}_p\right)P\left({\mathbf{x}}_p\right)$$
最終是求得了${\mathbf{x}}_{\mathrm{c}}$的條件概率分布，和${\mathbf{x}}_{\mathrm{p}}$的邊緣分布，所以稱邊緣化。在消元的時候實際上是將特征點的部分信息融入了求解${\mathbf{x}}_{\mathrm{c}}$的過程，所以${\mathbf{x}}_{\mathrm{c}}$是條件概率分布。

需要注意的是，這個邊緣化在滑動窗口的方法中也有所應用。

位姿圖優化

位姿圖優化在視覺SLAM中可以看成是BA優化的簡化版。因為BA優化需要將特征點考慮進去，優化的變量包括相機位姿和特征點的位置，大部分是放在特征點優化上了，所以位姿圖的意義在于構建一個只有軌跡的圖優化問題，特征點看成是一幀相機位姿中確定的點，不再去優化特征點的位置，省去了大量特征點優化的計算。

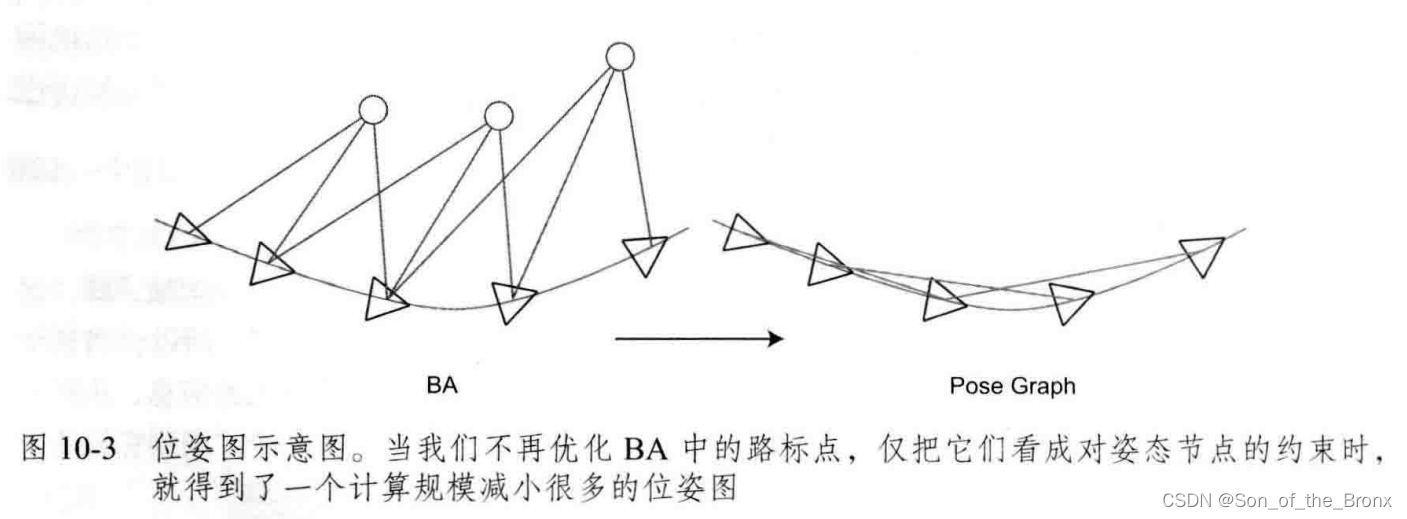
公式推導

假設通過IMU積分或者視覺slam估計了$T_i$和$T_j$之間的一個運動$\Delta {\mathbf{T}}_{ij}$，然后取他們李群之間的差值對應的李代數為誤差：
$${\mathbf{e}}_{ij}=\Delta {\mathbf{\xi }}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{?1}{\mathbf{T}}_i^{?1}{\mathbf{T}}_j\right)}^{\vee }$$

緊接著就是經典的對$T_i$和$T_j$加左擾動對擾動求導
$${\hat{\mathbf{e}}}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{?1}{\mathbf{T}}_i^{?1}\exp \left({\left(?\mathbf{\delta }{\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right){\mathbf{T}}_j\right)}^{\vee }$$
因為上式擾動項被夾在中間，所以可以通過下面的伴隨性質：
$$\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{T}=\mathbf{T}\exp \left({\left(\mathrm{Ad}\left({\mathbf{T}}^{?1}\right)\mathbf{\xi }\right)}^{\wedge }\right)$$
將擾動挪到最右邊，最終得到下面的式子：

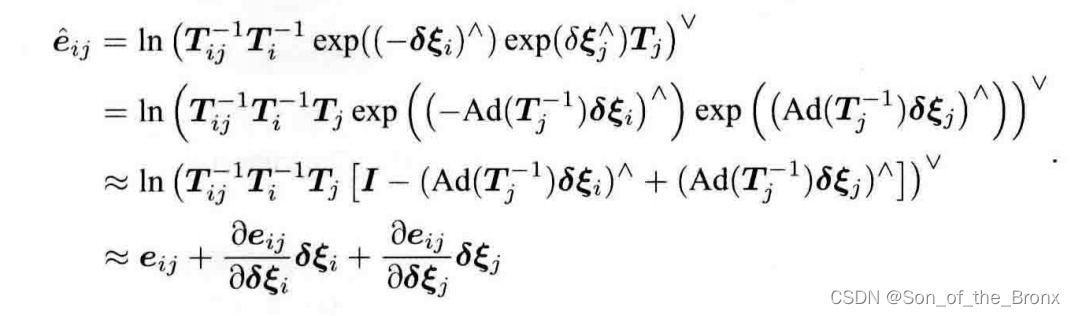
其實對于這個式子我不是很能理解從第三個式子到第四個式子的轉變，經過與其他人的交流，得知還需要借助ln(1+x)的泰勒展開結合se(3)的BCH近似來化簡，下面就是自己手寫的推導過程（從第三個式子開始推導）：

對于一開始的公式，我想的是直接從第二個式子展開，忽略了se(3)的BCH近似，結果雅可比跟書上那個是類似的，只不過書上多了一個可以忽略的$J_r$：

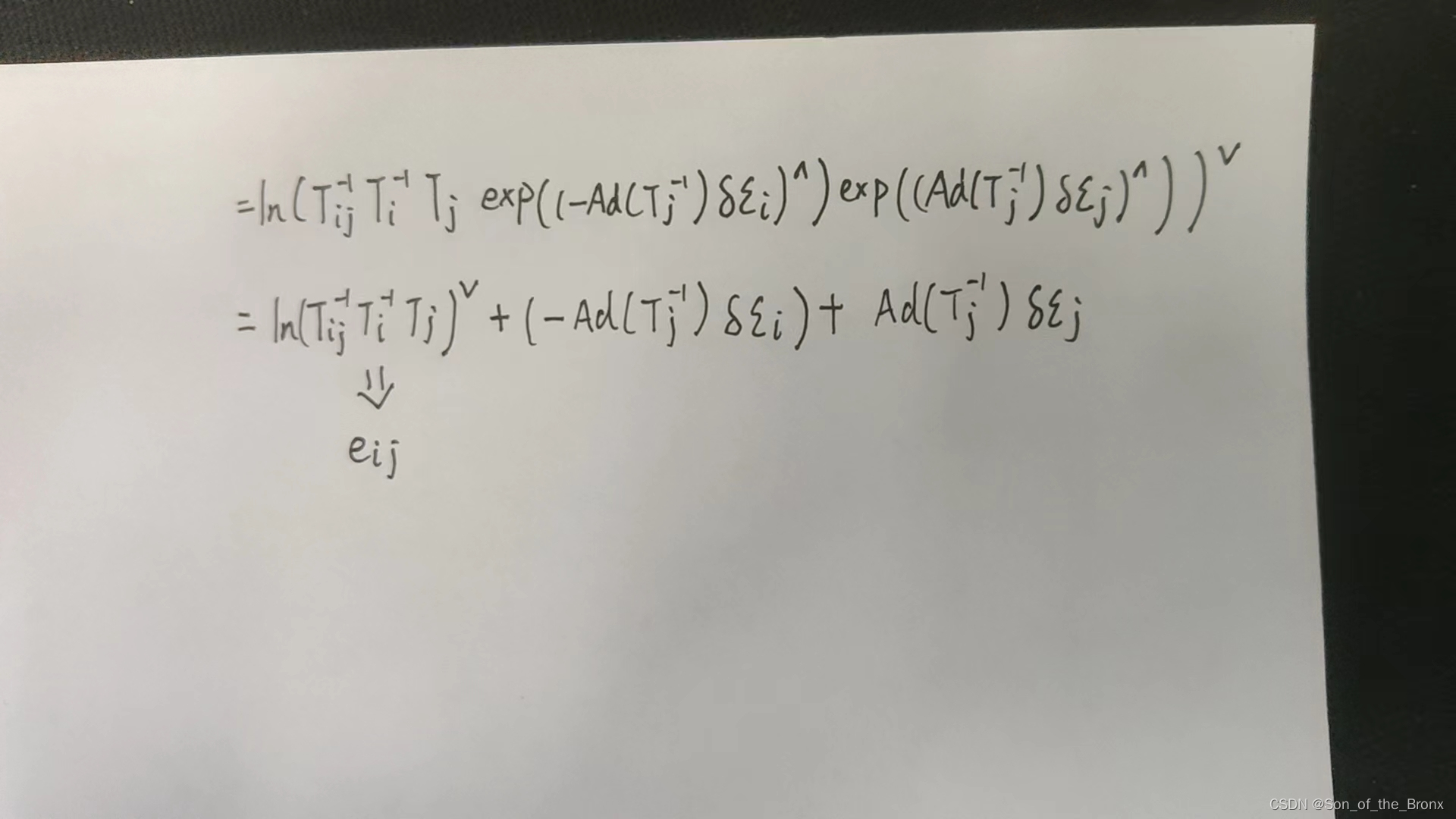
后續的過程就是根據雅可比去求增量方程，求解增量方程優化相機位姿，高斯牛頓的劇情又來了。

基于滑動窗口的后端

這里只考慮滑動窗口BA優化，因為書上對滑動窗口這部分介紹的東西比較少。

個人見解

為什么會想用滑動窗口的方式？就是因為在slam的過程中，圖像來了就算一幀，一幀需要優化一個相機位姿和幾百個特征點。時間一長，特征點數量就飛速增長，雖然可以采用關鍵幀的策略，但是關鍵幀的數量也是會隨著slam的過程逐漸增多。所以就產生控制BA規模的想法，最簡單的方法就是僅僅保存離當前幀時間最近的N個關鍵幀，依靠這些關鍵幀做BA優化。在新增關鍵幀和關鍵點的時候是比較好操作的，但是在刪除一個舊的關鍵幀時，就需要邊緣化的操作。

舊關鍵幀的邊緣化

具體其實可以參考一篇博客，寫的非常清晰：邊緣化中矩陣運算的一點細節

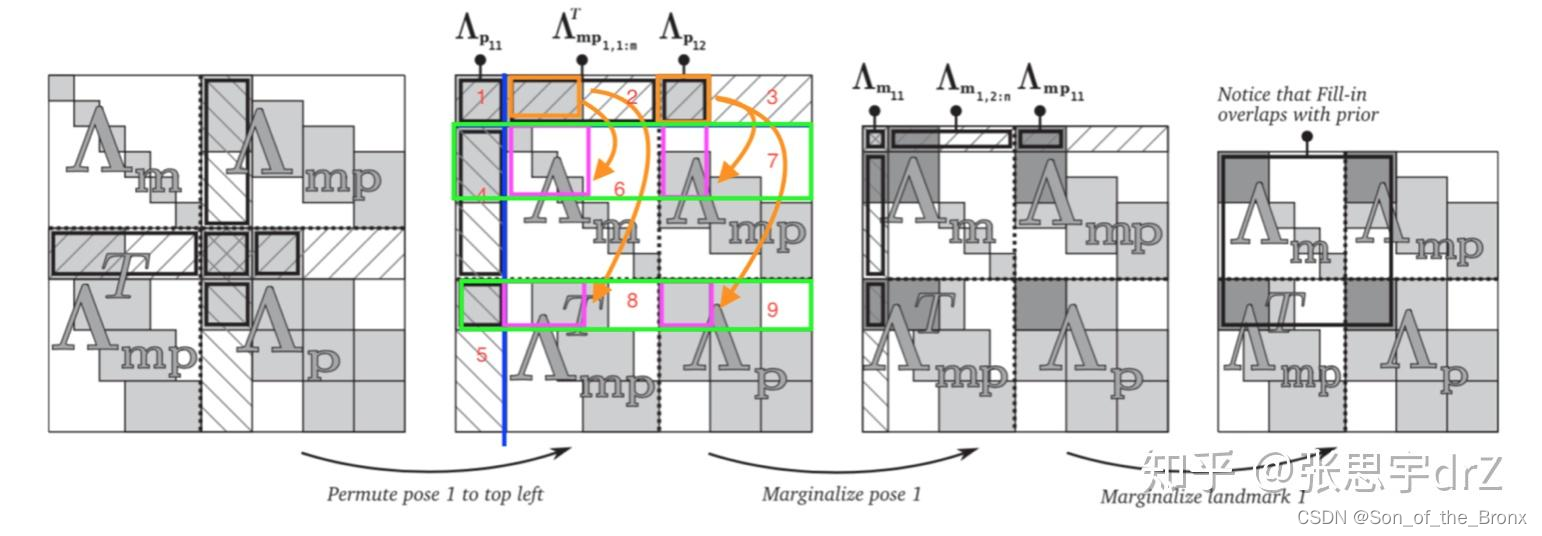
邊緣化的過程可以簡要的由上面的圖片來表示。這個就是整個滑動窗口的BA優化中H矩陣，$A_m$代表的是特征點的部分，$A_p$代表相機位姿的部分。先邊緣化相機位姿，這時候有關這個相機位姿的信息就會在schur消元的過程中 Fill-in $A_m$中，然后就是邊緣化這個相機位姿的特征點，也是通過schur消元中 Fill-in $A_m$中，但是Fill-in的范圍是一致的，不會有新的空白區域被 Fill-in ，最終就可以得到邊緣化后的H矩陣。

其實看到最后的H矩陣，$A_m$沒法保證自身是對角塊矩陣，所以在后續優化求解的時候，就無法通過之前稀疏方式去迭代求解了。這個問題應該也會有一些SLAM框架去解決，采取其他邊緣化策略保證$A_m$對角塊矩陣的特性。