數據結構：二叉樹與樹

一樹的基本概念：

1.樹的形狀：

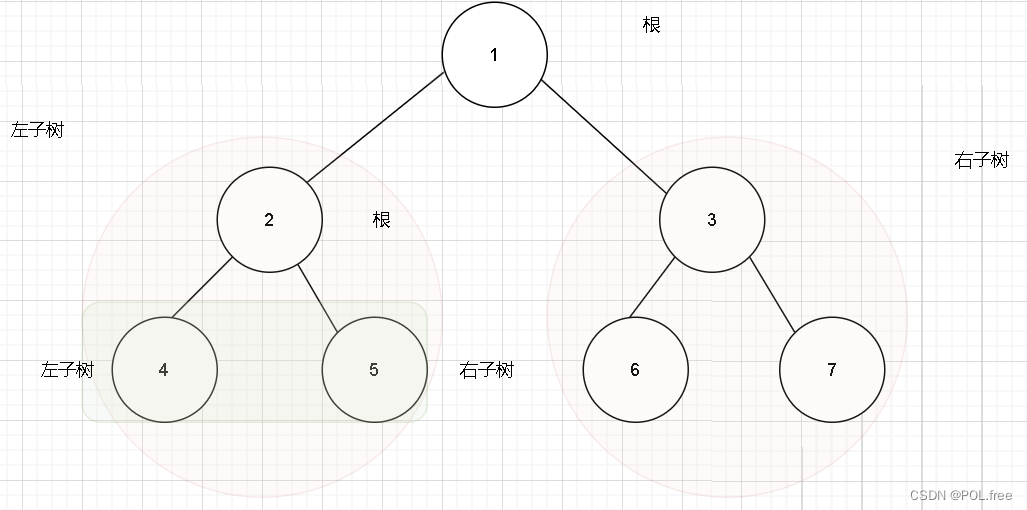
2.樹的定義：

樹是一種非線性的數據結構，它是n(n >= 0)個結點的有限集。當n = 0時，稱為空樹。在任意一棵非空樹中應滿足：

2.1 有且僅有一個特定的稱為根的結點。
2.2 當n > 1時，其余結點可分為m(m > 0)個互不相交的有限集T1 ……Tm，其中每個集合本身又是一棵樹，并且稱為根的子樹。
顯然，樹的定義是遞歸的，即在樹的定義中又用到其自身，樹是一種遞歸的數據結構。樹作為一種邏輯結構，同時也是一種分層結構，具有以下兩點特點：

2.3 樹的根結點沒有前驅，除根結點外的所有結點有且只有一個前驅。
2.4 樹中所有結點可以有零個或多個后繼。

3.樹中相關的關鍵詞概念：

3.1 節點的度：一個節點含有的子樹的個數稱為該節點的度；如上圖：A的為6

3.2 路徑：樹的路徑是指從根節點到樹內特定節點遍歷的節點序列

3.3 根：樹頂端的節點稱為根。一棵樹只有一個根，如果要把一個節點和邊的集合稱為樹，那么從根到其他任何一個節點都必須有且只有一條路徑。A是根節點

3.4 父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點；如上圖：A是B的父節點

3.5 子節點：一個節點含有的子樹的根節點稱為該節點的子節點；如上圖：B是A的子節點

3.6 兄弟節點：具有相同父節點的節點互稱為兄弟節點如上圖：I與J就是兄弟

3.7 堂兄弟節點：不是相同父親的節點且在同一層而和相鄰的稱堂兄弟節點如上圖：H與I就是堂兄弟

3.8 葉節點：度為0的節點就是葉節點或者說沒有孩子的節點?如上圖：P和Q

3.9 分支節點：度不為0的點。列如：B、C、D、都是分支節點。

3.10 子樹：每個節點都可以作為子樹的根，它和它所有的子節點、子節點的子節點等都包含在子樹中。

3.11 節點的層次：從根開始定義，根為第一層，根的子節點為第二層，以此類推。

3.12 深度 \ 高度：樹中節點的最大層。如圖就是4。

3.13 節點的祖先：從根到該節點的所經過分支上的所有節點，A就是所有節點的祖先。

3.14 深林：互不相交的樹的集合被稱為深林。

3.15 子孫：以某節點為根的子樹的子樹中任一節點都被稱為該節點的子孫。列如所有節點都是A的子孫

4.樹的性質：

4.1 樹中的結點數等于所有結點的度數之和加1
4.2 度為m的樹中第i層上至多有m^(i-1)個結點(i >= 1)
4.3 高度為h的m叉樹至多有(m^h - 1)/(m - 1)個結點
4.4 具有n個結點的m二叉的最小高度為[logm(n(m - 1) + 1)]

二二叉樹的基本概念：

1.二叉樹的形狀：

2.二叉樹的定義：

二叉樹是另一種樹形結構，其特點時每個結點至多只能有兩棵樹(即二叉樹中不存在度大于2的結點)，并且二叉樹的子樹也有左右之分，其次序不能任意顛倒。

與樹相似，二叉樹也有遞歸的形式定義。二叉樹是n(n >= 0)個結點的有限集合：

2.1 或者為空二叉樹，即n = 0.
2.2 或者由一個根結點和兩個互不相交的被稱為根的左子樹和右子樹組合。左子樹和右子樹又是分別? 是一棵二叉樹
二叉樹是有序樹，若將其左右子樹顛倒，則成為另一顆不同的二叉樹。即使樹中結點只有一顆子樹，也要區分它是左子樹還是右子樹。

3.二叉樹的性質：

3.1 非空二叉樹上的葉子節點數等于度為2的結點數加1，n0 = n1 + 1
3.2 非空二叉樹上第k層上至多有2^(k-1)個結點(k >= 1)
3.3 高度為h二叉樹至多有2^(h - 1)個結點(h >= 1)
3.4 對完全二叉樹按從上到下、左到右的順序依次編號1，2……n
3.5 具有n個(n > 0)結點的完全二叉樹的高度為[log2(n + 1)]或[log2n] + 1

三特殊的二叉樹：

1.滿二叉樹(FBT)：

1.1 所有非葉節點都擁有兩個子節點。

1.2 最深層的葉子節點從左到右依次排列，沒有空缺。

1.3 深度為 h 的完全二叉樹，具有 2^h - 1 個節點。

2.完全二叉樹(CBT)：

2.1 每一層都擁有最大數量的節點。

2.2 深度為 k 的滿二叉樹，具有 2^k - 1 個節點。

2.3 非葉節點都擁有兩個子節點，最底層可能存在一些空缺。

3.滿二叉樹和完全二叉樹的形狀：

四二叉樹的存儲結構：

1.順序存儲結構：

二叉樹的順序存儲是指使用一維數組來存儲二叉樹中的節點，并將節點的邏輯結構映射到數組的物理結構中。這種存儲方式通常用于空間受限的場景，因為只需要一個數組即可存儲整個二叉樹。

?2.為什么二叉樹的順序存儲只能應用于完全二叉樹？

2.1 節點索引與子節點關系： 在順序存儲中，節點的索引與它的子節點之間存在著固定的關系。例如，對于一個節點 i，它的左子節點的索引為 2i，右子節點的索引為 2i + 1。這種關系依賴于完全二叉樹的結構特點，即每個非葉節點都擁有兩個子節點。

2.2 空間利用率： 順序存儲旨在節省空間，因此需要盡可能地利用數組空間。在完全二叉樹中，所有非葉節點都擁有兩個子節點，因此數組空間可以得到充分利用。而對于非完全二叉樹，可能存在一些節點只有一個子節點或沒有子節點，導致數組空間浪費。

2.3 空缺節點處理： 在非完全二叉樹中，可能存在空缺節點，即沒有實際內容的節點。順序存儲難以有效地處理這些空缺節點，因為它們會破壞節點索引與子節點關系的約定。

2.4 算法復雜度： 對于非完全二叉樹，順序存儲需要額外的機制來處理空缺節點，這會導致算法復雜度的增加，降低效率。

3.完全二叉樹的順序存儲與非完全二叉樹存儲形狀的區別：

2.堆(Heap)：

堆的定義：

堆（Heap）是一種特殊的樹形數據結構，它滿足堆性質：允許高效地檢索和刪除最大/最小元素。堆通常用于實現優先隊列。

堆的性質：

在堆中，每個非葉節點的值都應該大于或等于其子節點的值（最大堆）或者小于或等于其子節點的值（最小堆）。

堆通常使用完全二叉樹來實現，因為完全二叉樹結構可以保證堆性質的有效性和空間利用率。

在最大堆中，根節點是堆中最大的元素；在最小堆中，根節點是堆中最小的元素。

堆的種類:

根據堆性質的不同，堆可以分為兩種類型：

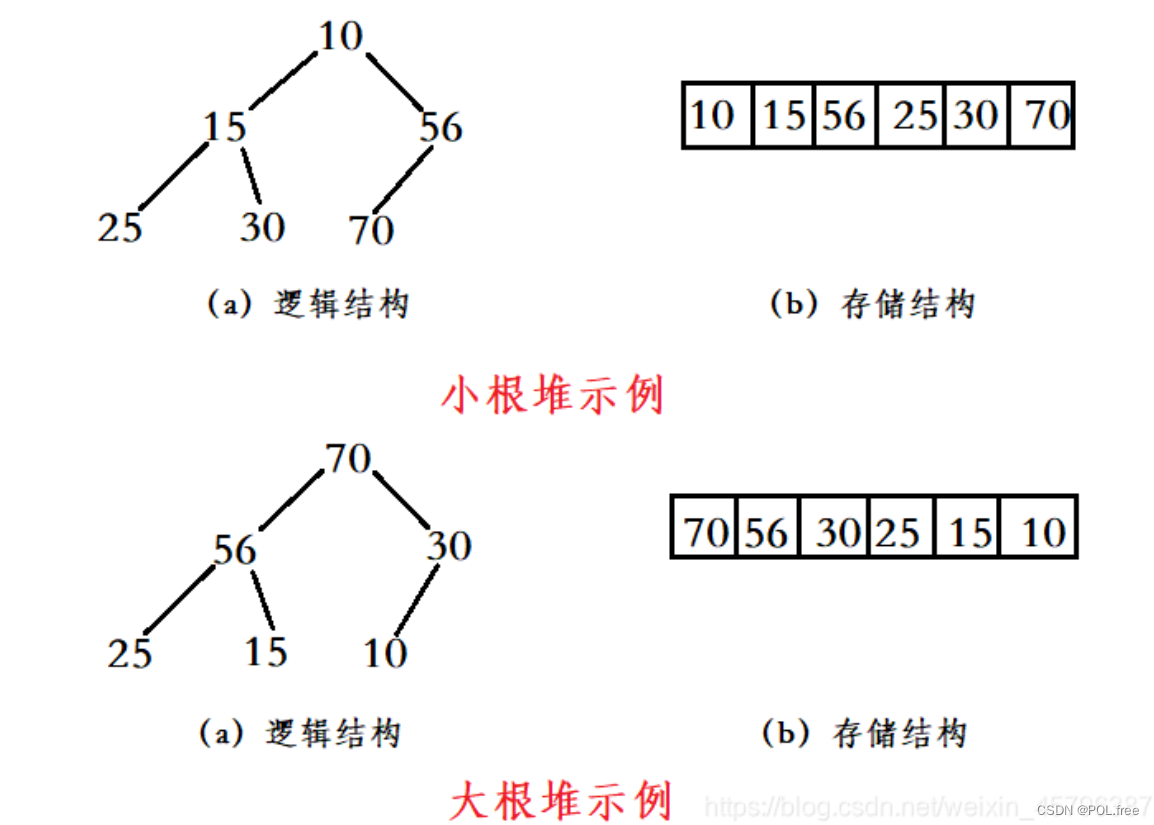
最大堆： 在最大堆中，每個非葉節點的值都大于或等于其子節點的值。根節點是堆中最大的元素。

最小堆： 在最小堆中，每個非葉節點的值都小于或等于其子節點的值。根節點是堆中最小的元素。

最大堆與最小堆的形狀：

3.順序存儲代碼實現：

堆的存儲結構：

typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

堆的所有接口：

//初始化、銷毀
void HPInit(HP* php);
void HPDestroy(HP* php);// 插入
void HPPush(HP* php, HPDataType x);//獲取堆頂元素、堆的有效數據個數
HPDataType HPTop(HP* php);
HPDataType HPsize(HP* php);// 刪除堆頂的數據
void HPPop(HP* php);//判斷堆是否為空
bool HPEmpty(HP* php);

堆的初始化：

void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}

輸出：

堆的銷毀：

void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}

輸出：

插入：

void HPPush(HP* php, HPDataType x)
{assert(php);//擴容數組if (php->capacity == php->size){HPDataType Newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* Ptmp = (HPDataType*)realloc(php->a , sizeof(HPDataType) * Newcapacity);if (Ptmp == NULL){perror("calloc error");exit(-1);}php->a = Ptmp;php->capacity = Newcapacity;	}php->a[php->size] = x;php->size++;//向上調整AdjustUp(php->a, php->size - 1); //因為php->size最后是指向最后數據的后面一個所以傳要減一
}

輸出：

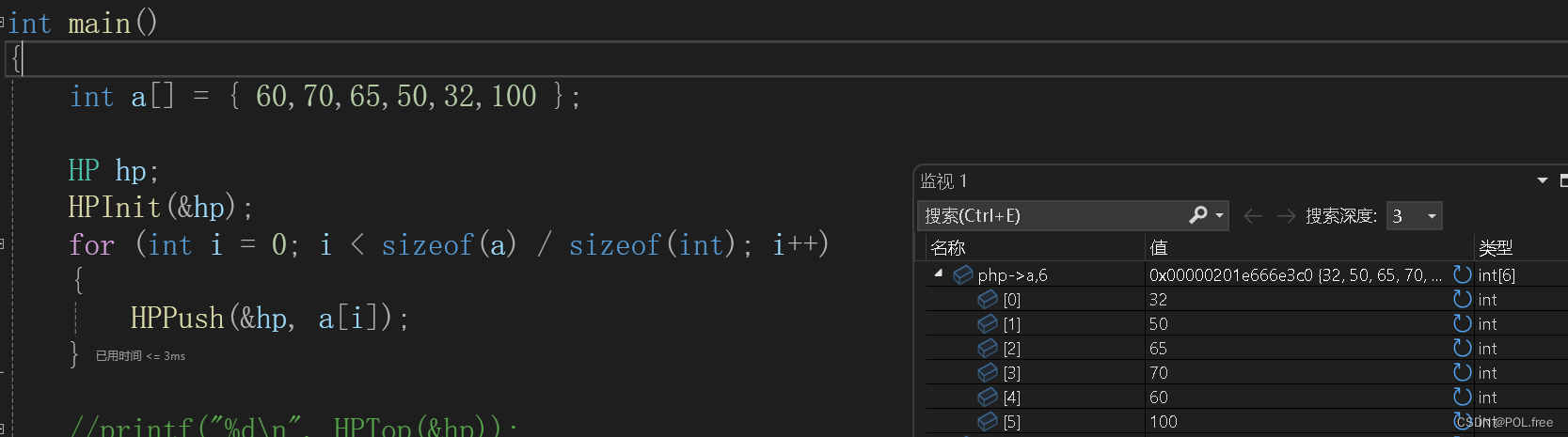
向上調整(建小堆)：

void AdjustUp(HPDataType* a , HPDataType child)
{HPDataType parents = (child - 1) / 2;//找父節點while (child > 0)//當child走到首節點時就會停止循環{if (a[child] < a[parents]){Swap(&a[child] , &a[parents]);//交換數據child = parents;parents = (parents - 1) / 2;//改變父親指針的指向，讓父親指針往上指}else{break;}}
}

交換父子數據：

void Swap(HPDataType* x , HPDataType* y)
{int tmp = *x;*x = *y;*y = tmp;
}

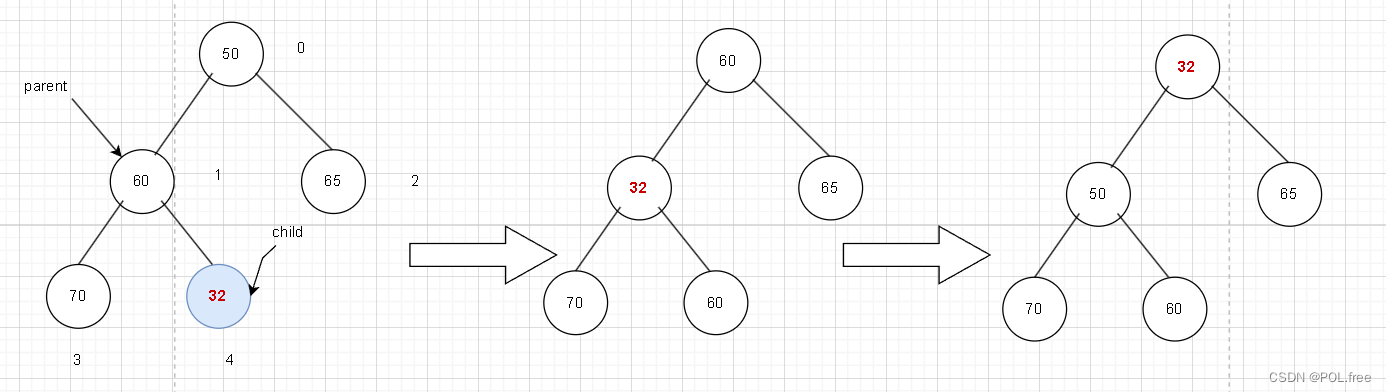
當堆(小堆)要插入新數據時在邏輯層面上是在堆的最右下方插入一個值而在物理層面上是直接在添加在數組的后面，而我們插入一個值必然會改變小堆(大堆)的性質所以需要向上調整以此來保持，所以當插入32時首先需要找到父親節點然后再跟它比下大小如果新插入的節點比它小那就需要調整，把數據互相交換然后讓孩子指向父親然后再讓父親指向父親同時要查看數據的大小，當child小于0時就可以退出了

獲取堆頂(最大或最小)的元素：

HPDataType HPTop(HP* php)
{assert(php);return php->a[0];
}

輸出：

獲取堆的數據個數：

HPDataType HPsize(HP* php)
{assert(php);return php->size;
}

輸出：

刪除堆頂的數據：

void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0] , &php->a[php->size-1]);//先首尾交換php->size--;//刪除尾部數據(實際上是隱藏交換之后的尾部數據)AdjustDown(php->a , php->size ,0);//向下調整
}

輸出：

雖然50 32還是顯示但是我們靠自減已經將他們在邏輯層面給刪除了但是再物理層面上還是帶顯示的

向下調整(逐個刪除每個數據)：

void AdjustDown(HPDataType* a , HPDataType n , HPDataType parents)
{HPDataType child = (parents * 2) + 1;while (child < n){//假設child指向左孩子if (child + 1 < n && a[child] > a[child + 1])//選出左右孩子誰大誰小{child++;//如果右孩子小那就讓child指針自增指向右孩指就行}if (a[child] < a[parents]){Swap(&a[child], &a[parents]);child = parents;child = (parents * 2) + 1;}else{break;}}}

判斷堆是否為空：

bool HPEmpty(HP* php)
{assert(php);if (php->size == 0){return false;}return true;//return php->size == 0;
}

輸出：

打印堆：

4.鏈表存儲結構：

鏈式二叉樹是一種非線性數據結構，它使用鏈接而不是連續的內存布局來表示元素之間的層次關系。與將節點存儲在數組中的傳統二叉樹不同，鏈式二叉樹使用指針來連接節點，從而為節點分配和動態內存管理提供了靈活性。

二叉樹的前序，中序，后序遍歷:

二叉樹遍歷是指對二叉樹中的每個節點恰好訪問一次的系統過程。它是探索和操作二叉樹的基本技術。三種常見的遍歷方法是前序、中序、后序。

前序遍歷：

在前序遍歷中，首先訪問根結點，然后訪問左子樹，最后訪問右子樹?如上圖：

遍歷順序：

首先訪問根節點 1 ，然后再訪問根節點 1 的左子樹 2 最后再訪問以 2 為根節點的左子樹 4，接下來就是訪問以 4 為根節點的左子樹 NULL 與右子樹 NULL?

1 2 4 NULL NULL

當右子樹是NULL那就需要向上返回，先是返回到 4 但因 4 已經遍歷過了所以需要再次向上返回，返回到 2 但因 2 已經遍歷過了但以它為根節點的右子樹并沒有被遍歷過所以就先訪問以 2 為根節點的右子樹 5 ，最后訪問以5為根的左子樹 NULL 和右子樹 NULL

5 NULL NULL

這里需要直接返回到 1 這里就不過多解釋了思想和上面一樣，遍歷以 1 為根節點的右子樹 3 然后再遍歷以 3 為根節點的左子樹 6 然后再訪問以 3 為根節點的左子樹 NULL 和右子樹 NULL，接下來需要返回到以 3 為根節點的右子樹 7最后訪問以 7 為根節點的左子樹 NULL 和右子樹 NULL

3 6 NULL NULL 7 NULL NULL

它的完整順序就是 1 2 4 NULL NULL? 5 NULL NULL 3 6 NULL NULL 7 NULL NULL

中序遍歷：

在中序遍歷中，首先訪問左子樹，然后訪問根結點，最后訪問右子樹?如上圖：

遍歷順序：

首先是訪問根節點的左子樹 2 然后再訪問以 2 為根節點的左子樹 4最后再訪問以 4 為根節點的左子樹 NULL當碰到NULL就可以返回到根節點 4 最后再訪問以 4 為根節點的右子樹 NULL

?NULL 4 NULL

訪問完以 4 為根節點的左樹右樹那就需要繼續向上返回到根節點 2 因只遍歷過以根節點的 2 的左子樹但右子樹并沒有遍歷所以現在需要遍歷右子樹，先遍歷以根節點 5 的左子樹 NULL然后再遍歷根節點 5 最后需遍歷以根節點 5 的右子樹 NULL

2 NULL 5 NULL

當以根節點 1 的左子樹全部遍歷完所以就需要遍歷根節點 1 了? 那么遍歷完左子樹根節點那就需要遍歷右子樹了。先訪問以根節點 1 的右子樹 3然后再訪問以根節點 3 的左子樹 6 然后再遍歷以根節點 6 的左子樹 NULL當碰到 NULL 那這個程序就需要返回到根節點 6 然后向右訪問 NULL碰到NULL那就需要再次返回到根節點 3 ，以3的左子樹已經全部訪問完所以就需要向右訪問以此循環

1?NULL 6 NULL 3?NULL?7 NULL

它的完整順序就是 NULL 4 NULL 2 NULL 5 NULL 1?NULL 6 NULL 3?NULL?7 NULL

后序遍歷：

在后序遍歷中，首先訪問左子樹，然后訪問右子樹，最后訪問根結點?如上圖：

遍歷順序：

首先是訪問根節點的左子樹 2 然后再訪問以 2 為根節點的左子樹 4最后再訪問以 4 為根節點的左子樹 NULL當碰到NULL就可以返回到根節點 4 但是根節點是最后才訪問的所以現在不能訪問 4 而是先訪問以 4 為根節點的右子樹 NULL最后再訪問以 4 為根節點

NULL NULL 4

訪問完根節點 4 之后就需要向上返回到以 2?為根節點但是后序的訪問順序是先訪問左右最后再訪問根節點的所以我們需要向以 2 為根節點的右遍歷左子樹與右子樹 NULL最后再訪問根節點 5。

NULL NULL 5

訪問完以 2 為根節點的左子樹與右子樹那么就可以訪問根節點了但是根節點 2 也是也是以 1 為根節點的左子樹，現在以 1 為左子樹已經訪問完那就可以訪問以 1 為根節點的右子樹了所以我們現在向右遍歷直到遍歷到以 6 為根節點的左子樹 NULL 然后就需開始返回到根節點 6 然后再向右子樹 NULL 最后再訪問根節點 6

NULL NULL 6

訪問根節點 6 之后就和以根節點 1 為左子樹的 2 一樣這里我就不重新贅述了最后訪問完以 1 為右子樹就需要訪問根節點 1 了

NULL NULL 7 3 1

它的完整順序就是 NULL NULL 4 NULL NULL 5 2 NULL NULL 6 NULL NULL 7 3 1

4.鏈式存儲代碼實現：

鏈式存儲結構：

typedef int BTDataType;
typedef struct BinaryTree
{struct BinaryTree* left;//左子樹struct BinaryTree* right;//右子樹BTDataType data;
}BT;

鏈式存儲所有接口：

//二叉樹的初始化
BT* CreatTreeNode(int x);//二叉樹的銷毀
void DestroyBinaryTree(BT* root);//前序遍歷、中序遍歷、后序遍歷
void PrevOrder(BT* root);
void InOrder(BT* root);
void PostOrder(BT* root);//獲取二叉樹相關個數
int BinaryTreeSize(BT* root);//獲取葉子節點相關個數
int BinaryTreeleafSize(BT* root);//獲取樹的高度
int  BinaryTreeHeight(BT* root);//計算第K層節點個數
int  BinaryTreeKcount(BT* root, BTDataType k);

鏈式存儲初始化：

BT* CreatTreeNode(int x)
{BT* Newnode = (BT*)malloc(sizeof(BT));if (Newnode == NULL){perror("malloc error");return NULL;}Newnode->data = x;Newnode->left = NULL;Newnode->right = NULL;return Newnode;
}

輸出：

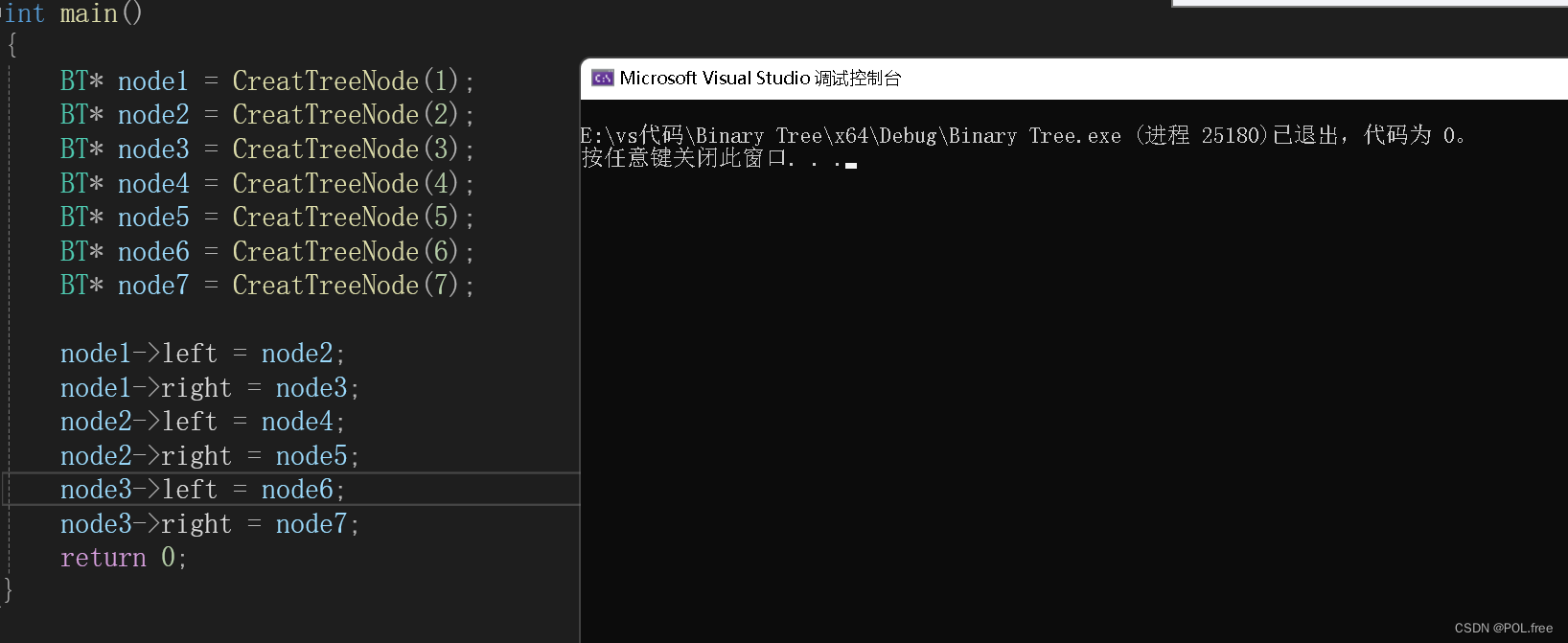
鏈式存儲銷毀：

void DestroyBinaryTree(BT* root)
{if (root == NULL){return;}DestroyBinaryTree(root->left);DestroyBinaryTree(root->right);free(root);
}

輸出：

前序遍歷：

void PrevOrder(BT* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

輸出：

中續遍歷：

void InOrder(BT* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

輸出：

后續遍歷：

void PostOrder(BT* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

輸出：

獲取二叉樹相關個數：

int BinaryTreeSize(BT* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

輸出：

獲取葉子節點相關個數：

int BinaryTreeleafSize(BT* root)
{if (root->left == NULL && root->right == NULL){return 1;}if (root == NULL){return 0;}else{return BinaryTreeleafSize(root->left) + BinaryTreeleafSize(root->right);}
}

輸出：

獲取樹的高度：

int  BinaryTreeHeight(BT* root)
{if (root == NULL){return 0;}BTDataType Tleft = BinaryTreeHeight(root->left);BTDataType Tright = BinaryTreeHeight(root->right);return Tleft > Tright ? Tleft + 1 : Tright + 1;}

輸出：

計算第K層節點個數：

int  BinaryTreeKcount(BT* root, BTDataType k)
{if (root == NULL || k < 1){return 0;}if (k == 1){return 1;}return BinaryTreeKcount(root->left, k - 1) + BinaryTreeKcount(root->right, k - 1);
}

輸出：