z3-加法器實驗

補碼器加減法，運算方法簡介

我們要知道什么是補碼的加法，我們為什么要用補碼的加法？

補碼的加法其實就是將兩個補碼形式的二進制數字直接相加，處理的時候忽略超出固定位數的進位。補碼的加法運算和無符號二進制數的加法操作一樣，不需要額外處理負號或減法的邏輯

補碼加法的具體操作步驟：

  1. 將兩個補碼數位對齊（確保位數一致）
  2. 諸位相加，處理進位
  3. 如果結果超出固定的位數，忽略超出部分的進位

例子：
假如我們在一個8位的系統中進行加法計算

  • 5+3
    • 5的補碼：00000101
    • 3的補碼：00000011
    • 00001000（結果位8）
  • 5+(-3)
    • 5的補碼：00000101
    • -3的補碼：11111101
    • 相加：10000010（結果位-2，最高位1表示結果是負數）

那么我們為什么要使用補碼的加法？

補碼的使用簡化了計算機硬件的設計，使有符號的整數運算變得更加高效統一。補碼的使用還簡化了負數的表示和處理，使計算機更方便地進行各種數值運算。

在了解了補碼的加法之后我們就可以嘗試設計一位全加器電路了

構造一個一位全加器

首先要知道什么是全加器？

全加器是一種基本的數字電路，用于二進制數的加法運算。它能夠同時處理兩個二進制數的加法運算。它能夠同時處理兩個二進制位和一個來自低位的進位輸入，并輸出該位的和以及進位到高位的值。全加器是構建多位二進制加法器的基本模塊。

全加器的功能

全加器有三個輸入兩個輸出：

  • 輸入：兩個被加的二進制位A和B，以及來自前一位的進位輸入C_in_
  • 輸出：該位的和S和向更高位傳遞的進位輸出C_out_

全加器的真值表

ABC_in_SC_out_
00000
00110
01010
01101
10010
10101
11001
11111

全加器的邏輯表達式

根據真值表，全加器的輸入S和輸出C可以用邏輯表達式表示：

  • 和（sum）S：S = A XOR B XOR C_in_
  • 進位（Carry）C_out_：C_out_ = (A * B) + (B * C_in_) + (A * C_in_)

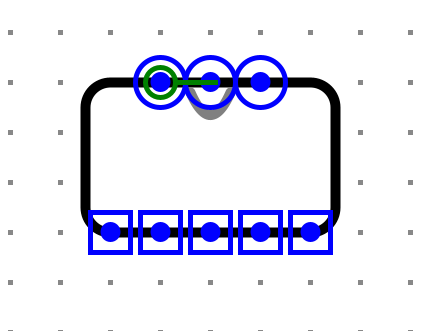
一位全加器的電路實現

如下圖所示：
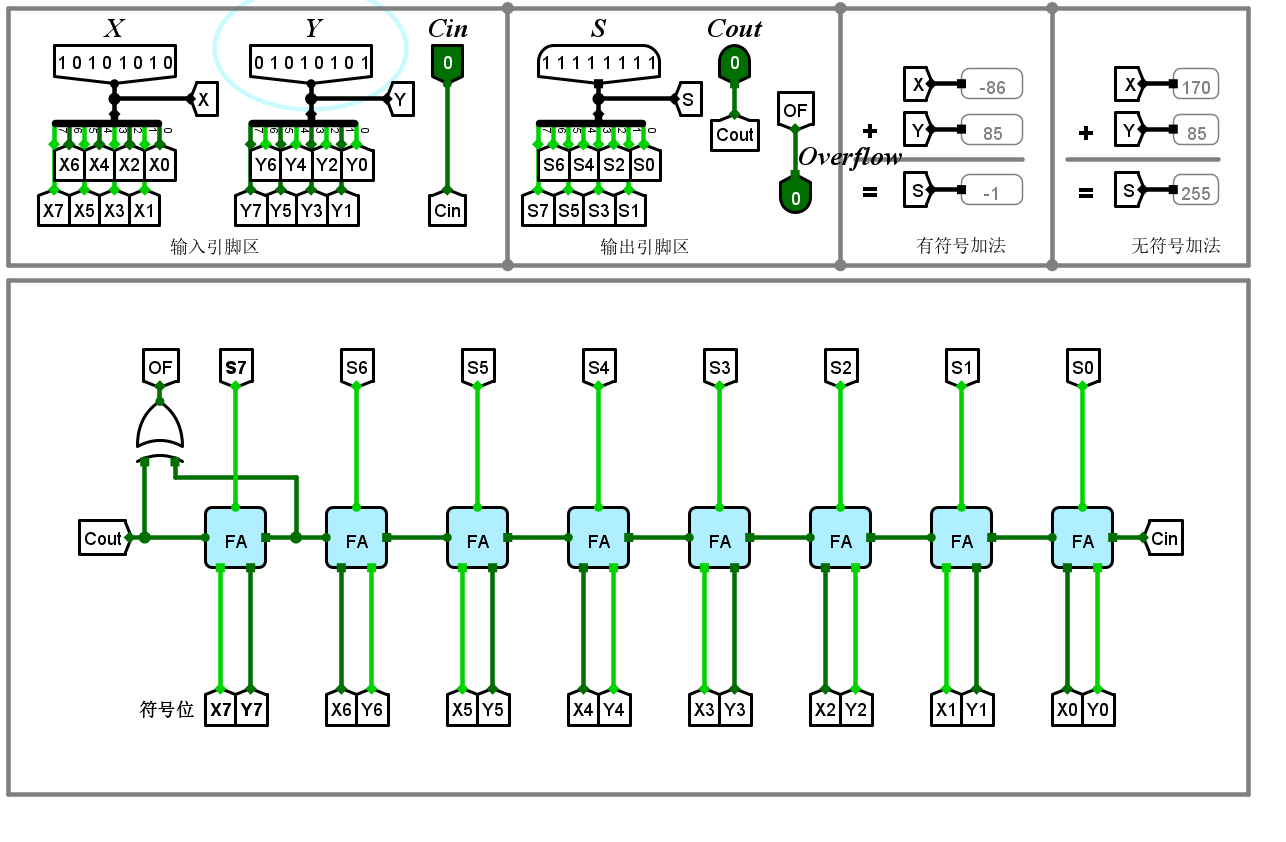
image.png
功能封裝
image.png

八位串行加法器

八位串行加法器是一種可以對兩個8位二進制數進行加法運算的電路，串行加法器的工作原理是每次處理一個位，并將進位傳遞到下一位進行累加。以下是八位串行加法器的詳細電路設計和驗證。

電路設計

  • 全加器：用于對兩個二進制位及一個進位進行相加。
  • 移位寄存器：用于存儲和移位操作，分別存儲兩個8位數加數和結果
  • **D觸發器：**用于存儲和傳遞進位
  • 時鐘：用于同步操作

電路示意圖

image.png

使用具體數字驗證

1. 初始化
  • A寄存器：10101010
  • B寄存器：01010101
  • 進位 𝐶0：0
2. 逐位相加
  1. 第1次時鐘脈沖：
    • 取出最低位：A0 = 0, B0 = 1, 𝐶0=0
    • 全加器計算：𝑆0=0⊕1⊕0=1
    • 進位：𝐶1=(0?1)+(1?0)+(0?0)=0
    • 移位：A -> 01010101, B -> 00101010
  2. 第2次時鐘脈沖：
    • 取出當前位：A1 = 1, B1 = 0, 𝐶1=0
    • 全加器計算：𝑆1=1⊕0⊕0=1
    • 進位：𝐶2=(1?0)+(0?0)+(1?0)=0
    • 移位：A -> 00101010, B -> 00010101
  3. 第3次時鐘脈沖：
    • 取出當前位：A2 = 0, B2 = 1, 𝐶2=0
    • 全加器計算：𝑆2=0⊕1⊕0=1
    • 進位：𝐶3=(0?1)+(1?0)+(0?0)=0
    • 移位：A -> 00010101, B -> 00001010
  4. 第4次時鐘脈沖：
    • 取出當前位：A3 = 1, B3 = 0, 𝐶3=0
    • 全加器計算：𝑆3=1⊕0⊕0=1
    • 進位：𝐶4=(1?0)+(0?0)+(1?0)=0
    • 移位：A -> 00001010, B -> 00000101
  5. 第5次時鐘脈沖：
    • 取出當前位：A4 = 0, B4 = 1, 𝐶4=0
    • 全加器計算：𝑆4=0⊕1⊕0=1
    • 進位：𝐶5=(0?1)+(1?0)+(0?0)=0
    • 移位：A -> 00000101, B -> 00000010
  6. 第6次時鐘脈沖：
    • 取出當前位：A5 = 1, B5 = 0, 𝐶5=0
    • 全加器計算：𝑆5=1⊕0⊕0=1
    • 進位：𝐶6=(1?0)+(0?0)+(1?0)=0
    • 移位：A -> 00000010, B -> 00000001
  7. 第7次時鐘脈沖：
    • 取出當前位：A6 = 0, B6 = 1, 𝐶6=0
    • 全加器計算：𝑆6=0⊕1⊕0=1
    • 進位：𝐶7=(0?1)+(1?0)+(0?0)=0
    • 移位：A -> 00000001, B -> 00000000
  8. 第8次時鐘脈沖：
    • 取出當前位：A7 = 1, B7 = 0, 𝐶7=0
    • 全加器計算：𝑆7=1⊕0⊕0=1
    • 進位：𝐶8=(1?0)+(0?0)+(1?0)=0

結果

最終輸出結果的各位和為 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=11111111，即十進制的255。進位輸出 𝐶8=0，表示沒有產生進位。
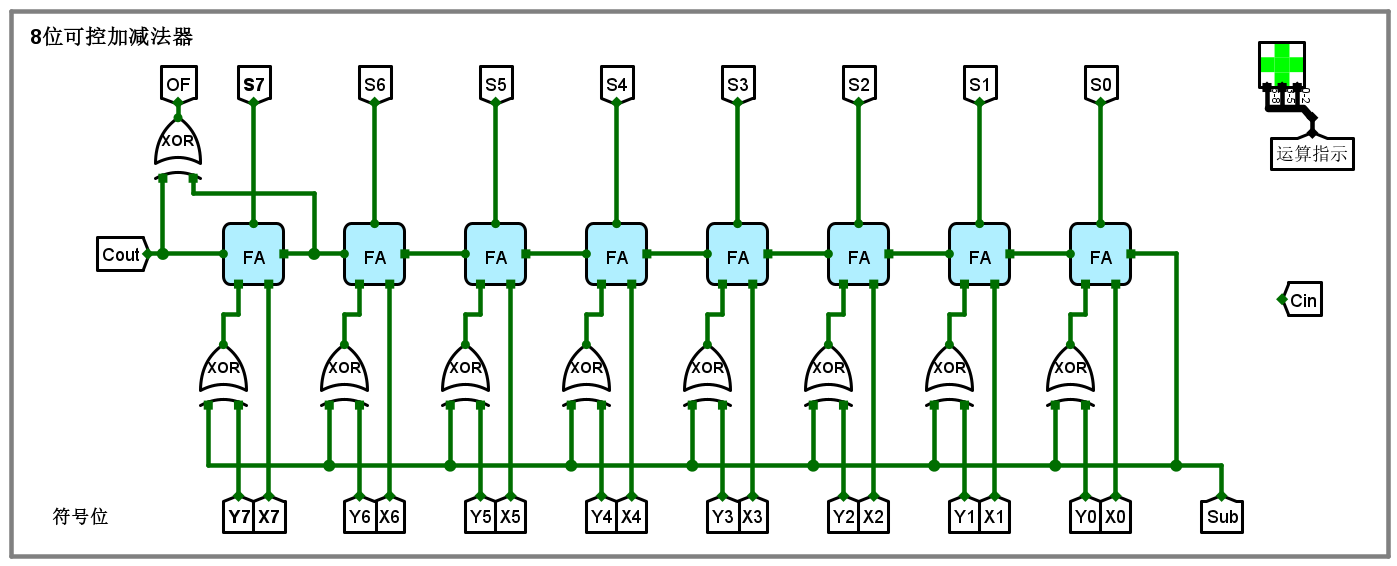
image.png

八位可控加減法器

8位可控加減法器是一種能夠對兩個8位二進制數進行加法或減法運算的電路。它通過控制信號來決定是執行加法還是減法。減法可以通過將被減數取補碼并進行加法來實現。以下是詳細的電路設計和使用具體數字進行驗證的步驟。

電路設計

  • 全加器：用于對兩個二進制位及一個進位進行相加。
  • 移位寄存器：用于存儲和移位操作，分別存儲兩個八位數和結果。
  • D觸發器：用于存儲和傳遞進位。
  • 時鐘：用于同步操作。
  • 異或門：用于將減法操作轉化為加法操作。
  • 控制信號：用于選擇加法或減法操作。

電路示意圖

image.png

使用具體數字驗證

加法驗證

假設我們要相加的兩個8位數是：

  • A = 01101101 (十進制的109)
  • B = 00111011 (十進制的59)
  1. 初始化：
    • A寄存器：01101101
    • B寄存器：00111011
    • 進位 _C_0：0
    • 控制信號 Add/Sub = 0（加法）
  2. 逐位相加
  • 第1次時鐘脈沖：
    • 取出最低位：A0 = 1, B0 = 1, 𝐶0=0
    • 全加器計算：𝑆0=1⊕1⊕0=0
    • 進位：𝐶1=(1?1)+(1?0)+(0?0)=1
    • 移位：A -> 00110110, B -> 00011101
  • 第2次時鐘脈沖：
    • 取出當前位：A1 = 0, B1 = 1, 𝐶1=1
    • 全加器計算：𝑆1=0⊕1⊕1=0
    • 進位：𝐶2=(0?1)+(1?1)+(0?1)=1
    • 移位：A -> 00011011, B -> 00001110
  • 第3次時鐘脈沖：
    • 取出當前位：A2 = 1, B2 = 1, 𝐶2=1
    • 全加器計算：𝑆2=1⊕1⊕1=1
    • 進位：𝐶3=(1?1)+(1?1)+(1?1)=1
    • 移位：A -> 00001101, B -> 00000111
  • 第4次時鐘脈沖：
    • 取出當前位：A3 = 1, B3 = 0, 𝐶3=1
    • 全加器計算：𝑆3=1⊕0⊕1=0
    • 進位：𝐶4=(1?0)+(0?1)+(1?1)=1
    • 移位：A -> 00000110, B -> 00000011
  • 第5次時鐘脈沖：
    • 取出當前位：A4 = 0, B4 = 1, 𝐶4=1
    • 全加器計算：𝑆4=0⊕1⊕1=0
    • 進位：𝐶5=(0?1)+(1?1)+(0?1)=1
    • 移位：A -> 00000011, B -> 00000001
  • 第6次時鐘脈沖：
    • 取出當前位：A5 = 1, B5 = 1, 𝐶5=1
    • 全加器計算：𝑆5=1⊕1⊕1=1
    • 進位：𝐶6=(1?1)+(1?1)+(1?1)=1
    • 移位：A -> 00000001, B -> 00000000
  • 第7次時鐘脈沖：
    • 取出當前位：A6 = 0, B6 = 0, 𝐶6=1
    • 全加器計算：𝑆6=0⊕0⊕1=1
    • 進位：𝐶7=(0?0)+(0?1)+(0?1)=0
    • 移位：A -> 00000000, B -> 00000000
  • 第8次時鐘脈沖：
    • 取出當前位：A7 = 0, B7 = 0, 𝐶7=0
    • 全加器計算：𝑆7=0⊕0⊕0=0
    • 進位：𝐶8=(0?0)+(0?0)+(0?0)=0
結果

最終輸出結果的各位和為 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=10101000，即十進制的168。
image.png

減法驗證

初始化
  • A寄存器：01101101
  • B寄存器：00111011
  • 進位 _C_0：1（由于使用補碼減法，初始進位為1）
  • 控制信號 Add/Sub = 1（減法）
逐位計算（將B取反再加上A）
  1. 第1次時鐘脈沖：
    • 取出最低位：A0 = 1, B0 = 1
    • 由于控制信號為1，B0取反：B0’ = 0
    • 全加器計算：𝑆0=1⊕0⊕1=0
    • 進位：𝐶1=(1?0)+(0?1)+(1?1)=1
    • 移位：A -> 00110110, B -> 00011101
  2. 第2次時鐘脈沖：
    • 取出當前位：A1 = 0, B1 = 1
    • 由于控制信號為1，B1取反：B1’ = 0
    • 全加器計算：𝑆1=0⊕0⊕1=1
    • 進位：𝐶2=(0?0)+(0?1)+(0?1)=0
    • 移位：A -> 00011011, B -> 00001110
  3. 第3次時鐘脈沖：
    • 取出當前位：A2 = 1, B2 = 1
    • 由于控制信號為1，B2取反：B2’ = 0
    • 全加器計算：𝑆2=1⊕0⊕0=1
    • 進位：𝐶3=(1?0)+(0?0)+(1?0)=0
    • 移位：A -> 00001101, B -> 00000111
  4. 第4次時鐘脈沖：
    • 取出當前位：A3 = 1, B3 = 0
    • 由于控制信號為1，B3取反：B3’ = 1
    • 全加器計算：𝑆3=1⊕1⊕0=0
    • 進位：𝐶4=(1?1)+(1?0)+(1?0)=1
    • 移位：A -> 00000110, B -> 00000011
  5. 第5次時鐘脈沖：
    • 取出當前位：A4 = 0, B4 = 1
    • 由于控制信號為1，B4取反：B4’ = 0
    • 全加器計算：𝑆4=0⊕0⊕1=1
    • 進位：𝐶5=(0?0)+(0?1)+(0?1)=0
    • 移位：A -> 00000011, B -> 00000001
  6. 第6次時鐘脈沖：
    • 取出當前位：A5 = 1, B5 = 0
    • 由于控制信號為1，B5取反：B5’ = 1
    • 全加器計算：𝑆5=1⊕1⊕0=0
    • 進位：𝐶6=(1?1)+(1?0)+(0?0)=1
    • 移位：A -> 00000001, B -> 00000000
  7. 第7次時鐘脈沖：
    • 取出當前位：A6 = 0, B6 = 0
    • 由于控制信號為1，B6取反：B6’ = 1
    • 全加器計算：𝑆6=0⊕1⊕1=0
    • 進位：𝐶7=(0?1)+(1?1)+(0?1)=0
    • 移位：A -> 00000000, B -> 00000000
  8. 第8次時鐘脈沖：
    • 取出當前位：A7 = 0, B7 = 0
    • 由于控制信號為1，B7取反：B7’ = 1
    • 全加器計算：𝑆7=0⊕1⊕0=1
    • 進位：𝐶8=(0?1)+(1?0)+(0?0)=0
結果

最終輸出結果的各位和為 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=00110010，即十進制的50。
image.png

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/14952.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/14952.shtml
英文地址，請注明出處：http://en.pswp.cn/web/14952.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

【最新區塊鏈論文錄用資訊】CCF A — SP 2024 共17篇

【最新區塊鏈論文錄用資訊】CCF A — SP 2024 共17篇

Conference：45th IEEE Symposium onSecurity and Privacy CCF level：CCF A Categories：網絡與信息安全 Year：2024 Num：17 Efficient Zero-Knowledge Arguments For Paillier Cryptosystem Paillier 加密系統的有效…
閱讀更多...
基于python的網頁自動刷新工具

基于python的網頁自動刷新工具

1.下載webdriver https://msedgewebdriverstorage.z22.web.core.windows.net/?prefix122.0.2365.59/下載Edge的瀏覽器驅動 2.安裝selenium pip install selenium4.11.1 3.寫代碼 # -*- coding: utf-8 -*- import tkinter as tk from tkinter import messagebox import thr…
閱讀更多...
【halcon】set_part 實現平移和縮放 徹悟版

【halcon】set_part 實現平移和縮放 徹悟版

背景 之前寫了一篇關于set_part 的文章 ，確實也實現了平移和縮放。平移是對的，但是縮放其實有畸變。這個問題一直都困擾著我，知道昨天連續測試了好幾個小時，直到晚上11點終于完美解決。 坐標和高寬 坐標 再講set_part 之前&am…
閱讀更多...
免費擼gpt-4o和各種大模型實用經驗分享

免費擼gpt-4o和各種大模型實用經驗分享

項目 Github: https://github.com/MartialBE/one-api 先貼兩張圖： 說明 免費擼AI大模型,各位可以對照下面我給出的大模型記錄表來填，key需要自己去拿，國內都需要手機號驗證，如果你不介意。另外我在自己的博客放出免費API給大家…
閱讀更多...
模型評價指標筆記：混淆矩陣+F1+PR曲線+mAP

模型評價指標筆記：混淆矩陣+F1+PR曲線+mAP

評價指標 二分類評價指標 混淆矩陣 TP: 正確預測為了正樣本，原來也是正樣本 FN: 錯誤的預測為負樣本，原來是正樣本 (漏報，沒有找到正確匹配的數目) FP: 錯誤的預測為正樣本，原來是負樣本 (誤報，沒有的匹配不正確) TN…
閱讀更多...
CIM模型

CIM模型

CIM 是 Esri 制圖信息模型。 它是一個地圖內容規范，用于記錄在保存、讀取、引用或打開時如何永久保留描述不同項目組件的信息。 該規范以 JSON 表示，適用于 ArcGIS 應用程序和 API 中的地圖、場景、布局、圖層、符號和樣式。 CIM 不僅限于制圖設置。 要了解屬性的組織方式以及…
閱讀更多...
【Tools】SpringBoot工程中，對于時間屬性從后端返回到前端的格式問題

【Tools】SpringBoot工程中，對于時間屬性從后端返回到前端的格式問題

Catalog 時間屬性格式問題一、需求二、怎么使用 時間屬性格式問題 一、需求 對于表中時間字段，后端創建對應的實體類的時間屬性需要設定格式（默認的格式不方便閱讀），再返回給前端。 二、怎么使用 導入jackson相關的坐標&#x…
閱讀更多...
How can I tell which package an executable came from? @ubuntu apt

How can I tell which package an executable came from? @ubuntu apt

apt-file search /usr/bin/mpifort
閱讀更多...
Vue.js - Vue 的安裝 以及 常用的 Vue 指令 【0基礎向 Vue 基礎學習】

Vue.js - Vue 的安裝 以及 常用的 Vue 指令 【0基礎向 Vue 基礎學習】

文章目錄 Vue 快速上手1、Vue.js 官網 & Vue.js 的獲取2、創建 Vue 實例，初始化渲染3、插值表達式 安裝 Vue 開發者工具：裝插件調試 Vue 應用Vue 指令1、v-show 指令2、v-if3、v-else & v-else-if4、v-onv-on 調用傳參 5、v-bindv-bind 對于樣式…
閱讀更多...
【算法】前綴和算法——和為k的子數組之和

【算法】前綴和算法——和為k的子數組之和

題解：和為k的子數組之和(前綴和算法) 目錄 1.題目2.題解思路2.1前綴和 哈希表，算法步驟：2.2細節如下：2.3參考代碼： 3.總結及思考 1.題目 題目鏈接：LINK 2.題解思路 暴力求解自然不用多說，時…
閱讀更多...
【SQL】外連接 LEFT JOIN

【SQL】外連接 LEFT JOIN

目錄 一.內連接與外連接 1.內連接（inner join） 2.外連接（outer join） 二.兩表連接 1.我們先來試試看內連接： 2.我們再來試試外連接 三.單表外連接 四.總結 一.內連接與外連接 先得介紹內連接和外連接兩個概念&…
閱讀更多...
第199題｜關于函數的周期性問題｜函數強化訓練（六）｜武忠祥老師每日一題 5月24日

第199題｜關于函數的周期性問題｜函數強化訓練（六）｜武忠祥老師每日一題 5月24日

解題思路：解這道題我們要用到下面這個結論 f(x)連續，以T為周期時，原函數以T為周期的充分必要條件是： (A) sin x顯然是以π為周期的，我們可以看到并不等于0,根據結論，A的原函數顯然不是周期函數。 (B) 的…
閱讀更多...
memmove使?和模擬實現

memmove使?和模擬實現

一：memmove的使? 這是memmove在庫里的定義，具體可在cplusplus.com查看 void * memmove ( void * destination, const void * source, size_t num ) ? 和memcpy的差別就是memmove函數處理的源內存塊和?標內存塊是可以重疊的。 ? 如果源空間和?標…
閱讀更多...
你以為的私域是真正的私域嘛？？你的私域流量真的屬于你嘛？

你以為的私域是真正的私域嘛？？你的私域流量真的屬于你嘛？

大家好 我是一個軟件開發公司的產品經理 專注私域電商行業7年有余 您的私域流量是真正的屬于你自己嘛？ 私域的定義 私域的界定：一個互聯網私有數據（資產）積蓄的載體。這個載體的數據權益私有，且具備用戶規則制定權…
閱讀更多...
Mysql 備份恢復 mysqldump與xtrabackup備份

Mysql 備份恢復 mysqldump與xtrabackup備份

1.1 備份的原因 備份是數據安全的最后一道防線，對于任何數據丟失的場景，備份雖然不一定能恢復百分之百的數據 (取決于備份周期)，但至少能將損失降到最低。衡量備份恢復有兩個重要的指標：恢復點目標(RPO) 和恢復時間目標(RTO)&…
閱讀更多...
數據庫常用命令（1）

數據庫常用命令（1）

DML 1.添加數據（insert into） insert into 表名 values (值1，值2....); 表示成功運行： 2.修改數據（update） update 表名 set 字段名1值1，字段名2值2.....【where條件】 3.刪除數據&#xff0…
閱讀更多...
元年科技數據智能研發部負責人張亞東受邀為第十三屆中國PMO大會演講嘉賓

元年科技數據智能研發部負責人張亞東受邀為第十三屆中國PMO大會演講嘉賓

全國PMO專業人士年度盛會 北京元年科技股份有限公司數據智能研發部負責人張亞東先生受邀為PMO評論主辦的2024第十三屆中國PMO大會演講嘉賓，演講議題為“大模型時代，AI創新型工具提升項目管理效率”。大會將于6月29-30日在北京舉辦，敬請關注&a…
閱讀更多...
jmeter之HTTP請求和查看結果樹

jmeter之HTTP請求和查看結果樹

一、HTTP請求作用： 可以發送post或get請求等請求可以向服務器發送參數或消息體數據可以進行文件上傳 HTTP請求：是線程組內的取樣器最常用的的一個原件 二、查看界面 添加一個HTTP請求：選擇線程組–添加–取樣器–HTTP請求 默認界面 名稱和…
閱讀更多...
ThreadLocal為什么會導致內存泄漏？

ThreadLocal為什么會導致內存泄漏？

問題引出： ThreadLocal是為了解決什么問題而產生的？ ThreadLocal發生內存泄漏的根本原因是什么？ 如何避免內存泄漏的發生？定義 為了解決多個線程同時操作程序中的同一個變量而導致的數據不一致性的問題。 ??假設現在有兩個線程A…
閱讀更多...
如何獲取一個城市或者一個區域的玫瑰風向圖？

如何獲取一個城市或者一個區域的玫瑰風向圖？

玫瑰風向圖是一種直觀展示風向和風速的圖形工具，它在氣象學、城市規劃、農業等領域都有廣泛的應用。那么，如何獲取某個城市或某個區域的玫瑰風向圖呢？ 首先，我們可以借助互聯網資源獲取玫瑰風向圖。現代網絡技術發達，…
閱讀更多...
最新文章

Copyright @ 2022~2023