題解：和為k的子數組之和(前綴和算法)

1.題目

題目鏈接：LINK

2.題解思路

暴力求解自然不用多說，時間復雜度是O(N^2)

可以用前綴和算法來進行求解，但是要做適當的轉換。

2.1前綴和 + 哈希表，算法步驟：

首先，我們在遍歷的時候要按照以i位置為結尾的子數組進行遍歷。

第二，要與前綴和相結合
我們要求的是和為k的子數組，可以轉換為誰前綴和為sum[i] - k

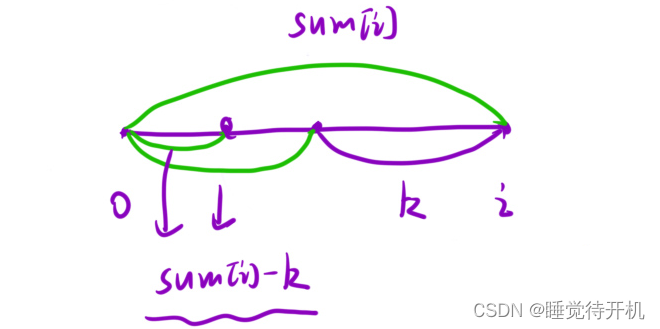
第三，我們計算出前綴和如果挨個遍歷前綴和數組來找誰等于sum[i] - k的話時間復雜度還是O(N^2)，因而我們要借助哈希表把每次找sum[i] - k值從O(N) 降到O(1)

2.2細節如下：

2.3參考代碼：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash; // 統計前綴和出現的次數hash[0] = 1;int sum = 0, ret = 0;for (auto x : nums) {sum += x;             // 計算當前位置的前綴和int target = sum - k; // 本次我們哈希表中要找的目標值if (hash.count(target))ret += hash[target]; // 統計個數hash[sum]++; // 將該次前綴和入到哈希表中，供下次使用}return ret;}
};

3.總結及思考

我感覺這個題目解法好難理解，雖然這個方法可行，但是還是有一些地方我感覺不太明白。

1.為什么不能用雙指針(滑動窗口來做)？
因為這個題目數組 不具有單調性(有負數)， 兩個指針不能一直同向移動。不滿足滑動窗口的使用前提條件。

2.為什么要將以i為開始的子數組轉換為以i為結尾的子數組？？？
因為要 為下一步使用前綴和做鋪墊

3.為什么要將前綴和數組用一個變量來替代？
因為 下一次所用的前綴和具有規律性，不用存著不需要的值

4.為什么要借助哈希表？
因為要 把每次找sum[i] - k的值的時間復雜度從O(N) --> O(1)

---

EOF