一、哈夫曼樹

1.1 哈夫曼樹的概念

給定一個序列，將序列中的所有元素作為葉子節點構建一棵二叉樹，并使這棵樹的帶權路徑長度最小，那么我們就得到了一棵哈夫曼樹（又稱最優二叉樹）

接下來是名詞解釋：

• 權：節點的數值
• 路徑長度：兩節點間路徑的邊數
• 帶權路徑長度：節點的權值乘以該節點到根節點的路徑長度即為該節點的帶權路徑長度。哈夫曼樹的帶權路徑長度是樹中所有葉子節點的帶權路徑長度之和。

例如下面這棵哈夫曼樹：

通過觀察我們可以發現，所有父節點的權值都是自身的兩個子節點的權值之和。而為了要使樹的帶權路徑長度最小，我們要盡可能的讓權值小的節點離根節點遠，讓權值大的節點離根節點近。

因此，我們引出哈夫曼樹的構造算法。

1.2 哈夫曼樹的構造算法

要將一個序列構造成一棵哈夫曼樹，我們首先需要對其進行升序排序

將排序好后的序列中的每個值看作一棵只有一個節點的樹，從中選出根節點權值最小的兩棵樹作為新樹的左右子樹，并將這兩棵樹從序列中刪除，而新樹的根節點的權值是這兩棵樹根節點的權值之和

哈夫曼樹沒有規定左右子樹的順序，因此下面的例子中將10和18的位置對調也是正確的

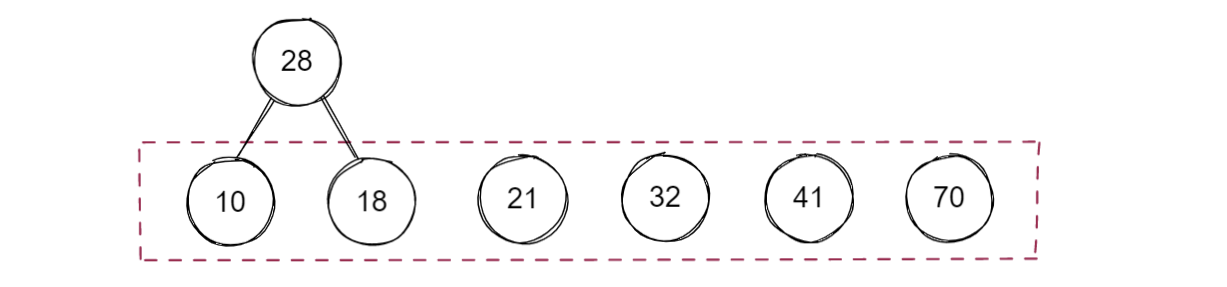
將新樹的根節點的權值放入序列中并重新進行升序排序，重復上述步驟

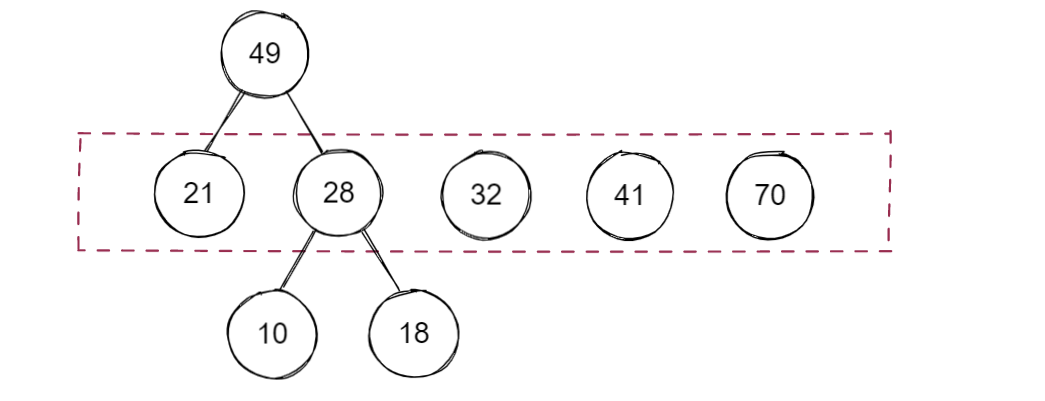
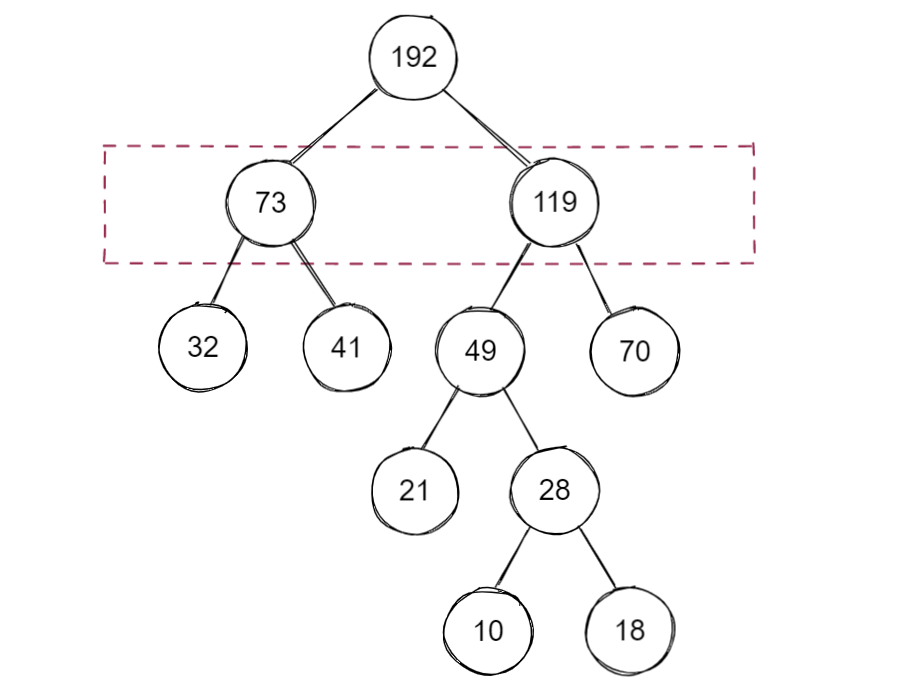
至此，就構建了一棵哈夫曼樹

因為哈夫曼樹沒有規定左右子樹的順序，因此一個序列可以構建出不同的哈夫曼樹

二、哈夫曼編碼

2.1 等長編碼

假設我們要對一個字符串ABAACDC進行二進制編碼

我們可以按順序給每個字符設置一個編碼，A為0，B為1，C為10，D為11

那么就可以將上面的字符串轉化為0100101110

但是在解碼的時候我們會發現，這一串二進制序列可以解碼為ACACDBA、ACABABDA等字符串，出現了歧義。

這是因為我們在對字符進行編碼的時候，出現了一個字符是另一個字符的前綴的情況，例如D可以用兩個B來表示。

為了避免歧義，我們可以采用等長編碼的方案，就是每個字符的編碼都一樣長，例如A為00，B為01，C為10，D為11，這樣就不會產生歧義了。

但是這種方案并不是一個最短的方案。

2.2 哈夫曼編碼

統計字符出現的次數，把字符定義成一個節點，節點的權值就是它出現的次數。

例如上面A出現了3次，B出現了1次，C出現了2次，D出現了1次

哈夫曼編碼的核心思想就是讓出現次數越多的字符編出來的碼越短，我們將全部節點構建成一棵哈夫曼樹，出現次數越少的字符對應的節點就越靠近樹的底層，編碼也就越長，出現次數越多的字符編碼就越短。

對二叉樹的邊標號，向左的邊標為0，向右的邊標為1，至此所有字符的編碼就是從根節點到該字符節點路徑上經過的標號，例如A為1，B為010，C為00，D為011，這種編碼方案就叫做哈夫曼編碼。

構建哈夫曼樹的時候，所有的字符節點都是葉子節點，不會出現一個字符出現在另一個字符的路徑上，也就不會出現一個字符是另一個字符的前綴這種造成歧義的情況

哈夫曼樹的編碼不是唯一的，節點放置的左右也會造成字符編碼的不同，但是生成的編碼長度一定都是一樣的。

完.