🔥 個人主頁：空白詩

🚀 引言

快速排序（Quick Sort）是一種高效的排序算法，由計算機科學界的傳奇人物托尼·霍爾（Tony Hoare）于1960年巧妙地提出。這一算法的核心智慧在于運用了經典的分治法策略——猶如古代兵法中的“分而治之”，將一個錯綜復雜的大列表分割成兩個相對簡單的子列表，隨后對這兩個子列表施以同樣的策略，直到每個子列表都只剩下單一元素或為空，此時整個序列自然歸于有序。此過程宛如構建一座秩序井然的金字塔，自下而上，層層推進。

---

📌 快速排序算法核心思想

1. 選擇基準值（Pivot）

這是算法流程的起點，從數列中精心挑選出一個元素，賦予它一個特殊角色——“基準”（pivot）。基準的選擇可以很靈活，但理想情況下應傾向于選擇一個能將數據集大致均勻分割的值，以促進算法效率。

2. 分區操作（Partitioning）

分區操作是快速排序的精髓所在。其目標是在遍歷數列一次的過程中，通過交換元素位置，使得所有小于基準值的元素都位于基準之前，而所有大于基準值的元素都排列在其后，相等的元素可以放置在任一側，完成這一操作后，基準值恰好位于其最終排序后的位置，即序列的中間。這一巧妙劃分不僅為后續遞歸奠定了基礎，也直接體現了快速排序分而治之的哲學。

3. 遞歸排序子序列

基于分區結果，數列被明確劃分為兩個獨立的部分：左側全部小于基準值，右側則大于基準值。接下來，算法會對這兩個子序列遞歸地應用同樣的排序邏輯。通過不斷地將問題規模減半，直到每個子序列只剩下一個或零個元素（這時自然視為已排序），整個數列便會在這一系列遞歸調用中逐步構建出全局的有序狀態。這一策略確保了快速排序高效利用了分治策略的優勢，尤其是在平均情況下展現出極高的效率。

---

📌 JavaScript 實現

1. 快速排序主函數

function quickSort(arr, left = 0, right = arr.length - 1) {// 如果左指針小于右指針，說明還有未排序的區間if (left < right) {// 調用分區函數，返回pivot的索引，完成一次分區const pivotIndex = partition(arr, left, right);// 對pivot左邊的子數組進行快速排序quickSort(arr, left, pivotIndex - 1);// 對pivot右邊的子數組進行快速排序quickSort(arr, pivotIndex + 1, right);}// 返回排序后的數組，實際上由于是原地排序，此處return并非必要return arr;
}

2. 分區函數

function partition(arr, left, right) {// 選擇最右側元素作為基準值pivotconst pivot = arr[right];let i = left; // i為小于pivot的元素的邊界，初始時指向最左側// 遍歷除了pivot外的所有元素for (let j = left; j < right; j++) {// 如果當前元素小于或等于pivotif (arr[j] <= pivot) {// 交換arr[i]和arr[j]，并將i右移一位，保持i左側的元素都小于等于pivot[arr[i], arr[j]] = [arr[j], arr[i]]; // ES6解構賦值進行交換i++; }}// 最后將pivot（arr[right]）與arr[i]交換，使得pivot位于正確的位置上[arr[i], arr[right]] = [arr[right], arr[i]];// 返回pivot的最終位置索引return i;
}

3. 示例代碼

// 未排序數組示例
const unsortedArray = [3, 6, 8, 10, 1, 2, 1];// 打印原始數組
console.log("Unsorted:", unsortedArray);// 調用快速排序函數，得到排序后的數組
const sortedArray = quickSort(unsortedArray);// 打印排序后的數組
console.log("Sorted:", sortedArray);

這段代碼實現了快速排序算法，通過quickSort函數遞歸地將數組分為更小的子數組，并通過partition函數完成每部分的排序，最終達到整個數組有序的目的。代碼中使用了ES6的解構賦值來簡化元素交換的操作，使得代碼更加簡潔易讀。

---

📌 優化建議

1. 三數取中法

• 核心思想：通過更智能地選擇基準值(pivot)來優化快速排序的性能。
• 操作步驟：
  1. 比較數組首部、中部、尾部的元素。
  2. 選取這三個數中的中位數作為分區操作的基準值。
  3. 這樣做能有效平衡劃分，即使在數據部分有序的情況下也能保持較好的性能，減少最壞情況的發生概率。

2. 小數組時切換排序算法

• 適用條件：當待排序序列的元素數量較少時（例如少于10或15個）。
• 策略詳情：快速排序在小數組上的優勢不明顯，此時切換到插入排序等簡單排序算法更為高效。因為插入排序在小數據集上具有較低的常數因子和無需遞歸的優點，能夠快速完成排序，與快速排序形成互補。

3. 尾遞歸優化

• 概念闡述：確保遞歸調用是函數的最后一個操作，便于某些支持該特性的編譯器進行優化。
• 實施方法：設計遞歸邏輯時，直接在遞歸調用的返回語句中返回計算結果，避免在遞歸返回后還需執行其他操作。
• 注意事項：雖然JavaScript等語言不一定能自動優化尾遞歸，遵循此原則編寫代碼依然有助于提高可讀性和未來跨平臺移植的兼容性。

4. 并行化處理

• 目標：利用多核CPU資源加速排序過程。
• 實施步驟：
  1. 將大數組分割成多個小塊。
  2. 各個CPU核心獨立并行地對分塊數據執行快速排序。
  3. 最后合并各塊已排序的結果。
• 優勢：在擁有多個處理器核心的系統上，此策略能顯著縮短排序時間，尤其適合處理海量數據。

通過上述一系列優化措施，快速排序算法不僅在理論上保持了較高的時間效率，在實際應用中也變得更加靈活和健壯，能夠有效應對各種規模數據集的排序挑戰，展現出更高的性能和穩定性。

---

📌 時間復雜度分析

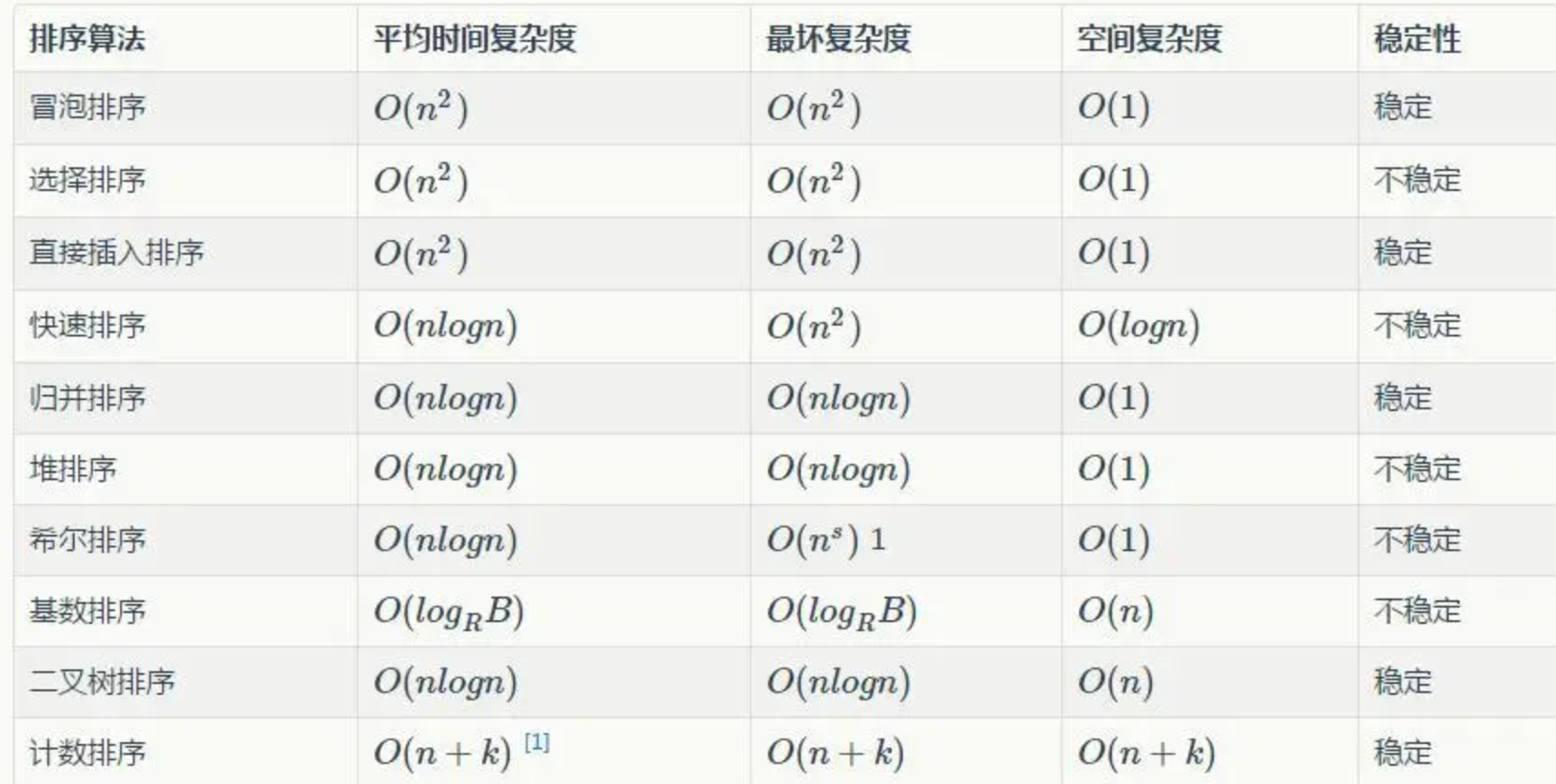
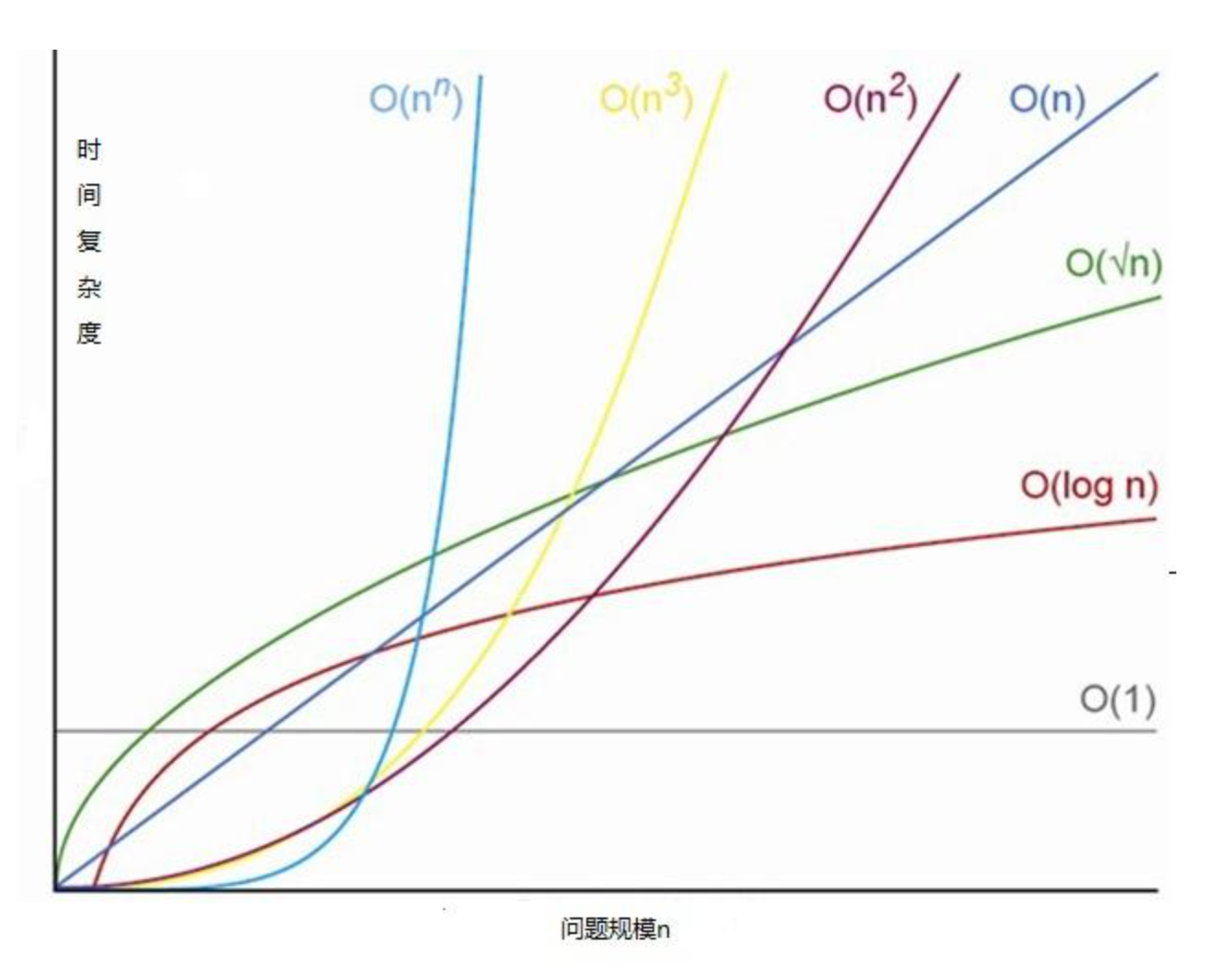
快速排序算法的性能極大程度上取決于基準值（Pivot）的選擇策略。

• 最優情況：若每次分區操作都能均勻地將數據集切分為兩部分，每部分包含近似相等數量的元素，則遞歸樹的深度為log?n。鑒于每一層遞歸涉及遍歷數組，總體操作計數約為n * log?n。因此，快速排序在最佳情況下的時間復雜度為O(n log n)，表現出高度的效率。

• 最差情況：相反，若每次選取的基準值都導致極不均衡的分區，極端情形下每次僅將數組分為一個元素和剩余所有元素兩部分，這將導致遞歸深度上升至n，伴隨每次遍歷數組的操作，時間復雜度惡化為O(n2)，與冒泡排序相近。

• 平均情況：在實踐中，若假定分區大致均勻，即每次都能將數據集分為兩個大小相似的子集，快速排序的平均時間復雜度同樣為O(n log n)。這對于多數隨機分布數據集而言，是一個非常高效的排序方案。

鑒于最壞情況下的性能瓶頸，實際部署快速排序算法時，往往配合采用基準值優化策略，比如“三數取中法”，來增強其魯棒性和普遍適用性，確保在多種數據條件下仍能保持高效的排序性能。

---

📌 總結

快速排序算法通過分治法策略實現高效排序，其核心包括選擇基準值、分區操作及遞歸排序子序列三大步驟。為了進一步提升性能和適應不同場景，可采納諸如三數取中法優化基準選擇、小數組時切換至插入排序、尾遞歸優化及并行處理等策略。這些優化不僅能夠減少最壞情況出現的概率，還充分利用現代計算資源，使快速排序在實踐中表現得更為出色，成為處理大量數據排序任務的優選算法之一。

總之，快速排序憑借其高效與靈活性，在眾多排序算法中占據重要地位，廣泛應用于各種數據排序需求之中。

---