Java方法的遞歸
- 前言
- 一、遞歸的概念
- 示例
- 代碼示例
- 二、遞歸執行過程分析
- 代碼示例
- 執行過程圖
- 三、遞歸練習
- 代碼示例
- 按順序打印一個數字的每一位(例如 1234 打印出 1 2 3 4)
- 遞歸求 1 + 2 + 3 + ... + 10
- 寫一個遞歸方法,輸入一個非負整數,返回組成它的數字之和. 例如,輸入 1729, 則應該返回1+7+2+9,它的和是19
- 求斐波那契數列的第 N 項
- 斐波那契數列介紹
前言
Java方法的遞歸是指一個Java方法直接或間接地調用自身,以完成重復或嵌套的計算任務。遞歸常用于處理具有自相似性的問題,通過分解問題為更小、更簡單的子問題來解決整個問題。遞歸方法需要明確定義遞歸終止條件,以防止無限循環。
一、遞歸的概念
一個方法在執行過程中調用自身, 就稱為 “遞歸”.
遞歸相當于數學上的 “數學歸納法”, 有一個起始條件, 然后有一個遞推公式.
遞歸是一種在方法內調用自身的編程技術。在使用遞歸時,方法會重復調用自身,每次調用時傳遞不同的參數,直到滿足某個終止條件為止。
遞歸可以用于解決一些問題,特別是那些具有遞歸結構的問題。在這些問題中,解決方案可以通過將問題分解為更小的子問題來實現。每次遞歸調用都會處理一個子問題,直到達到基本情況,然后將子問題的解決方案組合起來得到原始問題的解決方案。
遞歸要求在每次調用時,傳遞給遞歸方法的參數應該與原始問題的參數有關,但規模更小。這樣可以確保遞歸在每次調用時朝著基本情況前進,并最終達到終止條件。
遞歸的基本思想是將一個大問題分解為一個或多個相同類型的小問題,然后解決每個小問題,并將它們的解決方案組合起來得到原始問題的解決方案。遞歸方法必須有一個基本情況,以便在基本情況下終止遞歸調用。
在Java中,遞歸可以用于解決各種問題,例如計算階乘、斐波那契數列、遍歷樹等。但需要注意的是,遞歸可能會導致棧溢出的錯誤,因為每次遞歸調用都會將方法的調用信息存儲在棧中。因此,遞歸需要謹慎使用,并確保有適當的終止條件。
示例
求 N!
起始條件: N = 1 的時候, N! 為 1. 這個起始條件相當于遞歸的結束條件.
遞歸公式: 求 N! , 直接不好求, 可以把問題轉換成 N! => N * (N-1)!
代碼示例
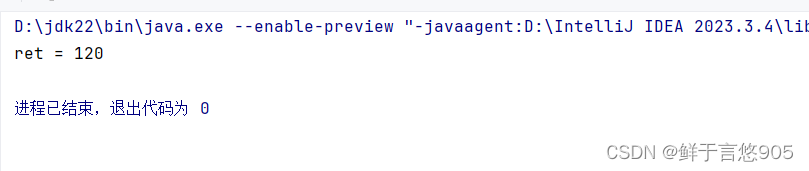
遞歸求 N 的階乘
class Main{public static void main(String[] args) {int n = 5;int ret = factor(n);System.out.println("ret = " + ret);}public static int factor(int n) {if (n == 1) {return 1;}return n * factor(n - 1); // factor 調用函數自身}
}
二、遞歸執行過程分析
遞歸的程序的執行過程不太容易理解, 要想理解清楚遞歸, 必須先理解清楚 “方法的執行過程”, 尤其是 “方法執行結束之后, 回到調用位置繼續往下執行”.
代碼示例
遞歸求 N 的階乘, 加上日志版本
class Main{public static void main(String[] args) {int n = 5;int ret = factor(n);System.out.println("ret = " + ret);}public static int factor(int n) {System.out.println("函數開始, n = " + n);if (n == 1) {System.out.println("函數結束, n = 1 ret = 1");return 1;}int ret = n * factor(n - 1);System.out.println("函數結束, n = " + n + " ret = " + ret);return ret;}
}
執行過程圖
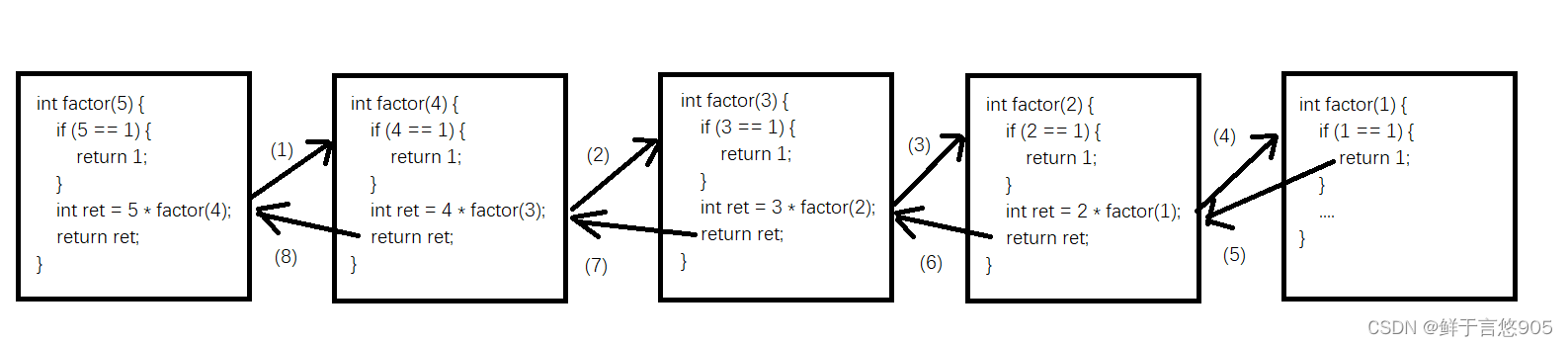
程序按照序號中標識的 (1) -> (8) 的順序執行.
關于 “調用棧”
方法調用的時候, 會有一個 “棧” 這樣的內存空間描述當前的調用關系. 稱為調用棧.
每一次的方法調用就稱為一個 “棧幀”, 每個棧幀中包含了這次調用的參數是哪些, 返回到哪里繼續執行等信息.
三、遞歸練習
代碼示例
按順序打印一個數字的每一位(例如 1234 打印出 1 2 3 4)
public static void print(int num) {if (num > 9) {print(num / 10);}System.out.println(num % 10);}
遞歸求 1 + 2 + 3 + … + 10
public static int sum(int num) {if (num == 1) {return 1;}return num + sum(num - 1);}
寫一個遞歸方法,輸入一個非負整數,返回組成它的數字之和. 例如,輸入 1729, 則應該返回1+7+2+9,它的和是19
public static int sum(int num) {if (num < 10) {return num;}return num % 10 + sum(num / 10);}
求斐波那契數列的第 N 項
斐波那契數列介紹
斐波那契數列是一個數學上的數列,其形式為 1, 1, 2, 3, 5, 8, 13, 21, 34, …。數列中的每個數字都是前面兩個數字之和。也就是說,第三個數字是前兩個數字之和,第四個數字是前兩個數字之和,以此類推。
斐波那契數列最早由13世紀的意大利數學家斐波那契(Fibonacci)發現和研究,他在其著作《算盤書》中介紹了這個數列,并將其應用于兔子繁殖的模型中。
斐波那契數列在數學中有著重要的應用和性質。它在自然界中也有許多出現的現象,例如植物的葉子排列、螺旋殼的形狀等都可以用斐波那契數列來描述。
斐波那契數列也有一些有趣的特性,例如當數列中的數字趨近無窮時,相鄰兩個數字的比值會趨近于黃金分割比例0.618。這個黃金分割比例在藝術和設計中也有廣泛的應用。
斐波那契數列除了以上的介紹,還有其他的許多性質和應用,它在數學中被廣泛研究和討論。
public static int fib(int n) {if (n == 1 || n == 2) {return 1;}return fib(n - 1) + fib(n - 2);}
當我們求 ?b(40) 的時候發現, 程序執行速度極慢. 原因是進行了大量的重復運算.
class Main {public static int count = 0; // 這個是類的成員變量. 后面會詳細介紹到.public static void main(String[] args) {System.out.println(fib(40));System.out.println(count);}public static int fib(int n) {if (n == 1 || n == 2) {return 1;}if (n == 3) {count++;}return fib(n - 1) + fib(n - 2);}
}
可以使用循環的方式來求斐波那契數列問題, 避免出現冗余運算.
class Main {public static int count = 0; // 這個是類的成員變量. 后面會詳細介紹到.public static void main(String[] args) {System.out.println(fib(40));System.out.println(count);}public static int fib(int n) {int last2 = 1;int last1 = 1;int cur = 0;for (int i = 3; i <= n; i++) {cur = last1 + last2;last2 = last1;last1 = cur;}return cur;}}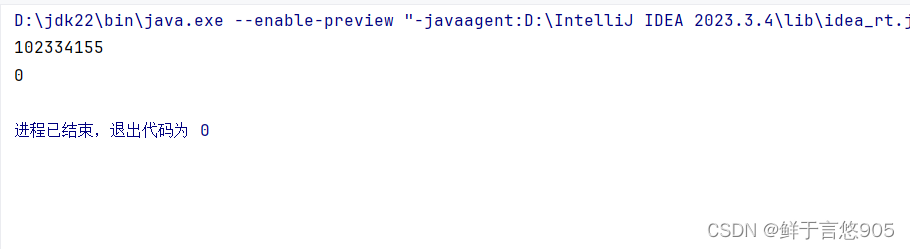










)
)
測試方法)


)

html 列表、有序列表、無序列表、列表嵌套)

