104. 二叉樹的最大深度

題目: 給定一個二叉樹 root ，返回其最大深度。

二叉樹的 最大深度 是指從根節點到最遠葉子節點的最長路徑上的節點數。

示例:

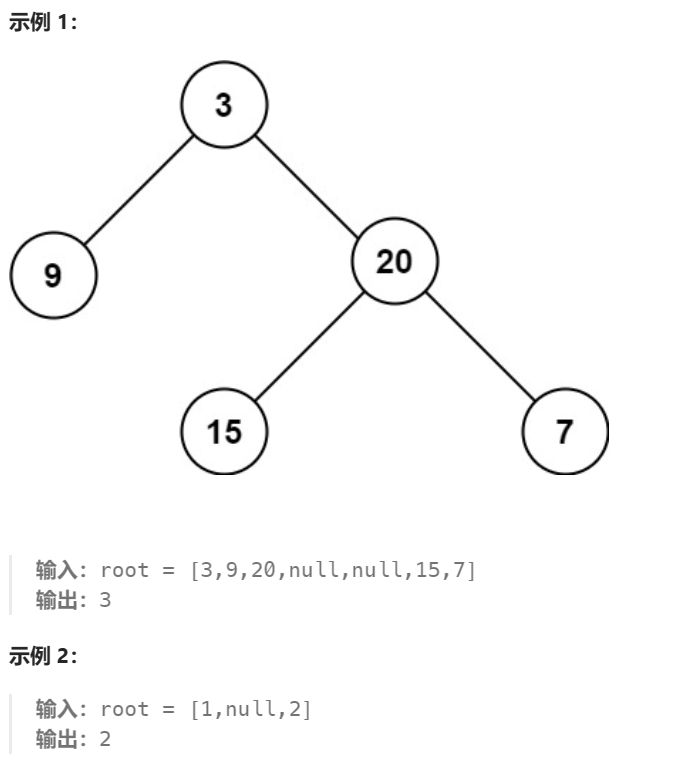
解題思路

• 沒有左右子節點的節點，稱為葉子節點

node->left ==nullptr && node->right ==nullptr`

• 葉子節點所在的層數，就是從跟節點到葉子節點的距離
• 統計遍歷所有節點，找到葉子節點
  • 如果當前節點不是葉子節點，則判斷該節點左節點或右節點是否葉子節點
  • 記錄每個葉子節點，所在層數，找到最遠距離的葉子節點

c++ 實現

class Solution {
public:int ans =0;void dfs(TreeNode* root, int level){if (root ==nullptr) return;if(root->left==nullptr && root->right==nullptr){ans = max(ans,level);}dfs(root->left,level+1);dfs(root->right,level+1);}int maxDepth(TreeNode* root) {dfs(root,1);return ans;}
};

• 定義dfs函數，傳入節點以及所在的層level; 因為當前節點所在的層等于跟節點到該節點的距離，可以用level來表示距離
• 首先從跟節點root開始遍歷，對應的level為1；
• 如果到達葉子節點，則更新最遠距離ans
• 然后接著從root->left開始，以及root->right開始尋找葉子節點，當前節點所在層為level+1
• 最終遍歷完所有節點，找到最遠距離ans

94. 二叉樹的中序遍歷

題目: 給定一個二叉樹的根節點 root ，返回 它的 中序 遍歷 。
示例:

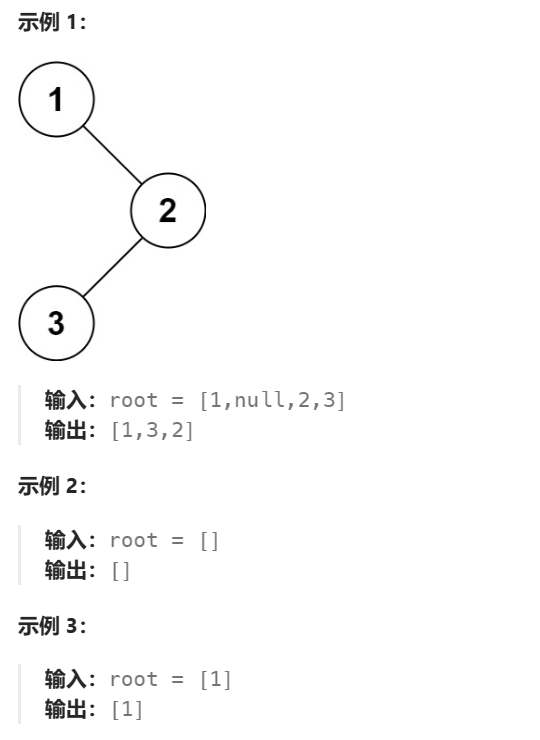
解題思路

• 中序遍歷: left -> root ->right(左中右)
• 遞歸遍歷，首先考慮dfs

c++ 實現

class Solution {
public:vector<int> ans;void dfs(TreeNode* root){if (root==nullptr) return;dfs(root->left);ans.push_back(root->val);dfs(root->right);}vector<int> inorderTraversal(TreeNode* root) {dfs(root);return ans;}
};

• 完整c++ 調試代碼

#include <iostream>
#include <vector>
using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x):val(x),left(nullptr),right(nullptr) {};
};class Solution {
public:vector<int> inorderTraversal(TreeNode* root){vector<int> result;inorder(root,result);return result;}
private:void inorder(TreeNode* root, vector<int>& result){if (root == nullptr) return;inorder(root->left,result);result.push_back(root->val);inorder(root->right,result);}
};int main()
{// 示例二叉樹: 1 /   \ 2     3// 創建二叉樹TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);// 使用中序遍歷函數Solution solution;vector<int> inorderTraversalResult = solution.inorderTraversal(root);// 打印結果for (int val:inorderTraversalResult){cout << val << " ";}// 清理內存delete root->left;delete root->right;delete root;return 0;
}

101. 對稱二叉樹

題目: 給你一個二叉樹的根節點 root ， 檢查它是否軸對稱。
示例:

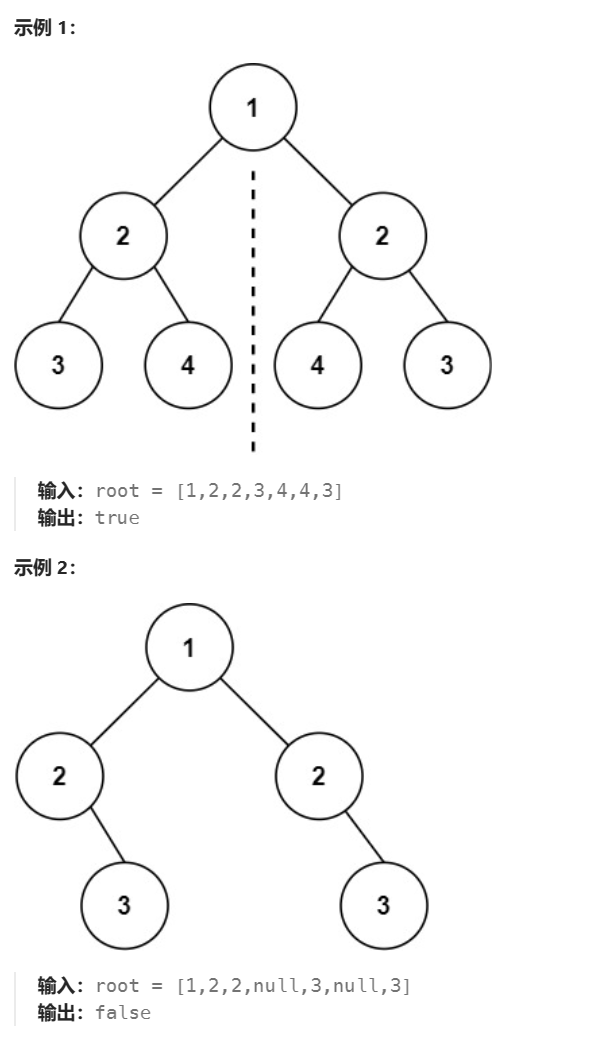
解題思路

觀察對稱二叉樹，查找滿足對稱的條件,可以發現

• 對稱樹，它的子節左右對稱，因此子節點需相同（如圖紅色的2和2）
• 同時，子節點的孫子節點，左右兩側也要滿足對稱，即 left_tree->left = right_tree->right; left_tree->right = right_tree->left;
• 找到規律后,遞歸遍歷二叉樹，判斷二叉樹是否對稱。

參考：https://www.cnblogs.com/itdef/p/14400148.html

c++ 實現

class Solution {
public:bool dfs(TreeNode* l,TreeNode* r){//遍歷到最后,都沒有找到不相等的節點，那么就是對稱的if(l==nullptr && r==nullptr) return true;if(l==nullptr && r !=nullptr) return false;if(l!=nullptr && r==nullptr) return false;if(l->val !=r->val) return false;// if(l->val ==r->val) return true; // 如果加了這一句，則這棵樹遍歷到存在左右節點相同，就不繼續向下遍歷了，因此不要加return dfs(l->left,r->right) && dfs(l->right,r->left); }bool isSymmetric(TreeNode* root) {return dfs(root->left,root->right);}
};

• 如果遍歷過程中，左右存在任意不相等的，則直接判斷不是對稱樹
• 如果遍歷到最后，都沒有發現不相等。因為已經到樹的最后，此時 l->left 與r->right都為空，而且l->right和l->left也都是空, 根據if(l==nullptr && r==nullptr) return true;此時dfs(l->left,r->right) && dfs(l->right,r->left)返回true
• 注意不要加:if(l->val ==r->val) return true, 不然遍歷不到樹的最后，只要在中間節點存在滿足這一要求的，就停止判斷了，無法對整棵樹進行判斷。

96. 不同的二叉搜索樹

題目: 給你一個整數 n ，求恰由 n 個節點組成且節點值從 1 到 n 互不相同的 二叉搜索樹 有多少種？``返回滿足題意的二叉搜索樹的種數。
示例:

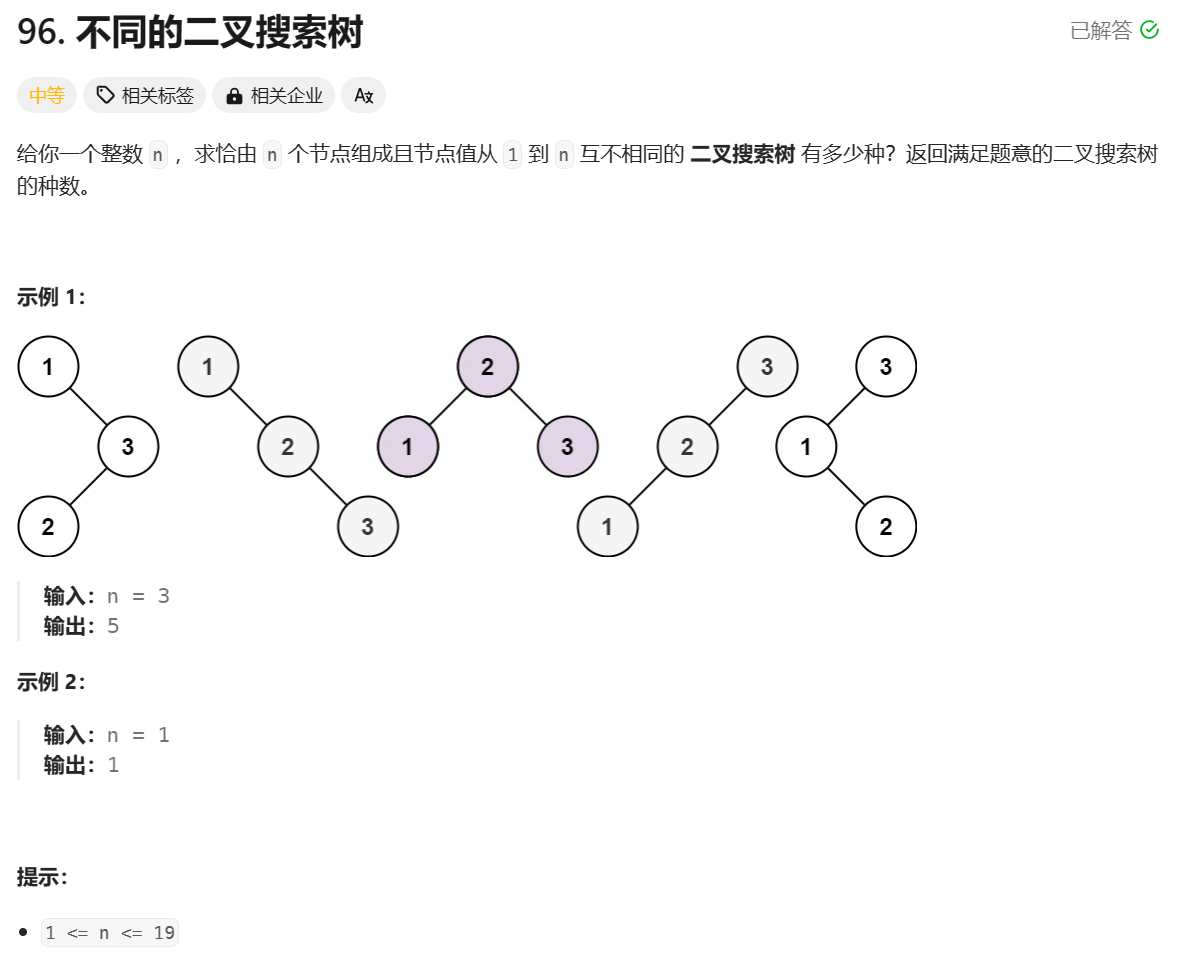
解題思路

二叉搜索樹, 也稱二叉排序樹或二叉查找樹。具有下列性質的二叉樹：

• 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值；
• 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值；
• 它的左、右子樹也分別為二叉排序樹。
• 二叉搜索樹作為一種經典的數據結構，它既有鏈表的快速插入與刪除操作的特點，又有數組快速查找的優勢；

• 使用動態規劃dp的方法求解, 設dp[n]記錄n個連續節點(從 1 到 n 互不相同)組成的二叉搜索樹的種類。
• 二叉搜索樹，左子樹上的所有節點均小于它的跟節點，右子樹上的所有節點均大于它的跟節點。
• 可知dp[1]為1， 因為只有一個節點，排列的可能就只有一種；另外dp[0]也為1，因為也只有一種排列可能。dp[2] 可組成兩種不同的搜索二叉樹，因此dp[2]=2
  
• 對于3個節點，列出了所有的不同的搜索二叉樹, 總共有5種。
  • 如果1作為根節點,由于找不到比跟節點小的數作為左子樹，因為左子樹為空(dp[0])， 此時2,3兩個節點在右子樹上存在2種搜索二叉樹的可能，也就是dp[2]：如果2在右子樹上，那么3由于比2大，那么3只能是它的右子節點。如果3在右子樹上，由于2比3小，2只能是它的左子節點); 此時種類數為: dp[0] * dp[2] = 2
    
  • 如果2作為跟節點, 因為1比跟節點2小，1只能是它的左節點，由于3比2大，3只能是根節點2的右節點, 因此只有1種可能：因此種類計算為 dp[1]*dp[1] =1
  • 如果3作為跟節點，由于沒有比它大的數，所以右子樹為空，也就是dp[0]，剩下的兩個數字都在左子樹上，對應為dp[2]: 如果1作為跟節點3的左節點，那么剩下的2只能是1的右節點(2比1大)；如果2作為跟節點3的左子節點，那么剩下的1只能是2的左子節點(1比2小)。因此種類計算為 dp[2]*dp[0] =2
  • 所以對于3個節點來說，所有的二叉樹為: dp[0] * dp[2] + dp[1]*dp[1] + dp[2]*dp[0] =5

因此得出如下規律：

• (1)遍歷每個數，作為根節點
• (2) 計算該跟節點下，所有搜索二叉樹的種類：左子樹（種類）* 右字數（種類）
• (3) 最后將計算結果求和

c++ 實現

class Solution {
public:int numTrees(int n) {int dp[20]; memset(dp,0x0,sizeof(dp));dp[0] =1;dp[1] =1;// 遍歷p[i]for(int i=2;i<=n;i++){   // i個節點，元素值 <=i; 遍歷以每個節點作為跟節點for (int j=1;j<=i;j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};

• 首先初始化dp[20] , 并通過memset 置為0 ，因為n<=19, 初始化的大小足夠了。
• 其中:dp[0] 和dp[1] 都為1
• 通過遍歷 for(int i=2;i<=n;i++)來計算p[i]的值
• 對于i個節點，元素值 <=i; 遍歷以每個節點作為跟節點, 計算此時搜索二叉樹的種類

dp[j-1] * dp[i-j]

• 因為左節點元素小于根節點，所以為dp[j-1], 根據解題思路的總結，右節點對應為dp[i-j] , 因為j-1+i-j =i-1;

102. 二叉樹的層序遍歷

題目：給你二叉樹的根節點 root ，返回其節點值的 層序遍歷 。 （即逐層地，從左到右訪問所有節點）。

示例:

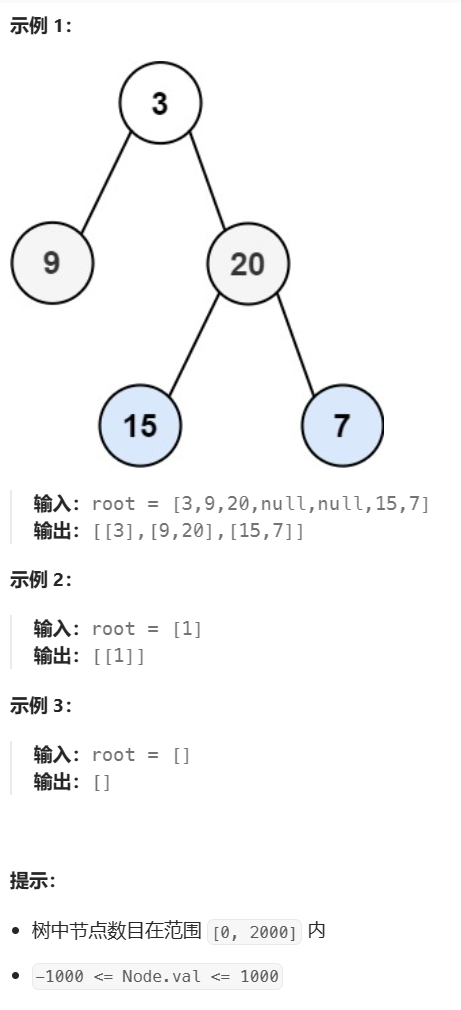
解題思路

BFS 廣度優先搜索算法的介紹，看出博文: BFS和DFS優先搜索算法

• BFS遍歷二叉樹 ，添加了遍歷的樹的層級level
• 根據層級決定新開vector或者直接push

• 先將跟節點root及層級0，加入到隊列queue中，然后遍歷隊列。
• 首先彈出根節點，并拿到節點值存儲到ans中
• 將根節點下一層子節點加入隊列
• 然后繼續彈出隊列中的節點，如果節點層級大于curr節點，增需要重新開一個vector,存儲該節點的值，如果和當前層級是一樣的，則直接push_back到vector中。
• 然后pop該節點，并將該節點的下一層子節點添加隊
• 繼續上述步驟，直到全部遍歷完。。。。

c++ 實現

class Solution {
public:vector<vector<int>> ans;int curr =0;       // current levelvector<int> v;     // 單個level 保存的結果void bfs(TreeNode* root){if(root==nullptr) return;//創建用來存儲節點和level的queuequeue<pair<TreeNode*,int>> q;// 放入第一個節點，同時記錄節點的層級q.push({root,0});while(!q.empty()){// 循環彈出需要處理的節點TreeNode* p=q.front().first;int level = q.front().second;// 記得從隊列中pop掉q.pop();// 如果處理的節點層級比當前vector層級更大// 那么說明上一層的節點數據已經處理完畢，需要重新開一個vector來記錄新的層級節點if(level>curr){// 更新curr 層級curr = level;// 將已經處理完畢的層級數據vector, 添加到ans結果中ans.push_back(v);// 得到一個空的vector, 用于記錄新的層級數據v.clear();v.push_back(p->val);}else{//如果處理節點的層級和當前curr層級一樣，直接push_back即可v.push_back(p->val);}// 將當前處理的節點的子節點，放入隊列中，注意要加上子節點所在的層級if (p->left !=nullptr) q.push({p->left,level+1});if (p->right !=nullptr) q.push({p->right,level+1});}// 記得將最后一次的結果v，加入ans中ans.push_back(v);return;}vector<vector<int>> levelOrder(TreeNode* root) {bfs(root);return ans;}
};

• 首先創建一個隊列queue來節點及所在level, 并插入根節點

//創建用來存儲節點和level的queue
queue<pair<TreeNode*,int>> q;
// 放入第一個節點，同時記錄節點的層級
q.push({root,0});

• 遍歷隊列，循環彈出需要處理的節點

// 循環彈出需要處理的節點TreeNode* p=q.front().first;int level = q.front().second;// 記得從隊列中pop掉q.pop();

• 如果處理的節點層級比當前vector層級更大，那么說明上一層的節點數據已經處理完畢，需要重新開一個vector來記錄新的層級節點

if(level>curr){// 更新curr 層級curr = level;// 將已經處理完畢的層級數據vector, 添加到ans結果中ans.push_back(v);// 得到一個空的vector, 用于記錄新的層級數據v.clear();v.push_back(p->val);}

• 如果處理節點的層級和當前curr層級一樣，直接push_back即可

 else{//如果處理節點的層級和當前curr層級一樣，直接push_back即可v.push_back(p->val);}

• 然后將pop掉的當前節點p的(下一層級)子節點加入隊列queue, 同時它的level+1

if (p->left !=nullptr) q.push({p->left,level+1});
if (p->right !=nullptr) q.push({p->right,level+1});

• 隊列遍歷完，記得將最后一次結果v加入到ans中

        // 記得將最后一次的結果，加入ans中ans.push_back(v);