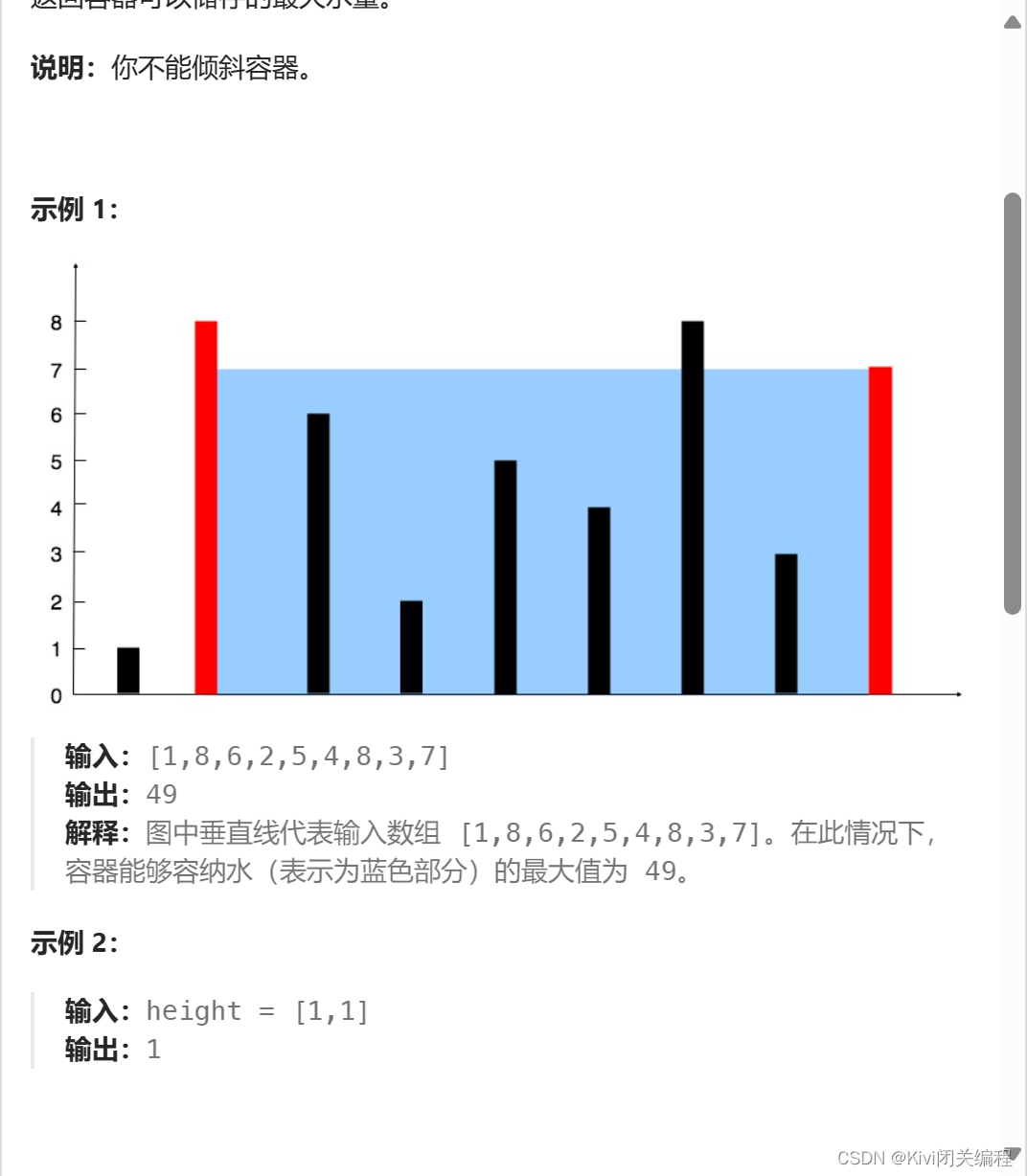
給定一個長度為 n 的整數數組 height 。有 n 條垂線,第 i 條線的兩個端點是 (i, 0) 和 (i, height[i]) 。
找出其中的兩條線,使得它們與 x 軸共同構成的容器可以容納最多的水。
返回容器可以儲存的最大水量。
提示:
n == height.length2 <= n <= 10^50 <= height[i] <= 10^4
解題思路:
定義兩個指針啊a,b分別指向height數組的第一個元素和第二個元素,表示容器的左邊和容器右邊,定義一個maxVolume表示記錄的最大容量,初始定義為0。定義兩層循環,外層循環a指針,內層循環b指針,如果當a,b指針所形成容器的容量大于maxVolume時更新maxVolume。遍歷完之后找到最大值。
class Solution {public int maxArea(int[] height) {int maxVolume = 0;for(int a=0;a<height.length;a++){for(int b=a+1;b<height.length;b++){if(((b-a)*Math.min(height[a],height[b]))>maxVolume)maxVolume = (b-a)*Math.min(height[a],height[b]);}}return maxVolume;}
}
時間復雜度為O(n^2),空間復雜度為O(1)。提交報錯:
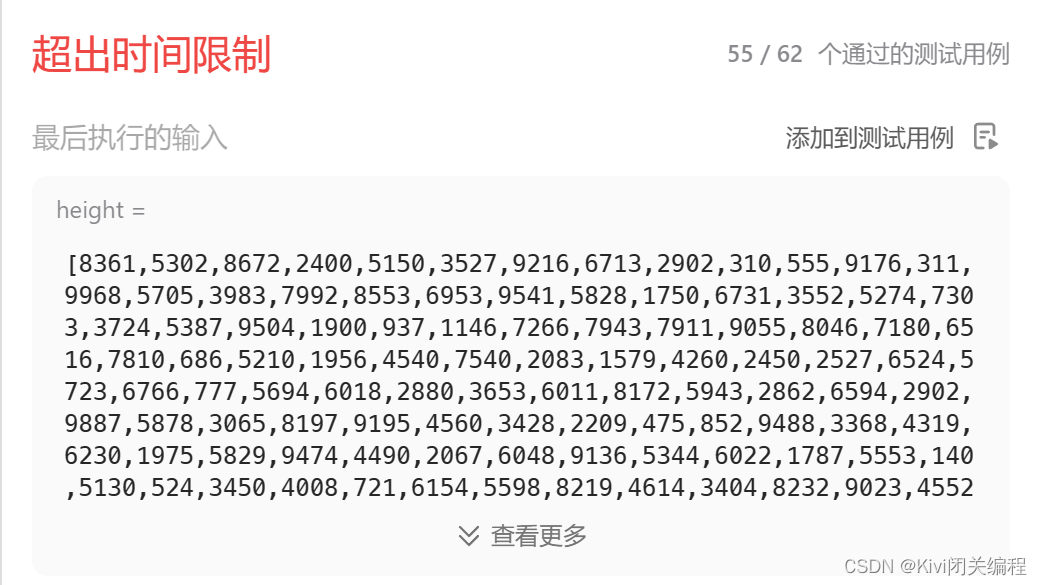
時間復雜度過高,得想辦法降低時間復雜度。
修改思路:
初始化定義兩個指針a,b分別指向height數組第一個元素和最后一個元素。初始化maxVolume等于height[a]*height[b]表示當前最大容量,分析一下可以知道,當前狀態的容量底寬是最寬的情況了,那么容量的大小,取決于左邊和后邊較矮的邊。例如如果當前是a,b所指高度是a所指高度較矮,那么要做到下一次找到的容器比原來的大,只能是找到一個更高的左邊才有可能。同理,如果是右邊更矮,則要找到一個更高的右邊才行。因此每次移動較矮的那一邊,如果是左邊更矮,則向右移,找到一個比原來左邊高的邊,重新計算容量;如果是右邊更矮,則向左移,找到一個比原來右邊高的邊。重新計算容量,如果比之前容量大,則更新maxVolume。直到左邊指針越過右邊指針,則停下。當前maxVolume是最大的容量。
代碼:
class Solution {public int maxArea(int[] height) {int a=0,b=height.length-1;int maxVolume=(b-a)*(Math.min(height[a],height[b]));int maxLeftEdge = height[a],maxRightEdge = height[b];while(a<b){if(height[a]<height[b]){a = a+1;while(height[a]<=maxLeftEdge&&a<b)a=a+1;}else{b = b-1;while(height[b]<=maxRightEdge&&a<b)b=b-1;}if((b-a)*(Math.min(height[a],height[b]))>maxVolume){maxVolume = (b-a)*(Math.min(height[a],height[b]));maxLeftEdge = height[a];maxRightEdge = height[b];}}return maxVolume;}
}
結果:
上述算法時間復雜度為O(n),空間復雜度為O(1)。
但是看到時間復雜度依然有改進空間。查看1ms時間復雜度的代碼:
class Solution {public int maxArea(int[] height) {int l =0,r =height.length-1;int max =0;while(l<r){if(height[r]>height[l]){max = Math.max(max,(r-l)*height[l]);int tmp = height[l];while(tmp>= height[l]&&l<r) l++;}else{max = Math.max(max,(r-l)*height[r]);int tmp = height[r];while(tmp>= height[r]&&l<r) r--;}}return max;}
}
觀察發現,總體代碼邏輯與我自己的一樣,不同點在于每次的maxVolume計算使用了Math.max(max,(r-l)*height[l]),同時是放在if語句中計算。同時只是使用一個臨時變量存儲之前左右邊高度。避免了重復的矮邊判斷。
總結
雙指針問題,較低時間復雜度解題的關鍵在于如何初始化指針位置以及找到如何移動指針的策略。例如這一題在于初始化指針為第一個元素和最后一個元素,同時分別找到最矮邊移動以計算最大值。我文章中的前一題,移動零問題,在于初始化指針都為數組開頭,然后移動一個指針尋找非零0,另一個指針定位下一個非零值存放的位置。






——布局、動畫與音樂)











)
