1.紅黑樹的概念
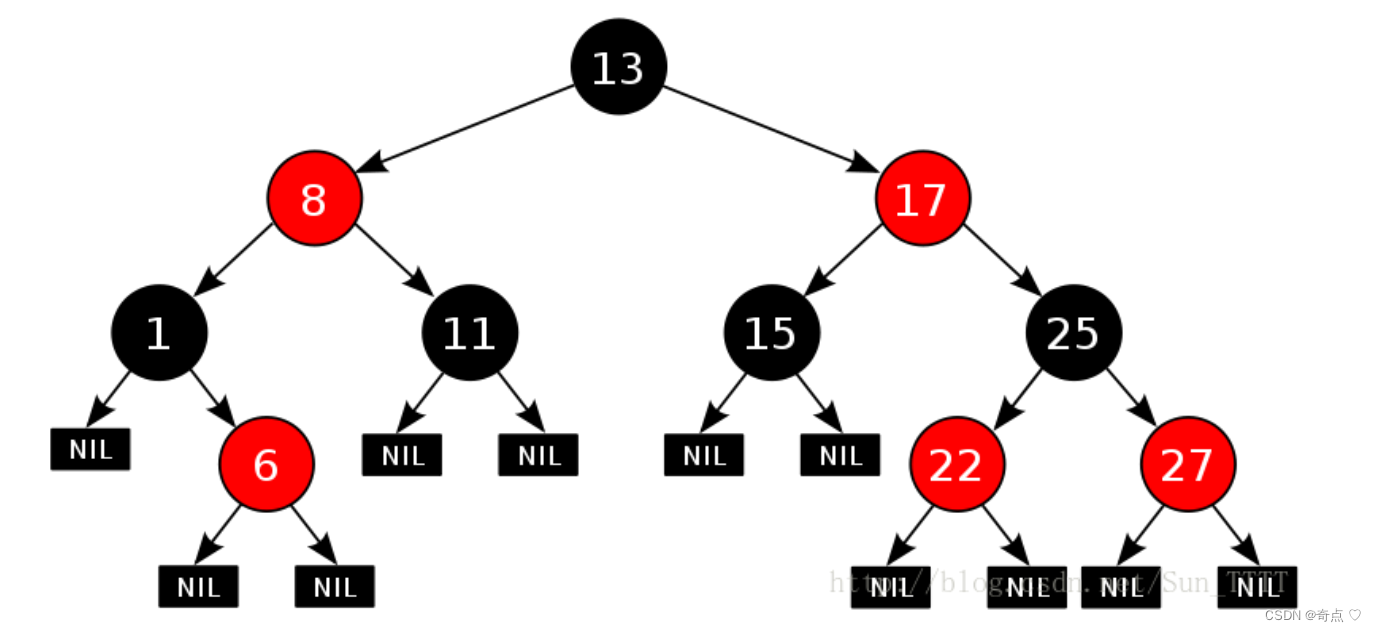
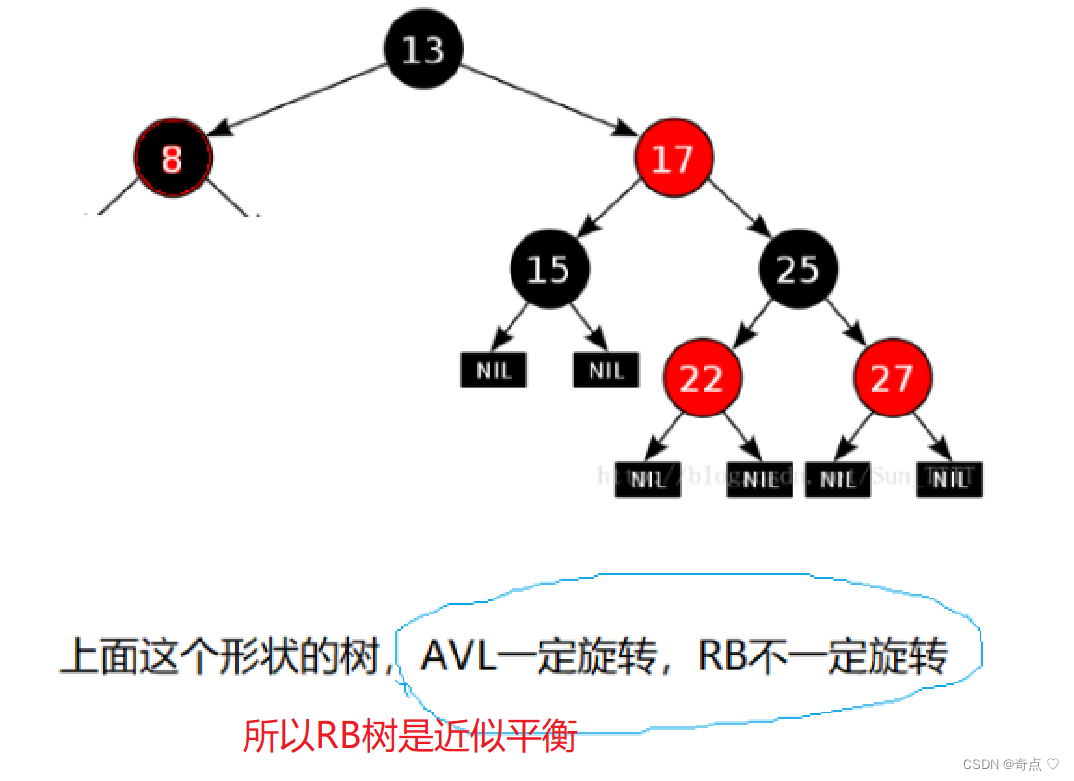
紅黑樹,是一種二叉搜索樹,但在每個結點上增加一個存儲位表示結點的顏色,可以是Red或
Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制,紅黑樹確保沒有一條路
徑會比其他路徑長出倆倍,因而是接近平衡的。
 ?
?
2.紅黑樹的性質?
1. 每個結點不是紅色就是黑色
2. 根節點是黑色的?
3. 如果一個節點是紅色的,則它的兩個孩子結點是黑色的 (沒有連續的紅色節點)
4. 對于每個結點,從該結點到其所有后代葉結點的簡單路徑上,均 包含相同數目的黑色結點?
5. 每個葉子結點都是黑色的(此處的葉子結點指的是空結點)NIF節點
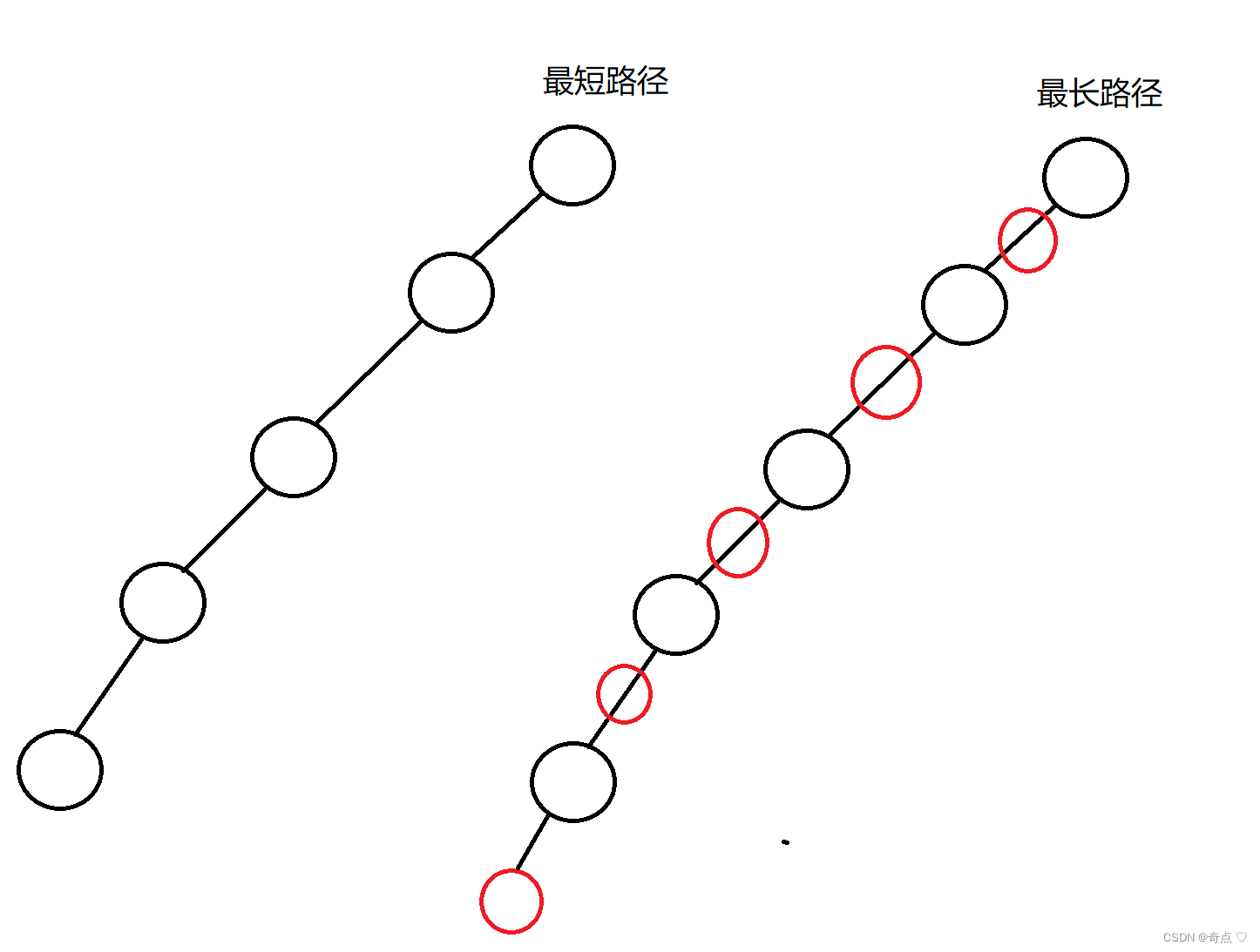
思考:為什么滿足上面的性質,紅黑樹就能保證:其最長路徑中節點個數不會超過最短路徑節點
個數的兩倍?看圖
路徑:從該節點到NIF節點
最短路徑:全黑節點
最長路徑:一黑一紅
?3.紅黑樹的平衡
節點定義
enum Color
{RED,BLACK,
};template<class K,class V>
class RBNode
{
public:typedef RBNode<K, V> Node;RBNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _col(RED), _kv(kv){}Node* _left;Node* _right;Node* _parent;Color _col;pair<K, V> _kv;//庫里面提供的結構體,表示key和value};顏色初始化必須是紅色,如果插入的是黑色,必定會影響每條路徑的黑色節點的數量,紅色的話只會影響該條路徑
插入
template<class K,class V>
class RBTree
{
public:typedef RBNode<K, V> Node;bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//...........}private:Node* _root = nullptr;
};插入分為三種情況(p為parent,g為grandparent,u為uncle)
cur一定為紅色了
1:p是黑色,不用處理
2:p是紅色,u存在且為紅色
3:p是紅色,u不存在或存在為黑色
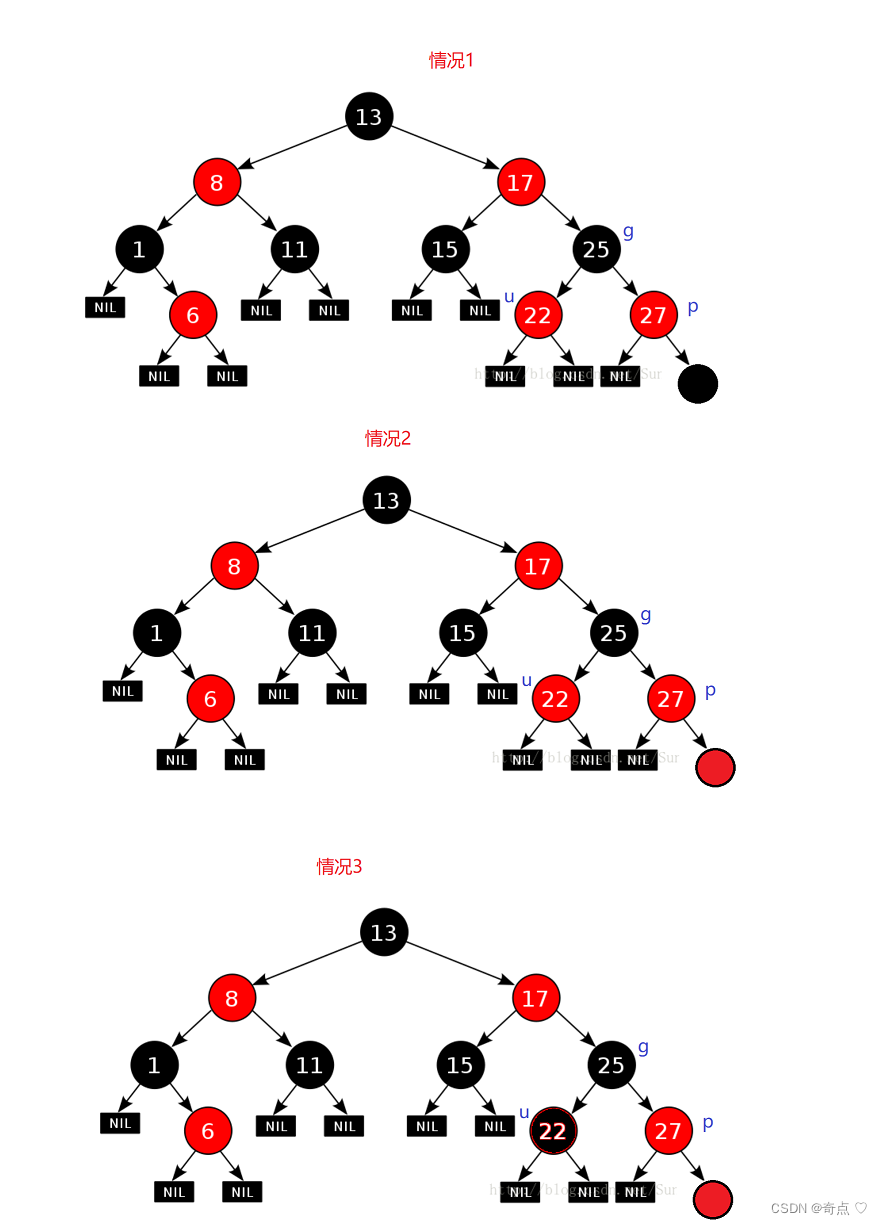
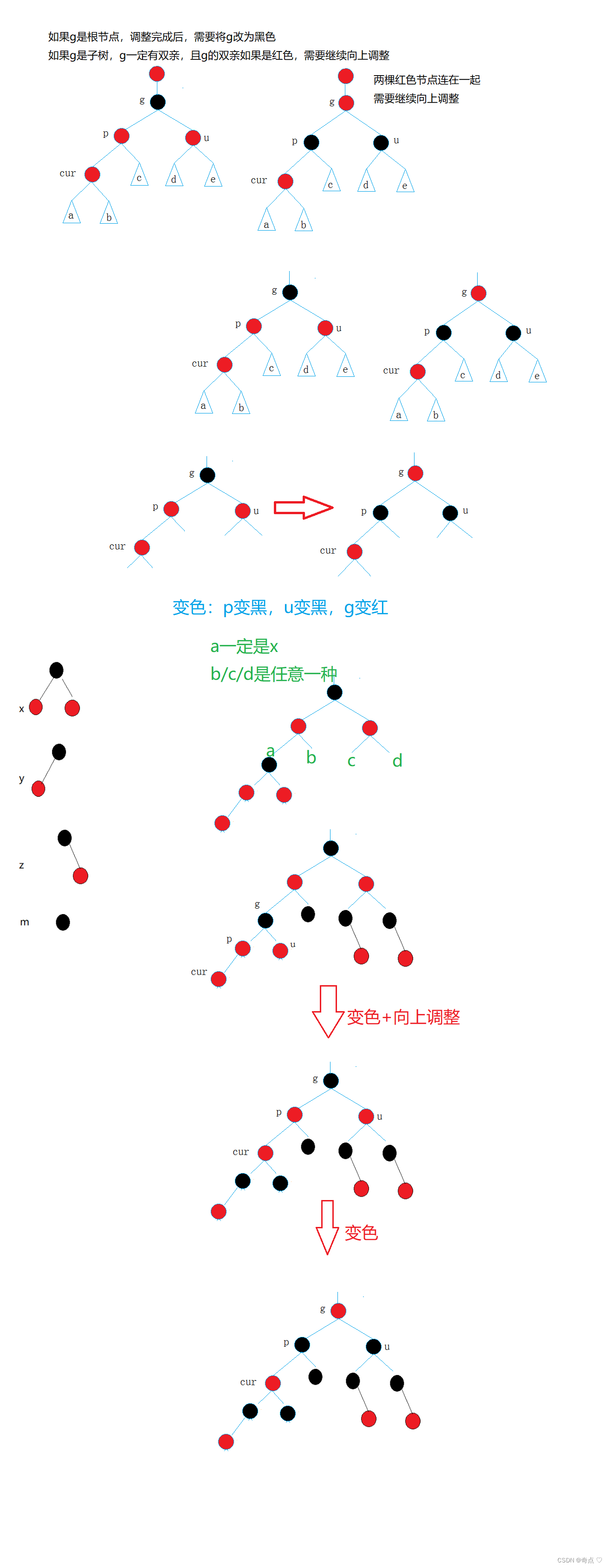
情況2:?
p是紅色,u存在且為紅色
變色+向上
 ?
?
情況3:
?p是紅色,u不存在或存在為黑色
u在右孩子時

u在左孩子同理?
下面是插入后面實現的代碼,里面有注釋
while(parent&&parent->_col == RED){Node* grandparent = parent->_parent;if (grandparent->_right == parent){Node* uncle = grandparent->_left;//情況1:u存在且為紅,變色加向上調整if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;//向上調整cur = grandparent;parent = cur->_parent;}else//情況2a:u不存在或者u存在且為黑 旋轉+變色{/* gu pc*///左單旋+變色if (parent->_right == cur){RotateL(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else{/* gu pc *///右單旋+左單旋+變色RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}else{Node* uncle = grandparent->_right;//情況1:u存在且為紅,變色加向上調整if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;//向上調整cur = grandparent;parent = cur->_parent;}else//情況2b:u不存在或者u存在且為黑 旋轉+變色{/* gp u c *///右單旋+變色if (parent->_right == cur){RotateR(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else{/* gp uc *///左單旋+右單旋+變色RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}_root->_col = BLACK;//管你變成什么色,根反正最后還是黑色return true;?4.紅黑樹的驗證
驗證是紅黑樹,就要滿足他的性質,首先不能出現連續紅色節點,其次每條路徑的黑色節點的數量要相等
不能出現連續紅色節點:不要用cur,然后和cur->孩子來比較,因為會有兩個孩子,比較麻煩,可以用cur->parent來比較
每條路徑的黑色節點的數量要相等:先算出一條路徑的黑色節點的數量,作為基準值,進行比較
bool IsRBTree(){if (_root && _root->_col == RED){cout << "根節點顏色是紅色" << endl;return false;}int nummark = 0;//給個黑色節點基準值,然后和它比較Node* cur = _root;while (cur){if(cur->_col == BLACK)nummark++;cur=cur->_left;}return _Check(_root, 0, nummark);}
bool _Check(Node* root, int blacknum, int nummark){if (root == nullptr){if (nummark != blacknum){cout << "某條路徑黑色節點的數量不相等" << endl;cout << blacknum << endl;return false;}return true;}if (root->_col == BLACK){blacknum++;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << "具有連續的紅色節點" << endl;return false;}return _Check(root->_left, blacknum, nummark)&& _Check(root->_right, blacknum, nummark);}void testRBTree()
{srand(time(0));const size_t N = 5000000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));}//t.Inorder();cout << t.IsRBTree() << endl;
}?


應用服務器優化技術有哪些)



|虛析構函數|重載函數|純虛函數|抽象類)
)
)





:CSS選擇器)




