?
目錄
一、算法效率
什么是算法
如何衡量一個算法的好壞
算法效率
二、時間復雜度
時間復雜度的概念
大O的漸進表示法
推導大O階方法
常見時間復雜度計算舉例??
三、空間復雜度
常見時間復雜度計算舉例
一、算法效率
什么是算法
算法(Algorithm):就是定義良好的計算過程,他取一個或一組的值為輸入,并產生出一個或一組值作為輸出。簡單來說:算法就是一系列的計算步驟,用來將輸入數據轉化成輸出結果。
如何衡量一個算法的好壞
下面求斐波那契數列的算法好還是不好,為什么?該如何衡量一個算法的好壞呢??
public static long Fib(int N){
if(N < 3){return 1;
}return Fib(N-1) + Fib(N-2);
}算法效率
算法效率分析分為兩種:第一種是時間效率,第二種是空間效率。
時間效率被稱為時間復雜度,而空間效率被稱作空間復雜度。
時間復雜度主要衡量的是一個算法的運行速度,而空間復雜度主要衡量一個算法所需要的額外空間。
在計算機發展的早期,計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展,計算機的存儲容量已經達到了很高的程度。所以我們如今已經不需要再特別關注一個算法的空間復雜度。?
二、時間復雜度
時間復雜度的定義:在計算機科學中,算法的時間復雜度是一個數學函數,它定量描述了該算法的運行時間。
那我們就在想:那程序運行,記為時間開始,程序結束,記為時間結束,兩者相減不就好了嘛?
這樣想是不對的。因為每臺電腦的性能都是不一樣的,處理程序的時間也會不一樣,就比如:老的電腦可能慢一點,新電腦可能快一點
時間復雜度的概念
?所以才有了時間復雜度這個分析方式。一個算法所花費的時間與其中語句的執行次數成正比例,算法中的基本操作的執行次數,為算法的時間復雜度。?
大O的漸進表示法
我們通過一段代碼學習大O的漸進表示法:?
// 請計算一下func1基本操作執行了多少次?
void func1(int N){int count = 0;
//下面這個for循環執行了N^2次
for (int i = 0; i < N ; i++) {for (int j = 0; j < N ; j++) {count++;}
}
//下面這個for循環執行了2*N次
for (int k = 0; k < 2 * N ; k++) {count++;
}int M = 10;
//下面這個while循環執行了10次
while ((M--) > 0) {count++;
}System.out.println(count);
}
分析思路:
第一個for循環,它是雙重循環,外圈從0開始,循環到N;內圈也從0開始,循環到N。所以循環了N*N=N^2次執行次數。
第二個for循環,他只有一層循環,按順序的循環,從0開始,循環了2*N次執行次數。
第三個for循環,他M是10,M--到0結束,執行了10次執行次數。????????
Func1 執行的基本操作次數 :
F(N)=N^2+2*N+10?
- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010?
實際中我們計算時間復雜度時,我們其實并不一定要計算精確的執行次數,而只需要大概執行次數,那么這里我們使用大O的漸進表示法。?
大O符號(Big O notation):是用于描述函數漸進行為的數學符號。
推導大O階方法
1、用常數1取代運行時間中的所有加法常數。
2、在修改后的運行次數函數中,只保留最高階項。
3、如果最高階項存在且不是1,則去除與這個項目相乘的常數。得到的結果就是大O階。?
所以對于上面那個代碼,我們算出執行次數的函數表達式為:F(N)=N^2+2*N+10;
對于方法1:F(N)=N^2+2*N+1;
對于方法2:F(N)=N^2+1;
對于方法3:F(N)=N^2+1;
而1對于這個函數來說,可以忽略不記,所以最后時間復雜度就為:O(N^2)
另外有些算法的時間復雜度存在最好、平均和最壞情況:
最壞情況:任意輸入規模的最大運行次數(上界)
平均情況:任意輸入規模的期望運行次數
最好情況:任意輸入規模的最小運行次數(下界)
例如:在一個長度為N數組中搜索一個數據x。最好情況:1次找到,最壞情況:N次找到
平均情況:N/2次找到
在實際中一般情況關注的是算法的最壞運行情況,所以數組中搜索數據時間復雜度為O(N)?
常見時間復雜度計算舉例??
【實例1】?
// 計算func2的時間復雜度?
void func2(int N) {int count = 0;
for (int k = 0; k < 2 * N ; k++) {count++;
}int M = 10;
while ((M--) > 0) {count++;
}System.out.println(count);
}所以對于上面那個代碼,我們算出執行次數的函數表達式為:F(N)=2*N+10;
對于方法1:F(N)=2*N+1;
對于方法2:F(N)=2*N+1;
對于方法3:F(N)=N;
所以最后時間復雜度就為:O(N);
【實例2】
// 計算func3的時間復雜度?
void func3(int N, int M) {int count = 0;
for (int k = 0; k < M; k++) {count++;
}
for (int k = 0; k < N ; k++) {count++;
}System.out.println(count);
}所以對于上面那個代碼,我們算出執行次數的函數表達式為:F(N)=M+N;
對于方法1:F(N)=M+N;
對于方法2:F(N)=M+N;
對于方法3:F(N)=M+N;
所以最后時間復雜度就為:O(M+N);
【實例3】
// 計算func4的時間復雜度?
void func4(int N) {int count = 0;
for (int k = 0; k < 100; k++) {count++;
}System.out.println(count);
}所以對于上面那個代碼,我們算出執行次數的函數表達式為:F(N)=100;
對于方法1:F(N)=1;
對于方法2:F(N)=1;
對于方法3:F(N)=1;
所以最后時間復雜度就為:O(1);
【實例4】
// 計算bubbleSort的時間復雜度?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;
}
}
if (sorted == true) {break;
}
}
}
注意!這時候可能會陷入個誤區:?兩層循環不就是array.length^(array.length-1)嗎?
但是你要想清楚,假設end=3,(注意看代碼,end每次循環都會變化,下面的循環也會變化)
第一次:end=3,i=1;i++;i=2;(i<end:3)
第二次:end=2,i=1;(i<end:2)
循環結束。
所以:執行次數為n-1.....n-2......n-3......1這是個等差數列求和(Sn=n(a1+an)/2);
所以F(N)=(N*(N-1))/2 = (N^2-N)/2
所以對于上面那個代碼,我們算出執行次數的函數表達式為:F(N)=(N^2-N)/2
對于方法1:F(N)=(N^2-N)/2;
對于方法2:F(N)=(N^2)/2;
對于方法3:F(N)=N^2;
所以最后時間復雜度就為:O(N^2);
【實例5】
/ 計算binarySearch的時間復雜度?
int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;
while (begin <= end) {int mid = begin + ((end-begin) / 2);
if (array[mid] < value)begin = mid + 1;
else if (array[mid] > value)end = mid - 1;
elsereturn mid;
}return -1;
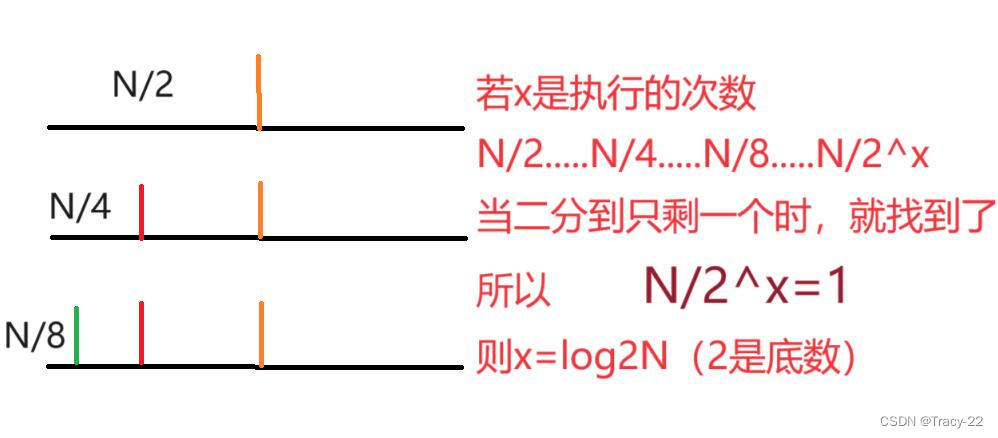
}?上面程序是二分查找,但是對于時間復雜度的求法有兩點:
1.看代碼
2.看思想
顯然,直接看代碼行不通,并不能很容易推斷出他的執行次數的函數。所以我們看下圖:
【實例6】
// 計算階乘遞歸factorial的時間復雜度?
long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;
}?遞歸的時間復雜度:遞歸的次數*每次遞歸后? 代碼執行的次數。
注意:只要不是循環等等,普通的代碼語句都是O(1);
上述代碼也是需要看思想的,這個是遞歸代碼,我們可以試試先帶個簡單的值,
比如:FIb(3):
Fib(3)執行一次--》Fib (2) 執行一次--》FIb(1)執行一次。
所以是O(N)
【實例7】
// 計算斐波那契遞歸fibonacci的時間復雜度?
int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
遞歸的時間復雜度:遞歸的次數*每次遞歸后? 代碼執行的次數。
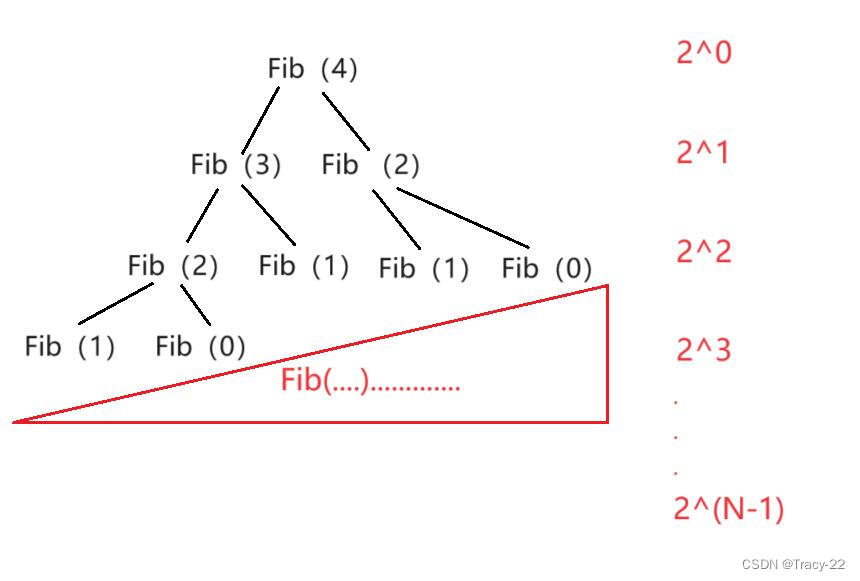
我們可以試試先把Fib(4)帶入,得下圖:
2^0+2^1+2^2+2^3+......+2^(N-1)? ?這是一個等比數列
等比數列公式為:Sn=a1 (1-q^n)/ (1-q);
則算出數據為:O(2^N)
?
 ?
?
那又會有一個想法:右下角那部分不是空缺了嗎?我們不是在完整的狀況下求的空間復雜度嗎?
答:空間復雜度我們一般都是求最壞的結果,所以即使多了一部分也無妨,反正求的是最壞的結果。?
三、空間復雜度
空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的量度 。空間復雜度不是程序占用了多少bytes的空 間,因為這個也沒太大意義,所以空間復雜度算的是變量的個數。空間復雜度計算規則基本跟時間復雜度類似,也使用大O漸進表示法。?
常見時間復雜度計算舉例
?【實例1】
// 計算bubbleSort的空間復雜度?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;
}
}
if (sorted == true) {break;
}
}
}我們的變量只有:end,sorted,i?這三個額外的空間。
可能會有個想法:為什么int[ ] array不算呢?
答:作為參數、條件傳入函數的都不算時間復雜度,因為不是臨時占用的空間也不是額外占用的空間。
即使是經歷了N次循環,但是要知道的是:空間是可以重復利用的。
比如:i被int出來,會進入局部域在這個棧幀里面創建一個,出了作用域(也就是括號)棧幀銷毀,空間釋放。下次再int的的i也是同一個空間,所以i只創建了一個變量。
只計算變量個數,不管變量類型,也不算空間具體的字節數。
所以上述代碼空間復雜度為:O(3)
又根據大O漸進階方法中:方法3:O(3)=O(1)
?【實例2】
// 計算fibonacci的空間復雜度?int[] fibonacci(int n) {long[] fibArray = new long[n + 1];fibArray[0] = 0;fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}return fibArray;
}上述代碼創建了 N+1 個大小的數組
而1可以直接省略,數值太小了忽略不計
所以空間復雜度為:O(N)
?【實例3】
// 計算階乘遞歸Factorial的空間復雜度?
long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;
}假設:我們N為3,Fib(3)--》Fib(2)--》Fib(1)一共三次
我們函數在每次執行時,都會在棧上開辟一份臨時的空間
所以空間復雜度為:O(N)
|虛析構函數|重載函數|純虛函數|抽象類)
)
)





:CSS選擇器)







)
ML模型實戰及經驗總結(更新中))

