---

📋 前言

在當今工業領域，圖思維方式與圖數據技術的應用日益廣泛，成為圖數據探索、挖掘與應用的堅實基礎。本文旨在分享嬴圖團隊在算法實踐應用中的寶貴經驗與深刻思考，不僅促進業界愛好者之間的交流，更期望從技術層面為企業在圖數據庫選型時提供新的視角與思路。

---

🎯 K鄰算法的實踐意義

K鄰算法（K-Hop Neighbor），即K跳鄰居算法，是一種基于廣度優先搜索（BFS）的遍歷策略，用于探索起始節點周圍的鄰域。該算法在關系發現、影響力預測、好友推薦等預測類場景中得到了廣泛應用。

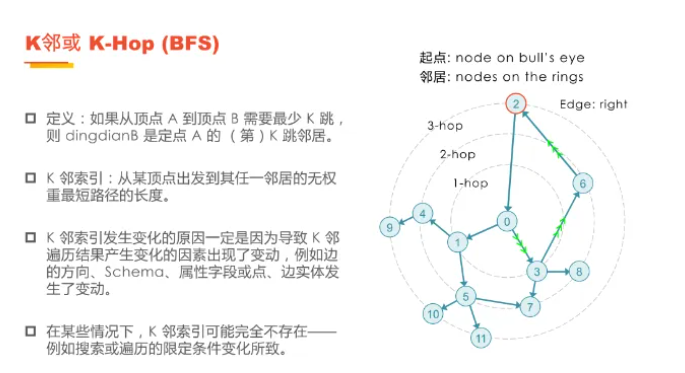
在圖論中，沿著一條邊移動被視為一跳（hop）。在遍歷圖中的頂點時，我們需要考慮多跳問題。圖論起源于數學家歐拉在1836年提出的哥尼斯堡七橋問題，它奠定了圖計算的數學基礎。自20世紀80年代以來，圖計算技術迅速發展，成為現代計算領域的重要組成部分。

在現實世界中，危機的傳播正是K鄰搜索的一個典型應用。以發生危機的實體為起點，順著或逆著（取決于邊的具體定義）邊的方向進行1步、2步、3步乃至更深層次的查詢，得到的就是先后會被危機波及到的實體。

以下是一個簡單的 JavaScript 示例，演示了如何使用K鄰近（K-Nearest Neighbors，KNN）算法進行分類。在這個示例中，我們將創建一個簡單的數據集，包含兩個特征（x和y坐標）和兩個類別（0和1），然后使用KNN算法對新數據進行分類。

// 定義數據集
const dataset = [{ x: 1, y: 2, label: 0 },{ x: 2, y: 3, label: 0 },{ x: 3, y: 4, label: 0 },{ x: 4, y: 5, label: 1 },{ x: 5, y: 6, label: 1 }
];// 定義一個函數來計算兩點之間的歐氏距離
function euclideanDistance(point1, point2) {const dx = point1.x - point2.x;const dy = point1.y - point2.y;return Math.sqrt(dx * dx + dy * dy);
}// 定義KNN分類函數
function knn(dataset, newPoint, k) {// 計算新數據點到數據集中每個點的距離const distances = dataset.map(data => ({point: data,distance: euclideanDistance(newPoint, data)}));// 根據距離排序數據點distances.sort((a, b) => a.distance - b.distance);// 取前k個最近的點const nearestNeighbors = distances.slice(0, k);// 統計最近鄰居中各類別的數量const counts = nearestNeighbors.reduce((acc, curr) => {const label = curr.point.label;acc[label] = (acc[label] || 0) + 1;return acc;}, {});// 找到最多的類別let maxCount = 0;let predictedLabel;for (const label in counts) {if (counts[label] > maxCount) {maxCount = counts[label];predictedLabel = label;}}return predictedLabel;
}// 測試新數據點的分類
const newPoint = { x: 3.5, y: 4.5 };
const k = 3;
const predictedLabel = knn(dataset, newPoint, k);
console.log(`新數據點 (${newPoint.x}, ${newPoint.y}) 的預測類別是：${predictedLabel}`);

🎯 創新應用與案例分析

以某知名房地產企業HD的供應鏈圖譜為例，我們可以通過持股方向、資金流向等信息，清晰直觀地揭示危機的傳播路徑和傳遞對象。

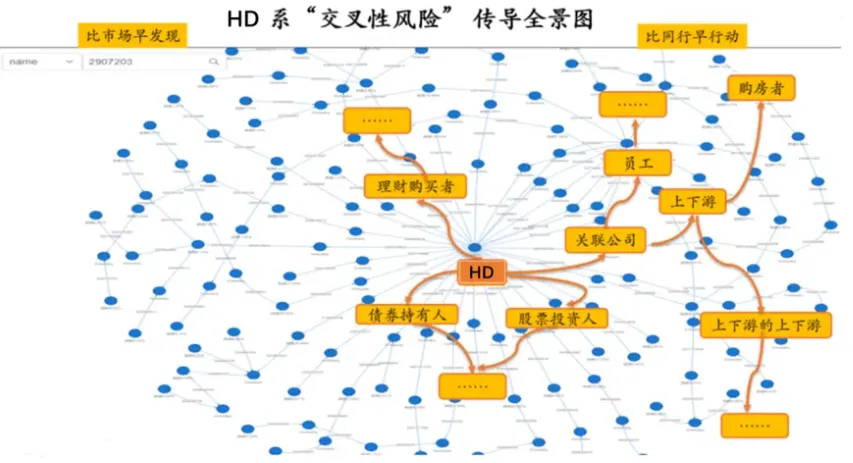
以HD為例，危機發生后，風險傳播路徑如下：

• 第一層：影響HD的關聯公司；
• 第二層：影響公司員工和供應商；
• 第三層：影響購房者（供應商停止供貨、工人停工，可能導致HD的在建工程停滯）。

風險從HD集團開始，逐步擴散至關聯公司、員工、供應商、購房者等，形成了一張復雜的“網絡”，呈現出明顯的“鏈條效應”。

然而，許多與風險傳導相關的實際應用并未采用圖計算，而是依賴于手工計算，如銀行KYC部門在計算UBO時仍使用Excel表。這種做法的效率和準確率可想而知。這與金融機構IT系統的陳舊和工作方法的落后有直接關系，阻礙了業務的開展，如企業影響力分析。

企業影響力分析不僅涉及持股關系、生產供求關系等傳統問題，還應包括與企業相關的所有金融行為和事件，以及與這些行為事件直接或間接相關的事務。分析的視角不應僅限于企業實體，而應擴展至企業發布的產品、債券等。

如下圖所示，分析的核心是企業的某個債券，其價格下跌可能直接影響其他債券的價格：

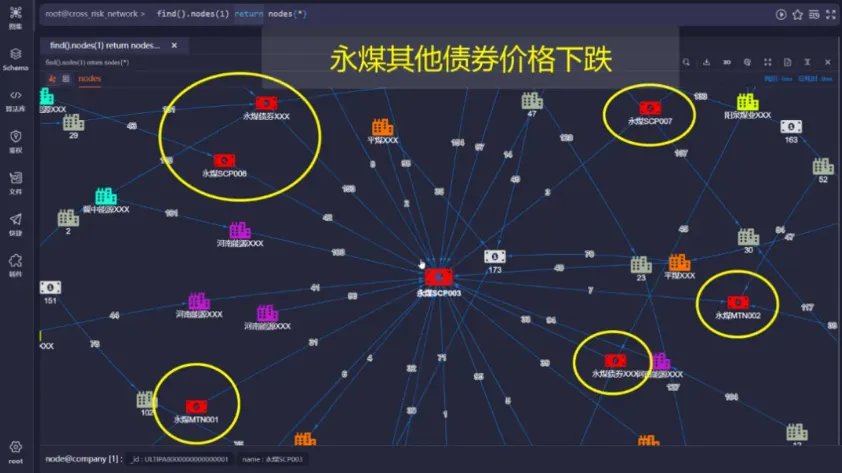
下圖則標出了持有該債券的、可能受影響的省內其他企業：

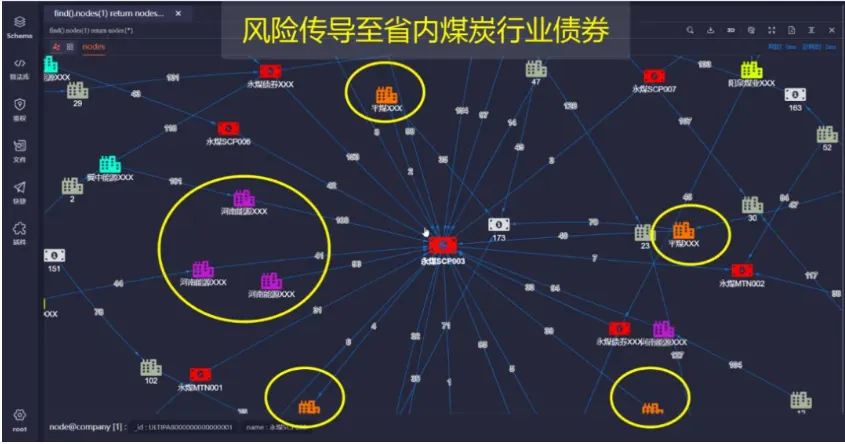
下圖展示的是該債券的1步鄰居，從這些鄰居繼續向外探尋就能得到該債券價格下跌后產生的危機傳遞效應：

專家們已越來越認識到，金融風險并不是孤立存在的，不同風險間具有鏈條效應，任何一只蝴蝶扇動翅膀，都有可能造成跨市場的風險傳染——風險的關聯性具有相互轉化、傳遞和耦合的特點——圖技術與蝴蝶效應在本質上是不謀而合的，即通過深度挖掘不同來源的數據，以網絡化分析的方式去洞察。

此外，金融場景是一種基于長鏈條計算的場景，這就導致技術實現時的規則更為復雜，因為會涉及到各種回溯、歸因，而且數據的計算量更大，同時也更注重時效性。只有實現真正的實時、全面、深度穿透、逐筆追溯、精準計量的監測和預警，才能保障金融風控中不會出現“蝴蝶效應”式的風險發生。

值得注意的是，圖往往包含著復雜的屬性及定義，例如：邊的有向、無向，邊的屬性權重，K 鄰是否包含 K-1 鄰，如何處理計算環路等等，這些問題會導致 K 鄰算法具體實現的差異。此外，在一些實際場景中，圖自身拓撲結構的變化，過濾條件的設定，節點、邊屬性的變化都會影響到 K 鄰計算的結果。

在行業應用中，K鄰算法通常應用于多模態的異構圖，即將多個單一信息的圖融合在一起形成的綜合性圖譜。這對算法實現者的數據收集和構圖能力提出了高要求，同時也對K鄰算法的靈活性和功能性提出了更高標準。嬴圖的高密度并發圖算法庫是目前全球運行最快、最豐富的圖算法集合，支持通過EXTA接口進行熱插拔和擴展。

如果在公開資料中看到K鄰算法的應用多是同構圖（只有一種點、一種邊），可能是因為作者想通過簡單的例子闡明觀點，或者因為構圖能力不足限制了算法的應用，也可能是K鄰算法的實現不盡人意，無法對異構圖進行恰當處理。K鄰算法的應用應該是廣泛且實際的，能夠解決現實問題的，如果是因為后面兩種情況而限制了算法的“大展宏圖”，那么相關圖廠商就應該反思一二并提高自身了！

最后，一個優秀的算法設計不僅應具備解決問題的能力，還應關注計算效率，即算力。我們列舉了一些高性能圖計算系統應具備的核心能力，以供企業在評估市場上各種圖計算產品時作為參考：

• 高速圖搜索能力：高QPS/TPS、低延時，實時動態剪枝能力；
• 對任何規模圖的深度、實時搜索與遍歷能力（10層以上）；
• 高密度、高并發圖計算引擎：極高的吞吐率；
• 成熟穩定的圖數據庫、圖計算與存儲引擎、圖中臺等；
• 可擴展的計算能力：支持垂直與水平可擴展；
• 3D+2D高維可視化、高性能的知識圖譜Web前端系統；
• 便捷、低成本的二次開發能力（圖查詢語言、API/SDK、工具箱等）。

---

🔥 參與方式

《圖算法：行業應用與實踐》免費包郵送出 3 本！

抽獎方式：隨機抽取 3 位小伙伴免費送出！
參與方式1：關注博主、點贊、收藏、評論區評論 （隨機有效留言即可）（切記要點贊+收藏，否則抽獎無效，每個人最多評論三次！）
參與方式2：關注博主公眾號，私信然后參與抽獎
活動截止時間：2024-5-18 22:00
當當網購買鏈接：https://product.dangdang.com/29705431.html