僅一個進程故障就無法達成共識
僅一個進程故障指的是在異步的分布式系統中
異步系統的共識問題(consensus)涉及一組進程,其中有的進程可能不可靠(unreliable)。共識問題要求可靠的進程一致地從兩個侯選中決定(agree)一個。本文表明解決該問題的任何協議都可能不終止,即使故障(faulty)進程只有一個。相比而言,同步系統的共識問題,即“拜占庭將軍”問題,已有解決方案。
一、簡介
在分布式計算中,達成遠程進程之間的一致性是最基本的問題之一,并且是許多分布式數據處理、分布式文件管理和容錯分布式應用程序算法的核心。
遠程進程之間達成一致的問題是分布式計算中最基本的問題之一,也是許多分布式數據處理算法、分布式文件管理和容錯分布式應用程序的核心問題。一個眾所周知的問題形式是“事務提交問題”,它在分布式數據庫系統中出現[6, 13, 15-17, 21-24](參見G. LeLann的私人通信,在[15]中引用)。問題是,所有參與處理特定事務的數據管理進程必須就是是否將事務的結果安裝到數據庫中或者丟棄它們達成一致的決定。如果由于某種原因一些數據管理進程無法執行所需的事務處理,可能需要執行后者操作。無論做出什么決定,所有數據管理者必須做出相同的決定,以保持數據庫的一致性。
共識問題的定義。
共識問題的例子:事務提交問題
實現“commit”問題所需的類型的協議對于參與進程和網絡完全可靠的情況來說是很簡單的。然而,真實的系統會遭受多種可能的故障,如進程崩潰、網絡分區以及丟失、失真或重復的消息。甚至可以考慮更多的拜占庭式的失敗[5,7,8,11,14,18,19],在這種情況下,有缺陷的進程可能會完全失控,甚至按照某種惡意計劃發送消息。因此,我們希望在面對這些故障時,擁有盡可能可靠的協議。當然,任何協議都可能被太頻繁或太嚴重的故障壓垮,所以我們所期望的是一個能夠容忍一定數量“預期”故障的協議。
希望能夠容忍一定數量的失敗
在這篇論文中,我們展示了一個令人驚訝的結果,**即沒有任何完全異步的共識協議能夠容忍即使一個未經通知的進程死亡的情況。**我們不考慮拜占庭故障,并且我們假設消息系統是可靠的,它可以正確地且僅一次地傳遞所有消息。然而,即使在這些假設下,一個進程在不適宜的時間停止運行可以導致任何分布式共識協議無法達成一致。因此,這個重要問題在沒有進一步關于計算環境的假設或對可容忍故障類型的更大限制的情況下沒有健壯的解決方案!
即使不考慮拜占庭失敗以及假設消息系統是可靠的,在這兩個前提下,仍舊不能達到一致
我們證明的關鍵是處理是完全異步進行的;也就是說,我們對處理器的相對速度或傳遞消息的延遲時間沒有任何假設。我們還假設進程無法使用同步時鐘,因此不能使用基于超時的算法。 (特別地,在[6]中的解決方案不適用。)最后,我們不假設可以檢測到進程的死亡,因此一個進程無法確定另一個進程是否已經死亡(完全停止)或者僅僅運行得很慢。
異步的定義:對處理器的相對處理速度或者傳遞消息的延遲沒有任何的假設。
假設沒有時鐘,沒有超時機制。
假設不能檢測進程的死亡。
我們的不可能性結果適用于共識問題的一個非常弱的形式。假設每個進程都從區間(0, 1)內的一個初始值開始。非故障進程通過進入適當的決策狀態來決定一個區間(0, 1)內的值。所有非故障進程在做出決策時都被要求選擇相同的值。為了證明不可能性,我們只需要最終某個進程做出決策。(當然,任何有興趣的算法都需要所有非故障進程做出決策。)對應于不同的初始配置,我們規定 0 和 1 都是可能的決定值;這就排除了類似“總是選擇 0”的簡單方案。
不可能性在非常弱的場景下都是成立的,那么在更復雜的現實情況下不可能性成立更是顯然的。
此外,論文只要求了某個正常的進程做出決策,并沒有要求所有的非故障進程都做出決策。一般的論文都是要求所有的非故障進程都要做出正確決策。
如果某個正常的進程都不能做出決策,那么也就是結論:沒有進程能夠做出正確決策。——這是一個更強的否定。
我們的系統模型非常強大,以盡可能廣泛地適用于我們的不可能性證明。進程被建模為自動機(可能有無限多個狀態),通過消息進行通信。在一個原子步驟中,進程可以嘗試接收消息,在基于消息是否被傳遞給它以及傳遞的消息是哪一個的基礎上進行局部計算,并將任意但有限數量的消息發送給其他進程。特別地,假設具有“原子多播”能力,以便一個進程可以在一步中將相同的消息發送給所有其他進程,并且知道如果有任何非故障進程接收到該消息,則所有非故障進程都會接收到。只要目標進程進行無限次嘗試接收,每條消息最終都會被傳遞,但是消息可能會被延遲任意長時間,并且可能按照任意順序進行傳遞。
問題模型:進程是傳遞消息的自動機,通過消息進行通信。
消息收發—> 狀態集計算----->消息收發
當前使用的異步提交協議似乎都存在“漏洞窗口”,即在算法執行期間的一段時間內,單個進程的延遲或不可訪問性可能導致整個算法無限等待。根據我們的不可能性結論,每個提交協議都有這樣的“窗口”,證實了民間智慧中廣泛認為的原理。
證明了漏洞窗口的存在
二、共識協議
一致性協議P是一個具有N個進程(N大于等于2)的異步系統。每個進程p都有一個一位輸入寄存器 x p x_p xp?,一個取值為(b, 0, 1)的輸出寄存器 y p y_p yp?,以及無限量的內部存儲空間。輸入和輸出寄存器的取值,加上程序計數器和內部存儲,構成了內部狀態。初始狀態規定了除了輸入寄存器之外的所有起始值;特別地,輸出寄存器的初始值為b。**輸出寄存器取值為0或1的狀態被認為是決策狀態。**進程p根據一個過渡函數進行確定性操作。一旦進程到達決策狀態,過渡函數就不能改變輸出寄存器的值;也就是說,輸出寄存器是“只寫”的。整個系統P由與每個進程對應的過渡函數和輸入寄存器的初始值來規定。
基本模型:
- 進程建模:系統由數量N>2的進程構成。進程被建模為狀態機,進行的動作即為由消息驅動的計算,通過對消息的收發進行的計算推動狀態機的狀態變化。每個進程具有一定的內部狀態。內部狀態包括輸入、輸出寄存器的取值,和程序計數器以及內部存儲值。進程還有
輸入寄存器:收消息的buffer
輸出寄存器:輸出最后的結果
內部狀態:輸入、輸出和寄存器的取值、程序計數器和內部存儲
- 初始狀態:規定了除了輸入寄存器外的所有值
- 輸出寄存器:b。當其取值為0或者1時的狀態被認為是決策狀態。
- 過渡函數:執行確定性操作。
進程通過發送消息來進行通信。消息是一個二元組 ( p , m ) (p, m) (p,m),其中p是目標進程的名稱,m是來自固定宇宙M的“消息值”。消息系統維護一個多重集合,稱為消息緩沖區,其中包含已發送但尚未傳遞的消息。它支持兩種抽象操作:
send(p,m):把消息 ( p , m ) (p,m) (p,m)放到消息緩沖區receive(p):從緩沖區刪除消息 ( p , m ) (p,m) (p,m)并且返回 m m m。在這種情況下,我們說 ( p , m ) (p,m) (p,m)被傳送(delivered),或者返回特殊的空值并保持緩沖區不變
因此,消息系統以非確定性方式運作,只有一個條件:如果receive(p)無限次執行,則消息緩沖區中的每個消息 ( p , m ) (p, m) (p,m)最終都會被傳遞。特別是,盡管緩沖區中存在消息 ( p , m ) (p, m) (p,m),消息系統仍可以有限次地返回0作為對receive(p)的響應。
系統的配置(configuration)由每個進程的內部狀態以及消息緩沖區的內容組成。初始配置是指每個進程都處于初始狀態,并且消息緩沖區為空。
配置 1 ? ? ? 收發消息與計算(步驟) ? ? ? > 配置 2 配置1---收發消息與計算(步驟)--->配置2 配置1???收發消息與計算(步驟)???>配置2
注意,系統的配置指的是系統中所有的進程的內部狀態以及消息緩沖區。與進程自身的自動機是不同的兩個概念。
一個步驟(step)將一個配置轉換到另一個配置,且僅由單個進程 p p p的基本步驟組成。記 C C C為一個配置。一個步驟分兩階段執行。首先,在 C C C的消息緩沖區上執行 receive ( p ) \text{receive}(p) receive(p),獲取值 m ∈ M ∪ ? m \in M \cup {\emptyset} m∈M∪?。之后,取決于 C C C中進程 p p p的內部狀態和消息 m m m, p p p轉換到新的內部狀態,并向其它進程發送有限數量的一組消息。由于進程是確定性的,因此該步驟完全取決于消息 e = ( p , m ) e=(p, m) e=(p,m),我們稱之為事件(event,此“事件”應認為是“ p p p收到 m m m”)。 e ( C ) e(C) e(C)表示產生的新配置,我們說 e e e可以應用到 C C C。注意事件 ( p , ? ) (p, \emptyset) (p,?)總是可以應用于 C C C,所以進程總是可以執行一個步驟。
步驟的概念
步驟包括兩個基本步驟:
receive(p)的執行,獲取消息- 根據消息和內部狀態轉換到新的內部狀態,并向其他進程發送數量有限的一組消息
事件的定義:事件e由消息(p, m)即來自某個進程的消息m,目標進程是p
從 C C C開始的一個調度(schedule),是一個有限或無限的事件序列 σ \sigma σ,它們從 C C C開始,依次應用。相關的步驟序列稱為一次執行(run)。若 σ \sigma σ是有限的,我們令 σ ( C ) \sigma(C) σ(C)表示產生的新配置,稱它可以從 C C C到達(reachable)。從某個初始配置可到達的配置稱為可達的(accessible)。下文涉及的所有配置都假設是可達的。
調度的概念:
- 調度是若干事件的序列(事件是作用于p的消息)
執行的概念:
- 步驟序列稱為一次執行
可達:
- 從某個初始配置可到達的配置稱為可達的
以下引理表明調度的“交換性”(commutativity)。
引理 1:假設從某配置 C C C開始,調度 σ 1 \sigma_1 σ1?, σ 2 \sigma_2 σ2?,分別產生配置 C 1 C_1 C1?, C 2 C_2 C2?。如果 σ 1 \sigma_1 σ1?與 σ 2 \sigma_2 σ2?中的進程集彼此不相交,那么 σ 2 \sigma_2 σ2?可以應用于 C 1 C_1 C1?,且 σ 1 \sigma_1 σ1?可以應用于 C 2 C_2 C2?,并且都產生相同的配置 C 3 C_3 C3?(見圖 1)。
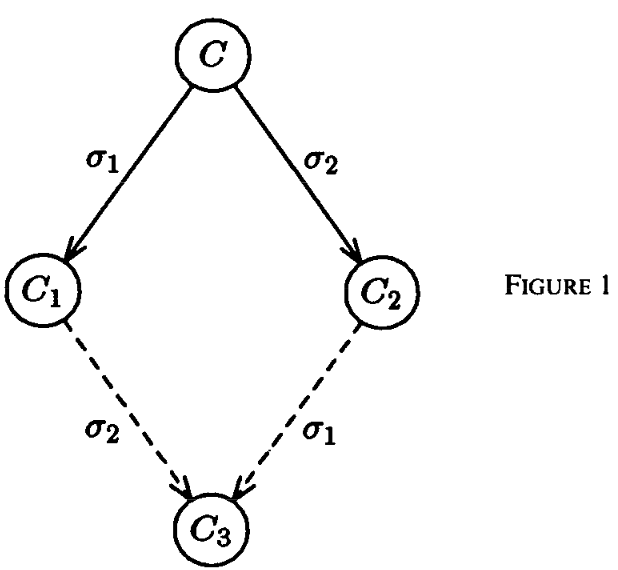
證明:因為 σ 1 \sigma_1 σ1?與 σ 2 \sigma_2 σ2?沒有關聯,由系統定義可以直接得出結論。
如果某個進程 p p p處于決定狀態,且 y p = v y_p=v yp?=v,那么我們說該配置 C C C的決定值為 v v v。若共識協議滿足下面兩個條件,則它是部分正確的(partially correct):
- 所有可達配置的決定值不超過一個。
- 某個可達配置的決定值為 v v v,且 v ∈ { 0 , 1 } v \in \set{0, 1} v∈{0,1}。
若在某次執行中,進程 p p p可以執行任意多的步驟,就稱為無故障的(non-faulty),否則是有故障的(faulty)。如果至多有一個進程有故障,且發送給無故障進程的消息最終都被收到,那么稱這一執行是可接受的(admissible)。
系統有無故障的定義
系統可接受的定義
若某個進程在執行中達到決定狀態,就稱此次執行是有決定的(deciding)。如果共識協議 P P P是部分正確的,且每個可接受的執行都是有決定的,那么稱其在一個進程故障的情況下仍完全正確(totally correct in spite of one fault)。我們的主定理表明,共識問題的所有部分正確協議都存在可接受但沒有決定的執行。
有決定的:進程在執行中達到決定狀態
完全正確:共識協議P是部分正確的,且每個可接受的執行都是有決定的。
三、主要結論
定理1:沒有共識協議在一個進程故障情況下仍完全正確(No consensus protocol is totally correct in spite of one fault)。
反證。假設共識協議 P P P在一個進程故障的情況下仍完全正確。我們來證明一系列引理,最終導致矛盾。
基本想法是展示協議永遠無法決斷的情況。這包括兩個步驟。首先,我們表明存在某個初始配置,不能預先確定決定值。其次,我們構造一個可接受的執行,總是避免系統執行做出決定的步驟。
令 C C C為一個配置, V V V是從 C C C可到達配置的決定值的集合。若 ∣ V ∣ = 2 |V|=2 ∣V∣=2,稱 C C C是雙值的(bivalent)。若 ∣ V ∣ = 1 |V|=1 ∣V∣=1,稱 C C C是單值的(univalent),根據相應的決定值,分別稱為“值-0”(0-valent)或“值-1”(1-valent)。由于 P P P是完全正確的,以及總有可接受的執行的事實, V ≠ ? V \ne \emptyset V=? 譯注:從而 ∣ V ∣ ≠ 0 |V| \ne 0 ∣V∣=0。
引理 2: P P P存在雙值的初始配置。
證明:假設不存在。因為假設 P P P是部分正確的,所以 P P P必定同時具有“值-0”和“值-1”的初始配置譯注:這兩類初始配置都是單值的。對兩個初始配置,如果它們僅有一個進程 p p p的初始值 x p x_p xp?不同,那么稱這兩個配置是毗連的(adjacent)。任意兩個初始配置都可以通過一系列毗連的初始配置聯系起來。因此,必然存在一個“值-0”的初始配置 C 0 C_0 C0?與一個“值-1”的初始配置 C 1 C_1 C1?毗連。令 p p p為它們之中初始值不同的那個進程。
現在考慮從 C 0 C_0 C0?開始的某個可接受且有決定的執行,其中進程 p p p不執行任何步驟,令 σ \sigma σ是該執行的調度。那么 σ \sigma σ也可以應用于 C 1 C_1 C1?,而且除了進程 p p p的內部狀態外,兩次執行對應的配置是相同的。易見,兩次執行最終會決定相同的值。若決定的值為1,則 C 0 C_0 C0?是雙值的;否則, C 1 C_1 C1?是雙值的。這兩種情況都與假定不存在雙值的初始配置相矛盾。
引理 3:令 C C C是 P P P中一個雙值配置, e = ( p , m ) e=(p,m) e=(p,m)是一個可應用于 C C C的事件。令 C \mathscr{C} C是從 C C C無需應用 e e e即可到達配置的集合, D = e ( C ) = { e ( E ) ∣ E ∈ C \mathscr{D} = e(\mathscr{C}) = \{e(E) | E \in \mathscr{C} D=e(C)={e(E)∣E∈C 且 e e e可以應用于 C } \mathscr{C}\} C}。那么, D \mathscr{D} D包含雙值的配置。
證明:既然 e e e可以應用于 C C C,那么由 C \mathscr{C} C的定義,及消息可以任意延遲的事實, e e e可以應用于每個 E ∈ C E \in \mathscr{C} E∈C。
假設 D \mathscr{D} D不包含雙值配置,那么其中的每個配置 D ∈ D D \in \mathscr{D} D∈D都是單值的。我們來推導出矛盾。
令 E i E_i Ei?是“值- i i i”的配置,可以從 C C C到達, i = 0 , 1 i=0, 1 i=0,1(因為 C C C是雙值的,故 E i E_i Ei?存在)。若 E i ∈ C E_i \in \mathscr{C} Ei?∈C,令 F i = e ( E i ) ∈ D F_i = e(E_i) \in \mathscr{D} Fi?=e(Ei?)∈D。否則,在到達 E i E_i Ei?的執行中就應用過了 e e e,故存在 F i ∈ D F_i \in \mathscr{D} Fi?∈D,且從 F i F_i Fi?可到達 E i E_i Ei?。在任一情況下, F i F_i Fi?都是“值- i i i”的,由于 F i F_i Fi?不是雙值的(因為 F i ∈ D F_i \in \mathscr{D} Fi?∈D,而 D \mathscr{D} D不包含雙值配置)且 E i E_i Ei?可到達 F i F_i Fi?或反之。由于 F i ∈ D F_i \in \mathscr{D} Fi?∈D, i = 0 , 1 i = 0, 1 i=0,1, D \mathscr{D} D同時包含“值-0”和“值-1”的配置。
若一個配置經一步到達另一個配置,則稱這兩個配置是鄰居(neighbors)。通過簡單的歸納,存在鄰居 C 0 , C 1 ∈ C C_0,\ C_1 \in \mathscr{C} C0?,?C1?∈C,且 D i = e ( C i ) D_i = e(C_i) Di?=e(Ci?)是“值- i i i”的, i = 0 , 1 i = 0, 1 i=0,1。不失一般性,令 C 1 = e ′ ( C 0 ) C_1 = e'(C_0) C1?=e′(C0?),其中 e ′ = ( p ′ , m ′ ) e'=(p',m') e′=(p′,m′)。
情況1:若 p ′ ≠ p p' \ne p p′=p,由引理1,得 D 1 = e ′ ( D 0 ) D_1 = e'(D_0) D1?=e′(D0?)?。這是不可能的,因為“值-0”配置的任何后繼都是“值-0”的(見圖 2)。
情況2:若 p ′ = p p' = p p′=p,考慮從 C 0 C_0 C0?的任意有限步有決定的執行,其中 p p p不執行任何步驟。
令 σ \sigma σ是相應的調度, A = σ ( C 0 ) A = \sigma(C_0) A=σ(C0?)。由引理 1, σ \sigma σ可應用于 D i D_i Di?,并產生“值- i i i”的配置 E i = σ ( D i ) E_i = \sigma(D_i) Ei?=σ(Di?), i = 0 , 1 i = 0, 1 i=0,1。同樣由引理 1, e ( A ) = E 0 e(A) = E_0 e(A)=E0?,且 e ( e ′ ( A ) ) = E 1 e(e'(A)) = E_1 e(e′(A))=E1?(見圖 3)。因此, A A A是雙值的。但這是不可能的,因為到 A A A的執行是有決定的(由假設),所以 A A A必須是單值的。
在每種情況下,我們都遇到了矛盾,所以 D \mathscr{D} D包含雙值的配置。






)












