1 Abstract
- 這篇論文研究了與非凸函數g相關的廣義奇異值閾值(Generalized Singular Value Thresholding, GSVT)算子Proxσ g (·),定義為 P r o x g σ ( B ) = arg ? min ? X ∑ i = 1 m g ( σ i ( X ) ) + 1 2 ∥ X ? B ∥ F 2 , \mathbf{Prox}_{g}^{\sigma}(\mathbf{B})=\arg\min_{ \mathbf{X}} \sum_{i=1}^{m}g(\sigma_{i}(\mathbf{X}))+\frac{1}{2}\|\mathbf{X}-\mathbf{B}\|_{F}^{2}, Proxgσ?(B)=argminX?∑i=1m?g(σi?(X))+21?∥X?B∥F2?,,其中X的奇異值為σi(X)。作者證明了當g是下界有界時,可以通過對奇異值執行g的近端算子(Proxg(·))來獲得GSVT,因為Proxg(·)是單調的。如果非凸g滿足某些條件(許多流行的非凸替代函數,例如?p-范數,0 < p < 1,是?0-范數的特例),作者為任何b ≥ 0提出了一個通用的求解Proxg(b)的方法。GSVT極大地推廣了已知的奇異值閾值(Singular Value Thresholding, SVT),后者是許多凸低秩最小化方法中的基本子程序。通過使用GSVT代替SVT,作者能夠解決非凸低秩最小化問題。
引言部分提到,稀疏和低秩結構近年來受到了廣泛關注。許多應用利用這兩種結構,例如面部識別(Wright等人,2009年)、子空間聚類(Cheng等人,2010年;Liu等人,2013b)和背景建模(Candès等人,2011年)。為了實現稀疏性,一個原則性方法是使用凸?1-范數。然而,?1-最小化可能是次優的,因為?1-范數是?0-范數的一個寬松近似,經常導致過度懲罰的問題。這使得人們的注意力回到了通過插值?0-范數和?1-范數之間的非凸替代方法上。已經提出了許多非凸懲罰項,包括?p-范數(0 < p < 1)(Frank和Friedman,1993年)、平滑剪裁絕對偏差(Smoothly Clipped Absolute Deviation, SCAD)(Fan和Li,2001年)、對數(Logarithm)(Friedman,2012年)、最小極大凹懲罰(Minimax Concave Penalty, MCP)(Zhang等人,2010年)、Geman(Geman和Yang,1995年)和拉普拉斯(Laplace)(Trzasko和Manduca,2009年)。它們的定義在表1中展示。數值研究(Candès、Wakin和Boyd,2008年)表明,非凸優化通常優于凸模型。
2 Algorithm
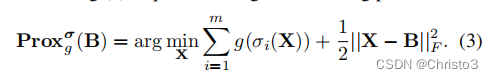
3 Optimization Strategy



3 Performance

4 Advantages and Disadvantages
在提供的文檔中,廣義奇異值閾值(GSVT)方法的優缺點可以從以下幾個方面進行總結:
優點:
-
泛化能力:GSVT方法能夠泛化已知的奇異值閾值(SVT)方法,使其適用于非凸優化問題,這在處理低秩矩陣恢復和稀疏信號恢復等問題時非常有用。
-
理論證明:文檔中提供了GSVT算子的數學證明,證明了對于任何下界有界的非凸函數g,其近端算子Proxg(·)是單調的,這為算法的穩定性和可靠性提供了理論基礎。
-
算法效率:GSVT方法通過固定點迭代算法來求解問題,這在實踐中可能非常快速,尤其是當只需要在[0, b]的區間內搜索時。
-
通用性:GSVT方法不僅適用于特定的非凸函數,而且為一大類滿足特定條件的非凸函數提供了解決方案。
視覺與控制前沿公眾號,第一時間獲取最有價值的前沿視覺與控制文章。



















)
