????????在計算機科學中，樹是一種抽象數據類型（ADT）或是實現這種抽象數據類型的數據結構，用來模擬具有樹狀結構性質的數據集合。這種數據結構以一系列連接的節點來形成樹形結構。在C++中，樹的概念和存儲結構是實現各種復雜算法和數據操作的基礎。???

?????樹是由節點和邊組成的圖，其中每個節點有零個或多個子節點，但只有一個父節點（除了根節點，它沒有父節點）。樹的頂部節點稱為根節點。如果一個節點沒有子節點，那么它被稱為葉子節點。除了根節點和葉子節點之外的其他節點稱為內部節點。由樹的根節點和若干棵子樹所構成的樹稱為森林。如下圖所示。

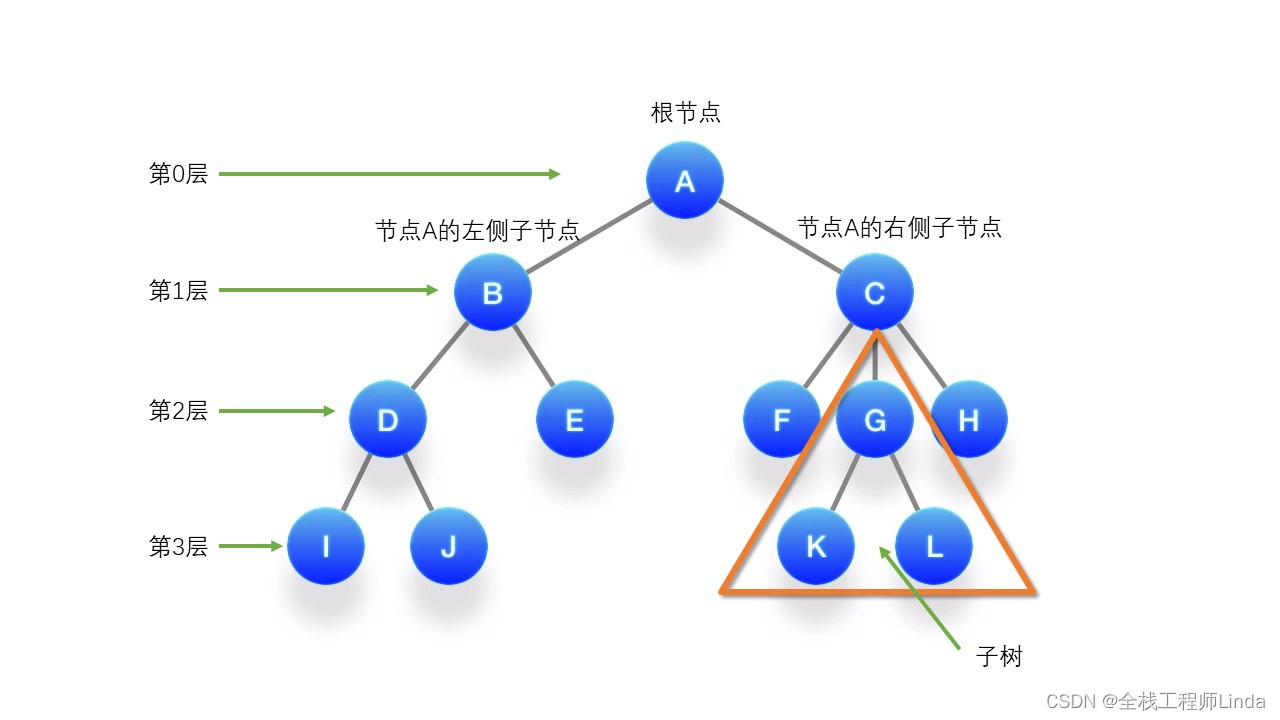
?????????樹的術語：? ??

????????（1）路徑：在兩個節點之間，一系列的邊和節點的組合。路徑的長度是組成路徑的邊數。

????????（2）深度：一個節點的深度是指從根節點到該節點的最長路徑上的邊數。根節點的深度為0。

????????（3）層次：樹的層次從根開始定義，根為第一層，根的子節點為第二層，以此類推。

????????（4）高度：樹的高度是從葉子節點開始自底向上逐層累加的路徑上邊的數量。根節點的高度就是樹的高度。

????????在C++中，樹的存儲結構主要有兩種：順序存儲和鏈式存儲。不同的存儲結構對應著不同的表示方法，如孩子表示法、雙親表示法、孩子兄弟表示法等。

????????1. 順序存儲：順序存儲通常用于完全二叉樹。在完全二叉樹中，除了最后一層外，其他層的節點數是滿的，并且最后一層的節點都靠左排列。這種特性使得完全二叉樹可以使用數組進行順序存儲，其中每個節點的索引與其在樹中的位置相關。

? ? ? ? 示例：創建一棵簡單的完全二叉樹，代碼如下。

#include <iostream>
#include <vector>using namespace std;class TreeNode {
public:int value;TreeNode* left;TreeNode* right;TreeNode(int x) : value(x), left(nullptr), right(nullptr) {}
};class BinaryTree {
private:vector<TreeNode*> nodes;
public:// 初始化樹的根節點void initRoot(int value) {nodes.push_back(new TreeNode(value));}// 添加子節點void addChild(int parentIndex, int leftChildValue, int rightChildValue) {int nextEmptyIndex = nodes.size();if (leftChildValue != -1) {nodes.push_back(new TreeNode(leftChildValue));nodes[parentIndex]->left = nodes[nextEmptyIndex];}if (rightChildValue != -1) {nodes.push_back(new TreeNode(rightChildValue));nodes[parentIndex]->right = nodes[nextEmptyIndex + (leftChildValue != -1)];}}// 示例：創建一棵簡單的完全二叉樹void createExampleTree() {initRoot(1);addChild(0, 2, 3);addChild(1, 4, 5);addChild(2, 6, -1);addChild(3, 7, 8);}// 其他操作，如遍歷、查找等...
};

????????鏈式存儲：鏈式存儲通過節點和指針來表示樹中的關系。每個節點包含數據域和指向其子節點的指針域。鏈式存儲方式更加靈活，適用于各種類型的樹。

? ? ? ? 示例一：使用孩子表示法創建樹，代碼如下。

class TreeNode {
public:int value;vector<TreeNode*> children;TreeNode(int x) : value(x) {}
};// 使用孩子表示法創建樹
TreeNode* createTree() {TreeNode* root = new TreeNode(1);TreeNode* node2 = new TreeNode(2);TreeNode* node3 = new TreeNode(3);TreeNode* node4 = new TreeNode(4);TreeNode* node5 = new TreeNode(5);root->children.push_back(node2);root->children.push_back(node3);node2->children.push_back(node4);node2->children.push_back(node5);return root;
}

????????上述代碼展示了如何使用孩子表示法來創建一個樹，其中每個節點都有一個指向其子節點的指針列表。這種方式可以很直觀地表示一個節點的所有子節點，但是在查找父節點時不夠高效，因為父節點的信息并未存儲在當前節點中。

????????在雙親表示法中，每個節點不僅包含數據域和指向其子節點的指針，還包含一個指向其父節點的指針。這使得我們可以方便地訪問一個節點的父節點，但可能需要額外的空間來存儲父節點的指針。

? ? ? ? 示例二：使用雙親表示法創建樹，代碼如下：

class TreeNode {
public:int value;TreeNode* parent; // 指向父節點的指針vector<TreeNode*> children; // 子節點列表TreeNode(int x) : value(x), parent(nullptr) {}
};// 使用雙親表示法創建樹
void createTreeWithParent(TreeNode*& root) {root = new TreeNode(1); // 根節點的父節點為nullTreeNode* node2 = new TreeNode(2);TreeNode* node3 = new TreeNode(3);TreeNode* node4 = new TreeNode(4);TreeNode* node5 = new TreeNode(5);node2->parent = root;node3->parent = root;node4->parent = node2;node5->parent = node2;root->children.push_back(node2);root->children.push_back(node3);node2->children.push_back(node4);node2->children.push_back(node5);
}

????????在雙親表示法中，我們可以沿著父節點的指針向上遍歷樹，直到找到根節點或者到達一個父節點為空的節點。這種表示法在需要頻繁進行父子節點關系查詢時比較有用。

????????孩子兄弟表示法是一種結合了孩子表示法和雙親表示法的思想的方法。在這種表示法中，每個節點包含指向其第一個孩子節點的指針和指向其下一個兄弟節點的指針。這種表示法對于二叉樹非常自然，并且可以很方便地表示任何類型的樹。
? ? ? ? 示例三：?使用孩子兄弟表示法創建樹，代碼如下：

class TreeNode {
public:int value;TreeNode* firstChild; // 指向第一個孩子節點TreeNode* nextSibling; // 指向下一個兄弟節點TreeNode(int x) : value(x), firstChild(nullptr), nextSibling(nullptr) {}
};// 使用孩子兄弟表示法創建樹
void createTreeWithChildSibling(TreeNode*& root) {root = new TreeNode(1);TreeNode* node2 = new TreeNode(2);TreeNode* node3 = new TreeNode(3);TreeNode* node4 = new TreeNode(4);TreeNode* node5 = new TreeNode(5);root->firstChild = node2;node2->nextSibling = node3;node3->firstChild = node4;node3->nextSibling = node5;
}

????????在這種表示法中，通過firstChild可以訪問到該節點的所有子節點，而通過nextSibling可以遍歷該節點的所有兄弟節點。這種方法特別適合處理那些子節點之間沒有順序要求的樹結構。

????????每種存儲結構都有其適用的場景和優缺點，例如順序存儲適合表示完全二叉樹，而鏈式存儲則更加靈活，能夠表示任意結構的樹。在實際應用中，需要根據具體需求和樹的特點來選擇適當的存儲結構。