有一位國王擁有5座金礦，每座金礦的黃金儲量不同，需要參與挖掘的工人人數也不同。

例如，有的金礦儲量是5ookg黃金，需要5個工人來挖掘;有的金礦儲量是2ookg黃金，需要3個工人來挖掘...... 如果參與挖礦的工人的總數是10。每座金礦要么全挖，要么不挖，不能派出一半人挖取一半的金礦。要求用程序要想得到盡可能多的黃金，應該選擇挖取哪幾座金礦?

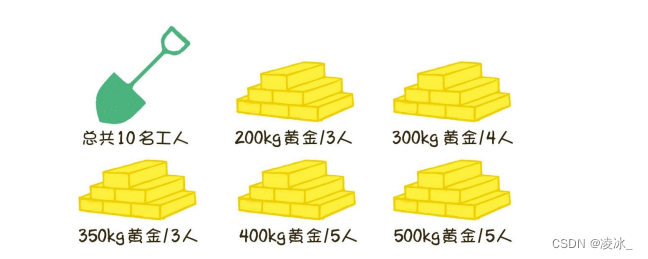
金礦按照性價比從高到低進行排序，排名結果如下:

第1名，350kg黃金/3人的金礦，人均產量約為116.6kg黃金。

第2名，500kg黃金/5人的金礦，人均產量為100kg黃金。

第3名，400kg黃金/5人的金礦，人均產量為80kg黃金。

第4名，300kg黃金/4人的金礦，人均產量為75kg黃金。

第5名，200kg黃金/3人的金礦，人均產量約為66.6kg黃金。

由于工人數量是10人，優先挖掘性價比排名為第1名和第2名的金礦之后，工人還剩下2人，不夠再挖掘其他金礦了。

得出的最佳金礦收益是350+500即850kg黃金。
解決思路是使用貪心算法。這種思路在局部情況下是最優解，但是在整體上卻未必是最優的。

? ? 如果我放棄性價比最高的350kg黃金/3人的金礦，選擇500kg黃 金/5人和400kg黃金/5人的金礦，加起來收益是900kg黃金，是不是大于你得到的850kg黃金?

動態規劃，就是把復雜的問題簡化成規模較小的子問題，再從簡單的子問題自底向上一步一步遞推，最終得到復雜問題的最優解。?

10個工人在前4個金礦的收益，和7個工人在前4個金礦的收益+最后一個金礦的收益誰大誰小了。

?首先針對10個工人4個金礦這個子結構，第4個金礦（300kg黃金/4人）可以選擇挖與不挖。根據第4個金礦的選擇，問題又簡化成了兩種更小的子結構:

1、10個工人在前3個金礦中做出最優選擇。

2、(10-4=6）6個工人在前3個金礦中做出最優選擇。

相應地，對于7個工人4個金礦這個子結構，第4個金礦同樣可以選擇挖與不挖。根據第4個金礦的選擇，問題也簡化成了兩種更小的子結構:

1、7個工人在前3個金礦中做出最優選擇。

2、(7-4=3）3個工人在前3個金礦中做出最優選擇。

就這樣，問題一分為二，二分為四，一直把問題簡化成在0個金礦或0個工人時的最優選擇，這個收益結果顯然是0，也就是問題的邊界。
這就是動態規劃的要點:確定全局最優解和最優子結構之間的關系，以及問題的邊界。

這個關系用數學公式來表達，叫作狀態轉移方程式。

金礦數量設為n，工人數量設為w，金礦的含金量設為數組g[]，金礦所需開采人數設為數組p[]，設F (n，w）為n個金礦、w個工人時的最優收益函數，那么狀態轉移方程式如下:

F(n，w) =0 (n=0或w=0)? ? ?問題邊界，金礦數為0或工人數為0的情況。

F(n,w)=F(n-1,w)(n≥1,w<p[n-1])? ? 當所剩工人不夠挖掘當前金礦時，只有一種最優子結構。

F(n,w)= max(F(n-1,w),F(n-1,w-p[n-1])+g[n-1])(n≥1,wzp[n-1])? ? 在常規情況下，具有兩種最優子結構（挖當前金礦或不挖當前金礦）。?

?

在上圖中，標為橘色的方法調用是重復的。可以看到F (2，7) 、F(1，7)、F (1，2)這幾個入參相同的方法都被調用了兩次。

當金礦數量為5時，重復調用的問題還不太明顯。金礦數量越多，遞歸層次越深，重復調用也就越多，這些無謂的調用必然會降低程序的性能。?

動態規劃的另一個核心要點:自底向上求解。

此時，最后1行最后1個格子所填的900就是最終要求的結果，即5個金礦、10個工人的最優收益是9ookg黃金。?

使用二維數組來代表表格

def get_best_gold(worker,person=[],gold=[]):''':param worker:  工人數量:param person:  金礦開采人數:param gold:  金礦存儲量:return:  最優收益'''#初始化表格0r_table=[[0 for i in range(worker+1)] for j in range(len(gold)+1)]double_for(r_table)print('&'*50)#填充表格數據for i in range(1,len(gold)+1):for j in range(1,worker+1):if j<person[i-1]:r_table[i][j]=r_table[i-1][j]else:r_table[i][j] =max(r_table[i - 1][j],r_table[i - 1][j-person[i-1]]+gold[i-1])double_for(r_table)#返回最后一個格子的數據return r_table[len(gold)][worker]def double_for(ll):for row in ll:print(row)if __name__ == '__main__':#采礦人數person=[5,5,3,4,3]#采礦黃金量gold=[400,500,200,300,350]print(get_best_gold(10, person, gold))

? ? ? 程序利用雙循環來填充一個二維數組，所以時間復雜度和空間復雜度都是O ( nw) ，比遞歸的性能好多啦!?

def get_best_gold2(worker,person=[],gold=[]):'''優化:param worker:  工人數量:param person:  金礦開采人數:param gold:  金礦存儲量:return:  最優收益'''#初始化表格0results=[0]*(worker+1)print(results)#填充一維數據for i in range(1,len(gold)+1):for j in range(worker,0,-1):if j>=person[i-1]:results[j] =max(results[j],results[j-person[i-1]]+gold[i-1])print(results)#返回最后一個格子的數據return results[worker]if __name__ == '__main__':#采礦人數person=[5,5,3,4,3]#采礦黃金量gold=[400,500,200,300,350]print(get_best_gold2(10, person, gold))

空間復雜度降低到了O (n)。?