計數排序，基數排序，桶排序

計數排序:

基數排序：

桶排序:

計數排序:

計數排序是一種非比較型整數排序算法，特別適用于一定范圍內的整數排序。它的核心思想是使用一個額外的數組（稱為計數數組）來計算每個值的出現次數，然后根據這些計數信息將所有的數字放到正確的位置上，從而實現排序。

大致流程就是這樣的，我會用圖和代碼的思想給大家講清楚的：

確定范圍：首先遍歷一遍待排序的數組，找出其中最大值和最小值，從而確定數字的范圍。這是因為計數排序要求輸入數據在一個已知的有限范圍內。
初始化計數數組：創建一個長度為最大值與最小值之差加一的計數數組，并將所有元素初始化為0。計數數組的索引代表原始數組中的數值，值則表示該數值出現的次數。
計數：再次遍歷原始數組，對于每個元素，將計數數組中對應索引的值加一，即統計每個元素出現的次數。
累加計數：對計數數組進行累加操作，使得計數數組中的每個元素變成小于等于其索引值的所有元素的累計總和。這樣，計數數組中的每個位置就表示了在排序后數組中相應數值的起始位置。
重建數組：最后，從計數數組反向遍歷原始數組，根據計數數組的信息將元素放到排序后數組的正確位置上。當把一個元素放到排序后數組時，相應地減少計數數組中該元素的計數，以保持計數的準確性。

第一步：創建一個數組，并且找到其中的最大值和最小值

第二步：定義一個count數組(最大值減去最小值加一)，用來統計每個數字出現的次數

?第三步：遍歷count數組，然后按照大小順序把依次放回array數組里面去(可以理解成覆蓋了原數組)，最后出來的結果就可以按照大小順序看到每一個數字出現的多少次

最后出來的結果就是：[1, 1, 2, 3, 4, 5, 5, 6, 8, 9, 9]

public static int[] countSort(int[] array){int minval = array[0];int maxval = array[0];for(int i = 0;i<array.length;i++){if(array[i] < minval){minval = array[i];}if(array[i] > maxval){maxval = array[i];}}int[] count = new int[maxval-minval+1];for(int i = 0;i<array.length;i++){int val = array[i];count[val-minval]++;}//遍歷計數數組int index = 0;for(int i = 0;i<count.length;i++){while(count[i]>0){array[index] = i+minval;index++;count[i]--;}}return array;}

時間復雜度:

計數排序的時間復雜度主要由兩部分組成：統計每個元素出現次數和根據統計結果重構輸出數組。對于n個元素，范圍在0到k之間的整數排序，計數排序的時間復雜度為O(n+k)。其中，n是數組長度，k是數組中最大值與最小值的差加1。在最好的情況下（即k接近n或n），時間復雜度接近線性，但在k遠大于n時，時間復雜度會顯著增長。

空間復雜度:

計數排序需要額外的空間來存儲每個元素的計數，這個空間取決于待排序數組中元素的范圍。具體來說，需要一個大小為k+1的計數數組，其中k是數組中的最大值與最小值之差加1。因此，空間復雜度為O(k)。如果k與n同數量級，那么空間復雜度也是線性的，即O(n)。

穩定性:

計數排序是一種穩定的排序算法。因為它在統計每個元素的頻率之后，按照元素原來的順序（通過第二個循環從最小元素開始逐個累加計數數組并放回原數組）將元素放回原數組，保證了相同元素的相對位置不會改變。

基數排序：

它的核心思想是將待排序的元素根據其每一位的數值進行分配，這個過程通常從最低有效位（LSD）開始，也可以從最高有效位（MSD）開始，然后按位遞進，直到最高位。基數排序利用了分配式排序的策略，也被稱為“桶排序”的一種推廣。

第一步:首先得有一個數組然后才能對數組進行排序，找到數組中的最大值，確定最大值的位數，比如198就是3位數

第二步：新建一個buckets數組，根據個位十位百位...來存放數據

1.按照個位數排序就是這樣的，然后我們按照先進先出的原則拿出來

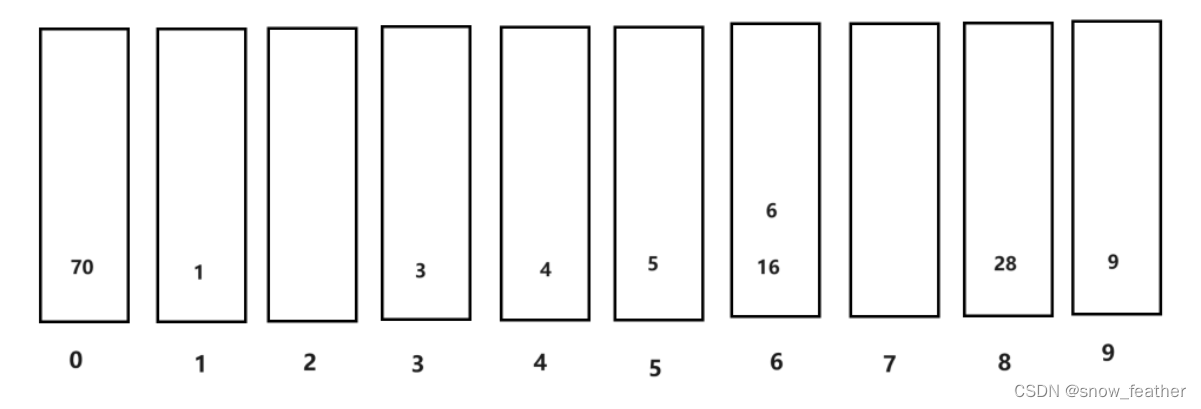2.此時的buckets數組就是：

3.因為最大為2位數，所以我們還得再進行一個十位的比較

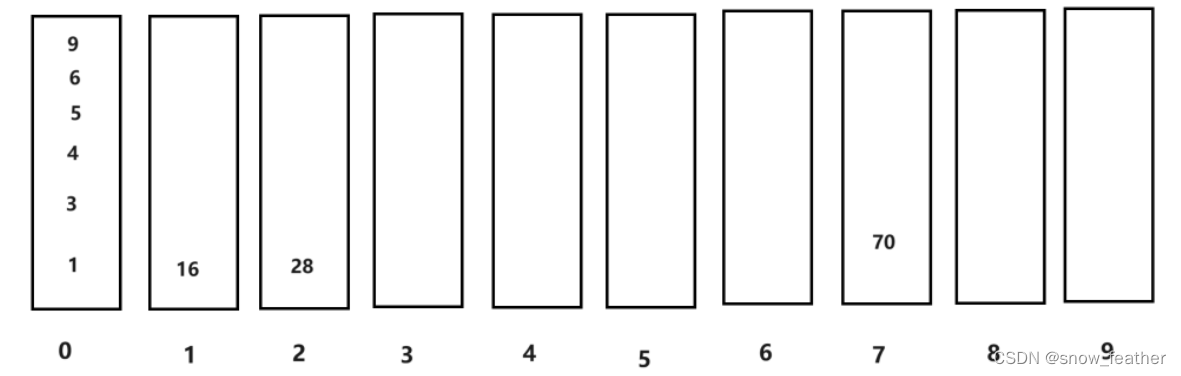
4.?按照先進先出的原則拿出來就得到最終結果：

private static int getMaxDigits(int[] array){int maxnum = array[0];for(int num : array){if(num > maxnum){maxnum = num;}}return (int)Math.log10(maxnum)+1;
}public static int[] radixSort(int[] array){int maxnum = getMaxDigits(array);int radix = 10;//基數是10 因為是10進制List<Integer>[] buckets = new ArrayList[radix];for(int i = 0;i < radix;i++){buckets[i] = new ArrayList<>();}for(int digit = 1;digit <= maxnum;digit++){//記得每次要把桶清空for (List<Integer> bucket : buckets) {bucket.clear();}for (int num : array) {int index = (num / (int)Math.pow(10,digit-1))%10;buckets[index].add(num);}//從桶中收集元素到數組int index = 0;for(List<Integer> bucket : buckets){for(int num : bucket){array[index] = num;index++;}}}return array;
}

時間復雜度:

基數排序的時間復雜度主要取決于數字的位數（d，即最大數的位數）和待排序元素的數量（n）。
最好、平均和最壞情況下，基數排序的時間復雜度都是O(d*(n+k))，其中k是基數（通常是10，因為基數排序常用于十進制數）。這意味著排序的總成本是元素數量乘以位數，加上每一輪分配和收集過程中桶的管理開銷。當d和k相對于n較小或固定時，基數排序非常高效。

空間復雜度:

空間復雜度主要來自于存儲桶（或列表）的需要。基數排序需要額外的空間來存放每個基數下的元素。最壞情況下，每個元素都會進入不同的桶中，因此空間復雜度為O(n+k)。但實際上，由于基數排序是分輪進行的，每輪只需要足夠的空間來存放每個桶中的元素，理想情況下空間復雜度可以近似為O(n)。但是，考慮到實際實現中可能會為每一輪都分配桶空間，總的空間復雜度還是O(n+k)。

穩定性:

基數排序是穩定的排序算法。這意味著相等的元素在排序前后相對位置保持不變。這是因為基數排序是按位進行的，每一趟排序都是獨立的，并且在收集階段按照原順序從桶中取出元素，從而保持了穩定性。

桶排序:

初始化桶：首先確定桶的數量和每個桶覆蓋的數值范圍。桶的數量和分布取決于待排序數據的特性，通常需要預先知道數據的大致分布情況。
分配元素到桶：遍歷待排序數組，根據元素的值將它們分配到對應的桶中。分配的依據可以是元素的大小，例如，如果數據范圍是0到100，可以創建10個桶，每個桶負責10個數的范圍。
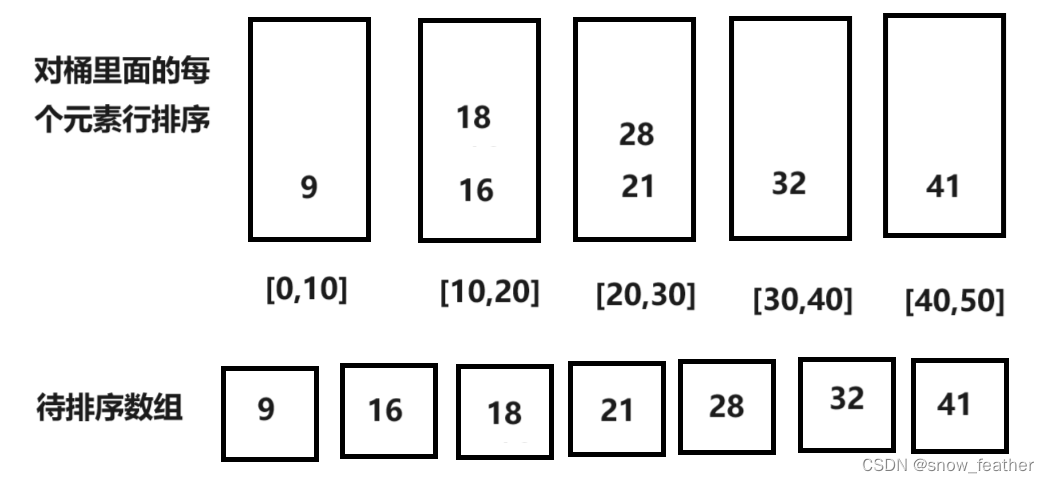
桶內排序：對每個非空的桶內部進行排序。可以選擇插入排序、快速排序等算法，具體選擇取決于桶內元素的數量和特性。
合并桶：將所有桶中的元素按照桶的順序（通常是桶的索引）依次取出，合并到一個數組中，這樣合并后的數組就是有序的。

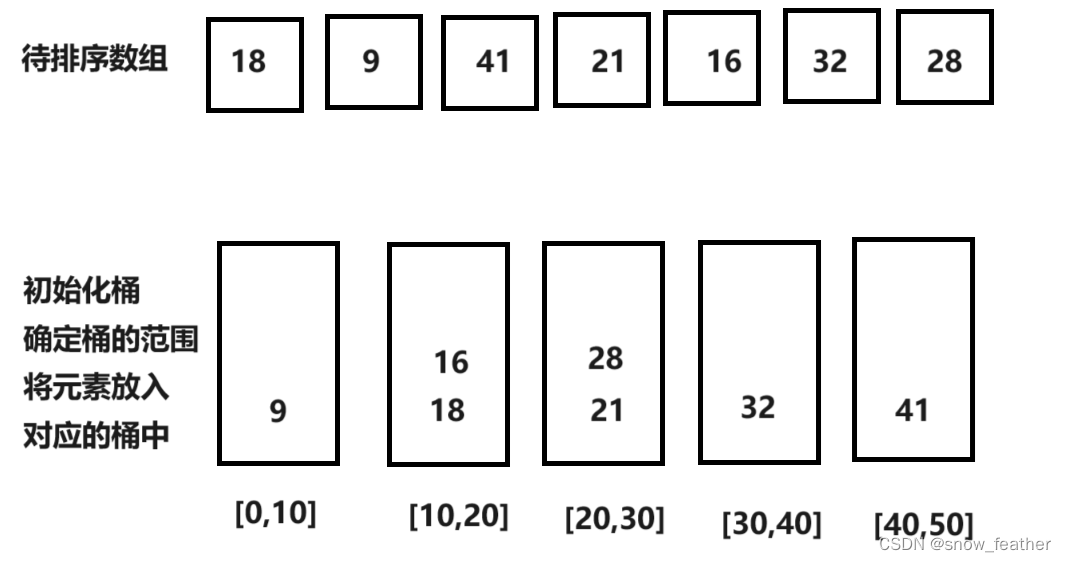
代碼實現：?

public static int[] bucketSort(int[] arr){int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int num : arr){max = Math.max(max,num);min = Math.min(min,num);}//初始化桶int bucketnum = (max-min)/arr.length+1;List<Integer>[] buckets = new ArrayList[bucketnum];for (int i = 0; i < bucketnum; i++) {buckets[i] = new ArrayList<>();}//將每個元素放入桶中for (int i = 0; i < arr.length; i++) {int index = (arr[i] - min) * (bucketnum - 1) / (max - min);buckets[index].add(arr[i]);}//對桶里面的每個元素進行排序，這里可以自己實現其他排序算法for (int i = 0; i < buckets.length; i++) {Collections.sort(buckets[i]);}//重新將桶中的每個元素放回到原數組中int index = 0;for (int i = 0; i < buckets.length; i++) {for(int j = 0;j<buckets[i].size();j++){arr[index] = buckets[i].get(j);index++;}}return arr;}

時間復雜度:

最好情況：如果數據均勻分布在各個桶中，且桶內排序所用的算法具有良好的時間復雜度（如插入排序在小數組上接近O(n)），桶排序的整體時間復雜度可以達到O(n + k)，其中n是待排序元素的數量，k是桶的數量。
平均情況：同樣，如果數據分布較為均勻，桶排序的時間復雜度也是O(n + k)。
最壞情況：如果所有數據都集中在少數幾個桶中，特別是全部集中在同一個桶里，此時桶排序的時間復雜度退化，需要對這些桶內的元素進行排序，可能會達到O(n^2)，這取決于桶內排序算法的時間復雜度。

空間復雜度: