198.打家劫舍

你是一個專業的小偷，計劃偷竊沿街的房屋。每間房內都藏有一定的現金，影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警。

給定一個代表每個房屋存放金額的非負整數數組，計算你?不觸動警報裝置的情況下?，一夜之內能夠偷竊到的最高金額。

解題思路：

確定dp數組含義：dp[i]遍歷到房屋index為i時所能打劫到的最多錢

確認遞推公式：dp[i]取決于前一個房屋和前兩個房屋是否有被偷，如果前一個被偷，則不能偷第i個，如果第i-2個被偷，可選擇是否偷第i個。dp[i] = max(dp[i-2]+nums[i], dp[i-1])

初始化：dp[0] = nums[0], dp[1] = max(nums[0], nums[1])

遍歷順序：從小到大遍歷

打印dp數組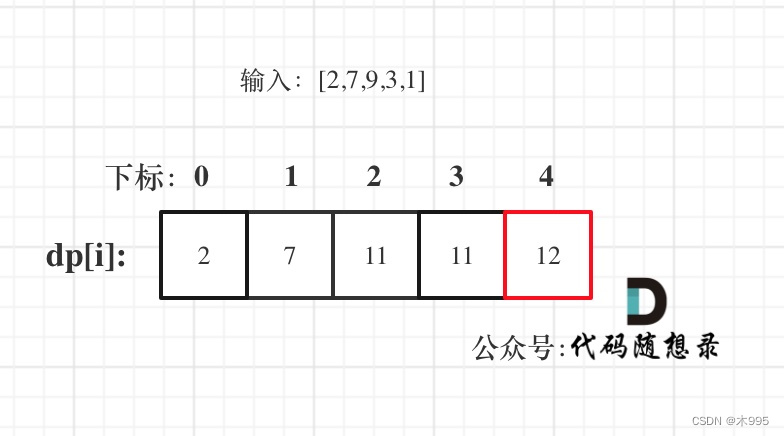

class Solution:def rob(self, nums: List[int]) -> int:if len(nums)<=1:return nums[0]dp = [0]*(len(nums))dp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, len(nums)):dp[i] = max(dp[i-2]+nums[i], dp[i-1])return dp[len(nums)-1]

class Solution:def rob(self, nums: List[int]) -> int:if len(nums)<=1:return nums[0]def helper(subnums):if len(subnums)<=1:return subnums[0]dp = [0]*len(subnums)dp[0] = subnums[0]dp[1] = max(subnums[0], subnums[1])for i in range(2, len(subnums)):dp[i] = max(dp[i-2]+subnums[i], dp[i-1])print(dp)return dp[len(subnums)-1]return max(helper(nums[:-1]), helper(nums[1:]))

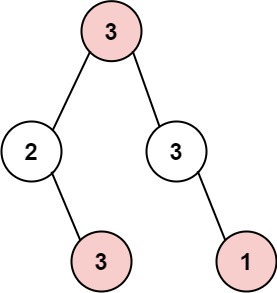
輸入: root = [3,2,3,null,3,null,1]
輸出: 7 
解釋:?小偷一晚能夠盜取的最高金額 3 + 3 + 1 = 7

解題思路：

本體使用遞歸三部曲結合dp五步驟，設置dp[0],dp[1]表示打劫當前節點和不打劫當前節點的最大值，每個node有一組對應的dp[0], dp[1]。使用后序遍歷，當前節點dp值需要結合其左右節點dp進行分析。?遞歸三步驟：確定遞歸參數，確定停止條件，遞歸邏輯。輸入參數統一為當前節點即表示為root， 當root == null停止并返回0，再遍歷左右子樹，中間值取最大dp值。

重點理解

val1 = root.val + leftdp[0] + rightdp[0]#行竊root

val2 = max(leftdp[0],leftdp[1])+max(rightdp[0], rightdp[1])#不行竊root，選取左右子樹行竊或不行竊時的最大值，兩邊取max。

代碼如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:def helper(root):if not root:return [0,0]leftdp = helper(root.left)rightdp = helper(root.right)val1 = root.val + leftdp[0] + rightdp[0]#行竊rootval2 = max(leftdp[0],leftdp[1])+max(rightdp[0], rightdp[1])#不行竊rootreturn [val2, val1]return max(helper(root))