姿態解算

一、主線

姿態表示方式：矩陣表示，軸角表示，歐拉角表示，四元數表示。

慣性測量單元IMU（Inertial Measurement Unit）：MPU6050芯片，包含陀螺儀和加速度計，分別測量三軸加速度和三軸角速度。注意，傳感器所測數據是原始數據，包含了噪聲，無法直接用于飛行器的姿態解算，因此需要對數據進行濾波。

濾波算法：非線性互補濾波算法，卡爾曼濾波算法，Mahony互補濾波算法。

二、知識點補充

加速度計和陀螺儀

加速度計：加速度計,可以測量加速度,包括外力加速度和重力加速度,因此，當被測物體在靜止或勻速運動（勻速直線運動）的時候,加速度計僅僅測量的是重力加速度,而重力加速度與 R 坐標系（絕對坐標系）是固連的,通過這種關系,可以得到加速度計所在平面與地面 的角度關系 也就是橫滾角和俯仰角。把加速度傳感器水平靜止放在桌子上，它的Z軸輸出的是1g的加速度。因為它Z軸方向被重力向下拉出了一個形變。可惜的是，加速度傳感器不會區分重力加速度與外力加速度。所以，當系統在三維空間做變速運動時，它的輸出就不正確了，或者說它的輸出不能表明物體的姿態和運動狀態。

陀螺儀：陀螺儀測量角速度。陀螺儀模型如圖所示，陀螺儀的每個通道檢測一個軸的旋轉。

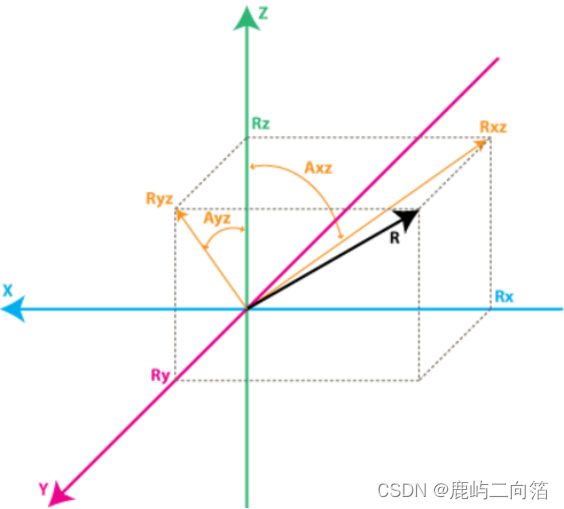
圖2[引自網絡]?

上圖中，Rxz是R在XZ面上的投影，與Z軸的夾角為Axz。Ryz是R在ZY面上的投影，與Z軸的夾角為Ayz。陀螺儀就是測量上面定義角度的變化率，換句話說，它會輸出一個與上面這些角度變化率線性相關的值。

加速度計工作原理介紹（摘自網絡）

大多數加速度計可歸為兩類：數字和模擬。數字加速度計可通過I2C，SPI或USART方式獲取信息，而模擬加速度計的輸出是一個在預定范圍內的電壓值，你需要用ADC（模擬量轉數字量）模塊將其轉換為數字值。不管使用什么類型的ADC模塊，都會得到一個在一定范圍內的數值。例如一個10位ADC模塊的輸出值范圍在0-1023間。假設我們從10位ADC模塊得到了以下的三個軸的數據：

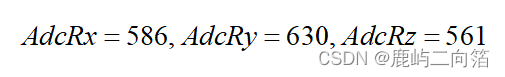
每個ADC模塊都有一個參考電壓，假設在我們的例子中，它是3.3V。要將一個10位的ADC值轉成電壓值，我們使用下列公式：

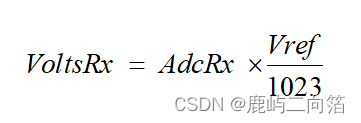
將3個軸的值代入上式，得到：

每個加速度計都有一個零加速度的電壓值，這個電壓值對應于加速度為0g。通過計算相對0g電壓的偏移量我們可以得到一個有符號的電壓值。比方說，0g電壓值VzeroG=1.65V，通過下面的方式可以得到相對0g電壓的偏移量:

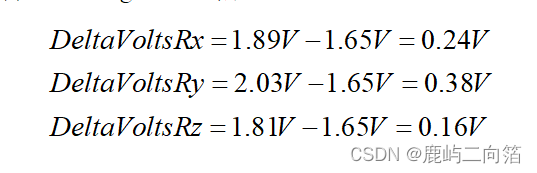
現在我們得到了加速度計的電壓值，但它的單位還不是g(9.8m/s^2)，最后的轉換，我們還需要引入加速度計的靈敏度，單位通常是mV/g。比如，加速度計的靈敏度Sensitivity = 478.5mV/g。靈敏度值可以在加速度計說明書中找到。要獲得最后的單位為g的加速度，我們使用下列公式計算：

綜上，可以把以上步驟用以下公式表達

現在我們得到了慣性力矢量的三個分量，如果設備除了重力外不受任何外力影響，那我們就可以認為這個方向就是重力矢量的方向。（自此明白了文獻[1]中所說只使用加速度計獲得的角度是基于飛行器在勻速飛行或靜止的條件下得到的）

圖2[引自網絡]

我們感興趣的角度是向量R和X，Y，Z軸之間的夾角，那就令這些角度為Axr，Ayr，Azr。觀察由R和Rx組成的直角三角形

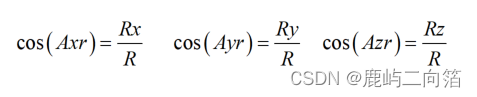
圖2中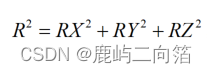，那么，角度即為

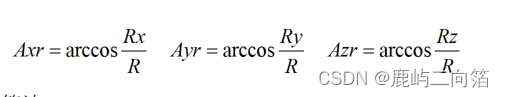
三、互補濾波算法

加速度計是極易受外部干擾的傳感器（如機械振動），但是測量值的誤差不隨時間的變化。陀螺儀輸出的角速度可以積分得到角度，動態性能好，受外部干擾小，但積分會造成誤差累積。可以看出，它們優缺點互補，結合起來才能有好的效果。

經典互補濾波算法（Classical Complementary Filter）

經典互補濾波算法基本原理是充分利用加速度計提供的低頻角度信號和陀螺儀提供的高頻角速度信號，對加速度計進行低通濾波，對陀螺儀進行高通濾波，分別濾出相應的干擾信號，為兩者的有效融合提供了很好的解決方案[2]。

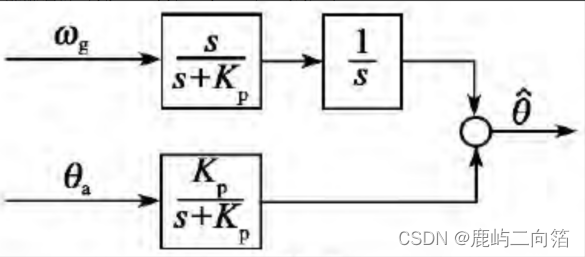
圖3 經典互補濾波算法—頻域形式原理圖[2]

融合后姿態角估計值為

其中，為陀螺儀測量的角速度，為加速度計測量的角度值，

為比例系數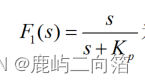，為高通濾波器，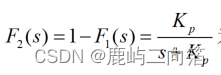

為低通濾波器。

圖4 經典互補濾波算法—時域形式原理圖[2]

對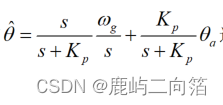

進行反拉氏變換，可得時域微分形式為

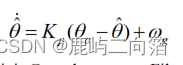
????改進后的互補濾波算法（Explicit Complementary Filter）

經典互補濾波算法實現簡單，但是估算精度角度較低，文獻[3]提出了一種改進算法（ECF），在經典互補濾波算法的補償環節加入積分器，以消除陀螺儀漂移常值誤差，原理框圖如下圖。

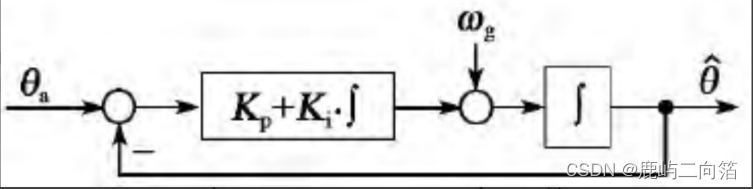
圖5 改進后的互補濾波算法[2]

時域微分形式為

?

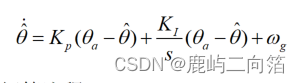
參考文獻

[1]?郭曉鴻,楊忠,陳喆,等. EKF和互補濾波器在飛行姿態確定中的應用[J]. 傳感器與微系統,2011,30(11):149-152.

[2] 傅忠云,朱海霞,孫金秋,等. 基于慣性傳感器 MPU6050 的濾波算法研究[J]. 壓電與聲光, 2015 (2015 年 05): 821-825,829.

[3] Mahony R, Hamel T, Pflimlin J M. Nonlinear complementary filters on the special orthogonal group[J]. IEEE Transactions on automatic control, 2008, 53(5): 1203-1218.

[4] Euston M, Coote P, Mahony R, et al. A complementary filter for attitude estimation of a fixed-wing UAV[C]//Intelligent Robots and Systems, 2008. IROS 2008. IEEE/RSJ International Conference on. IEEE, 2008: 340-345.

附程序：

void IMUupdate(float gx, float gy, float gz, float ax,float ay, float az)

{

????float norm;

????float vx, vy, vz;

????float ex, ey, ez;

????float q0q0 = q0*q0;

????float q0q1 = q0*q1;

????float q0q2 = q0*q2;

????float q1q1 = q1*q1;

????float q1q3 = q1*q3;

????float q2q2 = q2*q2;

????float q2q3 = q2*q3;

????float q3q3 = q3*q3;

????if(ax*ay*az==0)

????????return;

????// 第一步：對加速度數據進行歸一化

????norm = sqrt(ax*ax + ay*ay + az*az);

????ax = ax / norm;

????ay = ay / norm;

????az = az / norm;

????// 第二步：DCM矩陣旋轉

????vx = 2*(q1q3 - q0q2);

????vy = 2*(q0q1 + q2q3);

????vz = q0q0 - q1q1 - q2q2 + q3q3 ;

????// 第三步：在機體坐標系下做向量叉積得到補償數據

????ex = ay*vz - az*vy ;

????ey = az*vx - ax*vz ;

????ez = ax*vy - ay*vx ;

????// 第四步：對誤差進行PI計算，補償角速度

????exInt = exInt + ex * Ki;

????eyInt = eyInt + ey * Ki;

????ezInt = ezInt + ez * Ki;

????gx = gx + Kp*ex + exInt;

????gy = gy + Kp*ey + eyInt;

????gz = gz + Kp*ez + ezInt;

????// 第五步：按照四元數微分公式進行四元數更新

????q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;

????q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;

????q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;

????q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;

}

?