---

前言

在上一篇文章中，介紹了VAD對于能量的計算原理和策略介紹。本篇文章中講進一步介紹VAD中的人聲/噪聲決策，這是基于高斯混合模型，也就是GMM進行計算的。

本篇文章將會對照源碼、結合圖像進行介紹：

• GMM模型介紹（可以跳過）
• webrtc中VAD的高斯模型（包括來源以及使用）
• 人聲/噪聲決策以及在線更新機制
• hangover機制

本篇文章比較長，可以耐心觀看。

|版本聲明：山河君，未經博主允許，禁止轉載

---

一、高斯混合模型介紹

如果對于高斯模型很熟悉那么可以跳過這一節，這里需要明白的是概率密度、區間概率和條件概率的區別。

1.高斯模型舉例

1）定義

高斯分布（又叫正態分布）是一種常見的概率分布，它的概率密度也叫做似然函數（PDF）是：
$$p(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (?\frac{(x?\mu {)}^2}{2{\sigma }^2})$$

• $\mu$為均值：分布的中心位置，數據大部分集中在它附近。
• ${\sigma }^2$表示方差：分布的寬度，數值越大，圖像分布越平；數值越小，分布越尖。

而使用高斯分布計算區間概率公式為：
$$P(a<X<b)={\int }_a^{b}p(x)dx$$

2）舉例說明

假設有一門數學考試，100 分滿分，有5個學生的成績分別是$60,70,80,75,65$：

• 均值$\mu$：$\mu =\frac{1}{N}{\sum }_{i=1}^N{x}_i=\frac{60+70+80+75+65}{5}=70$
• 方差${\sigma }^2=\frac{1}{N}{\sum }_{i=1}^N(x_i?\mu {)}^2=\frac{(?10{)}^2+0^2+10^2+5^2+(?5{)}^2}{5}=50$

那么現在還有一個學生

• 他的成績為$73$分的概率帶入公式最終結果為：$5.16\%$
• 他的成績在$[70,75]$分之間的概率帶入公式為：$26\%$

2.高斯混合模型(GMM)

1）定義

GMM 就是多個高斯分布的加權和，它的概率密度公式是:
$$p(x)=\sum _{k=1}^K{w}_k?\mathrm{N}(x|u_k,{\sigma }_k^2)$$

• $k$：高斯分布的個數
• $w_k$：每個分布的權重（比例，所有權重相加 = 1）
• $u_k,{\sigma }_k$：第k 個高斯分布的均值和方差
• $\mathrm{N}(x|u_k,{\sigma }_k^2)$：第k個高斯分布的概率密度函數 (PDF)

而此時我們計算某一個值屬于哪一個高斯分布的過程叫做條件概率（責任度）：
$$P(l_k|x)=\frac{l_k}{p(x)}=\frac{w_k?\mathrm{N}(x|u_k,{\sigma }_k^2)}{p(x)}$$

2）舉例說明

上文中是一個以成績的例子進行計算高斯分布，但顯然現實中要考慮的因素會更多：

• 一部分學生是學霸$30\%$，集中在$85\pm 5$分附近
• 一部分學生是普通學生$70\%$，集中在$65\pm 10$分附近

那么由此可以得到：

• 學霸群體：均值$u_1=85$，標準差${\sigma }_1=5$，權重$w_1=0.3$
• 普通學生：均值$u_2=65$，標準差${\sigma }_2=10$，權重$w_2=0.7$

此時有一個學生成績為70，那么他的條件概率分別為：

• $P(l_1|x)=\frac{l_1}{p(x)}\approx 0.01067(1.07\%)$
• $P(l_2|x)=\frac{l_2}{p(x)}=1?P(l_1|x)\approx 0.98933(98.93\%)$

很明顯，該學生大概率屬于普通學生

3）一維曲線

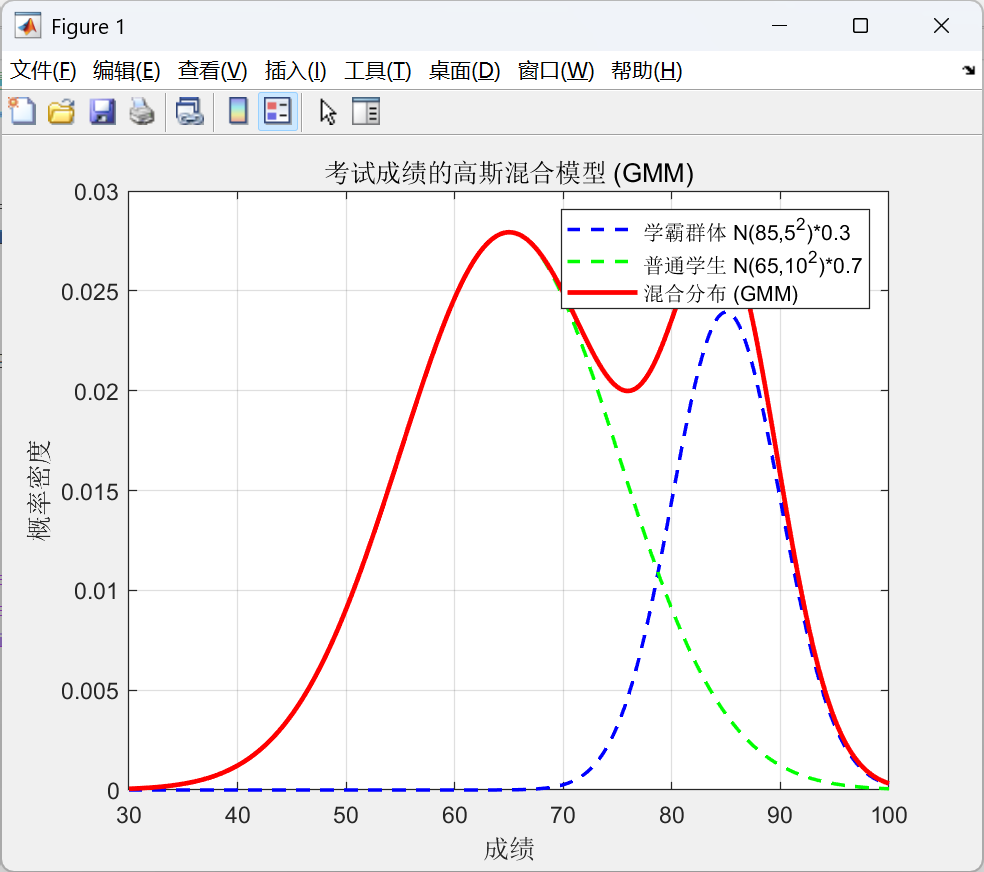
使用matlab畫出曲線

x = linspace(30, 100, 500);% 學霸群體參數
mu1 = 85; sigma1 = 5; w1 = 0.3;
pdf1 = w1 * normpdf(x, mu1, sigma1);% 普通學生群體參數
mu2 = 65; sigma2 = 10; w2 = 0.7;
pdf2 = w2 * normpdf(x, mu2, sigma2);% 混合分布
pdf_mix = pdf1 + pdf2;% 繪制
figure;
plot(x, pdf1, 'b--', 'LineWidth', 1.5); hold on;
plot(x, pdf2, 'g--', 'LineWidth', 1.5);
plot(x, pdf_mix, 'r-', 'LineWidth', 2);
grid on;
legend('學霸群體 N(85,5^2)*0.3', ...'普通學生 N(65,10^2)*0.7', ...'混合分布 (GMM)');
title('考試成績的高斯混合模型 (GMM)');
xlabel('成績');
ylabel('概率密度');

二、VAD高斯混合模型

1.模型訓練介紹

1）訓練方法

webrtc關于VAD的高斯混合模型訓練是一種離線訓練，是通過以下幾個步驟得到的：

• 準備數據
  • 收集了大量的語音數據（各種語言、男女聲、不同音量）
  • 收集了大量的噪聲數據（白噪聲、街道、辦公室、電話線路噪聲等）
• 特征提取
  • 對每一幀音頻（10ms ~ 30ms）提取簡單特征：子帶能量、總能量、過零率
  • 特征維度很低，不像是MFCC會有多個維度，但適合在嵌入式環境運行
• 擬合高斯分布
  • 把“語音幀特征”丟進一個高斯混合模型訓練器
  • 把“噪聲幀特征”丟進另一個 GMM 訓練器
  • 使用EM算法迭代得到每個分量的均值、方差、權重
• 量化和存儲
  • 得到的均值、方差、權重定點數存儲（int16_t），方便在 C 代碼里運行
  • 該套參數固定寫死在代碼表里，運行時雖然會根據實際情況修改，但不會在運行后進行存儲

由此我們也可以直覺看出來這套模型的明顯的優缺點：

特性	優點	缺點
計算效率	高，適合實時	無
模型復雜度	低，易實現	表達能力有限
多模態表示	可以區分靜音/語音	只適合簡單多模態
魯棒性	可自適應噪聲變化	對異常噪聲敏感
時序建模	無	需要額外平滑

2）訓練結果

webrtc中訓練后的結果是以Q7格式分別存儲在：

• kNoiseDataWeights：噪聲的兩個高斯分布權重，表格中的G0和G1
• kNoiseDataMeans：噪聲的兩個高斯分布均值
• kNoiseDataStds：噪聲的兩個高斯分布的方差
• kSpeechDataWeights：噪聲的兩個高斯分布權重，表格中的G0和G1
• kSpeechDataMeans：噪聲的兩個高斯分布均值
• kSpeechDataStds：噪聲的兩個高斯分布的方差
• G0：低幅度、常見特征，是頻帶特征里的主分量
• G1：高幅度、變化性更大的特征，是頻帶特征里的補充分量

頻帶	高斯	Noise 權重	Speech 權重	Noise 均值	Speech 均值	Noise Std	Speech Std
0	G0	34	48	6738	8306	378	555
	G1	62	82	4892	10085	1064	505
1	G0	72	45	7065	10078	493	567
	G1	66	87	6715	11823	582	524
2	G0	53	50	6771	11843	688	585
	G1	25	47	3369	6309	593	1231
3	G0	94	80	7646	9473	474	509
	G1	66	46	3863	9571	697	828
4	G0	56	83	7820	10879	475	492
	G1	62	41	7266	7581	688	1540
5	G0	75	78	5020	8180	421	1079
	G1	103	81	4362	7483	455	850

在代碼中，將會在WebRtcVad_InitCore接口中存儲在VadInstT結構體中。

2.噪聲高斯模型分布

下面將根據具體的參數，畫出6個子帶的兩個高斯分布G0，G1圖像，然后再根據權重進行G0和G1加權后的高斯混合圖像。

1）matlab代碼

clc; clear; close all;% 原始 Q7 數據
kNoiseDataMeans_Q7   = [6738, 4892, 7065, 6715, 6771, 3369, 7646, 3863, 7820, 7266, 5020, 4362];
kNoiseDataStds_Q7    = [378, 1064, 493, 582, 688, 593, 474, 697, 475, 688, 421, 455];
kNoiseDataWeights_Q7 = [34, 62, 72, 66, 53, 25, 94, 66, 56, 62, 75, 103];% 轉為 Q0（浮點）
kNoiseDataMeans   = double(kNoiseDataMeans_Q7) / 128;
kNoiseDataStds    = double(kNoiseDataStds_Q7) / 128;
kNoiseDataWeights = double(kNoiseDataWeights_Q7);   % 權重本身可以直接使用kTableSize = length(kNoiseDataMeans);
numBands = kTableSize / 2;figure;for band = 1:numBands% 提取 G0, G1 的參數mean0 = kNoiseDataMeans(2*band-1);mean1 = kNoiseDataMeans(2*band);std0  = kNoiseDataStds(2*band-1);std1  = kNoiseDataStds(2*band);weight0 = kNoiseDataWeights(2*band-1);weight1 = kNoiseDataWeights(2*band);% x 范圍，取 ±4σx_min = min(mean0-4*std0, mean1-4*std1);x_max = max(mean0+4*std0, mean1+4*std1);x = linspace(x_min, x_max, 500);% 高斯分布G0 = (1/(std0*sqrt(2*pi))) * exp(-0.5*((x-mean0)/std0).^2);G1 = (1/(std1*sqrt(2*pi))) * exp(-0.5*((x-mean1)/std1).^2);% 加權混合Gmix = (weight0*G0 + weight1*G1) / (weight0 + weight1);% 繪圖subplot(2,3,band);plot(x, G0, 'b', 'LineWidth',1.5); hold on;plot(x, G1, 'r', 'LineWidth',1.5);plot(x, Gmix, 'k--', 'LineWidth',1.5);title(['Subband ' num2str(band)]);legend('G0','G1','G_{mix}');xlabel('Value'); ylabel('Probability Density');
end

2）結果

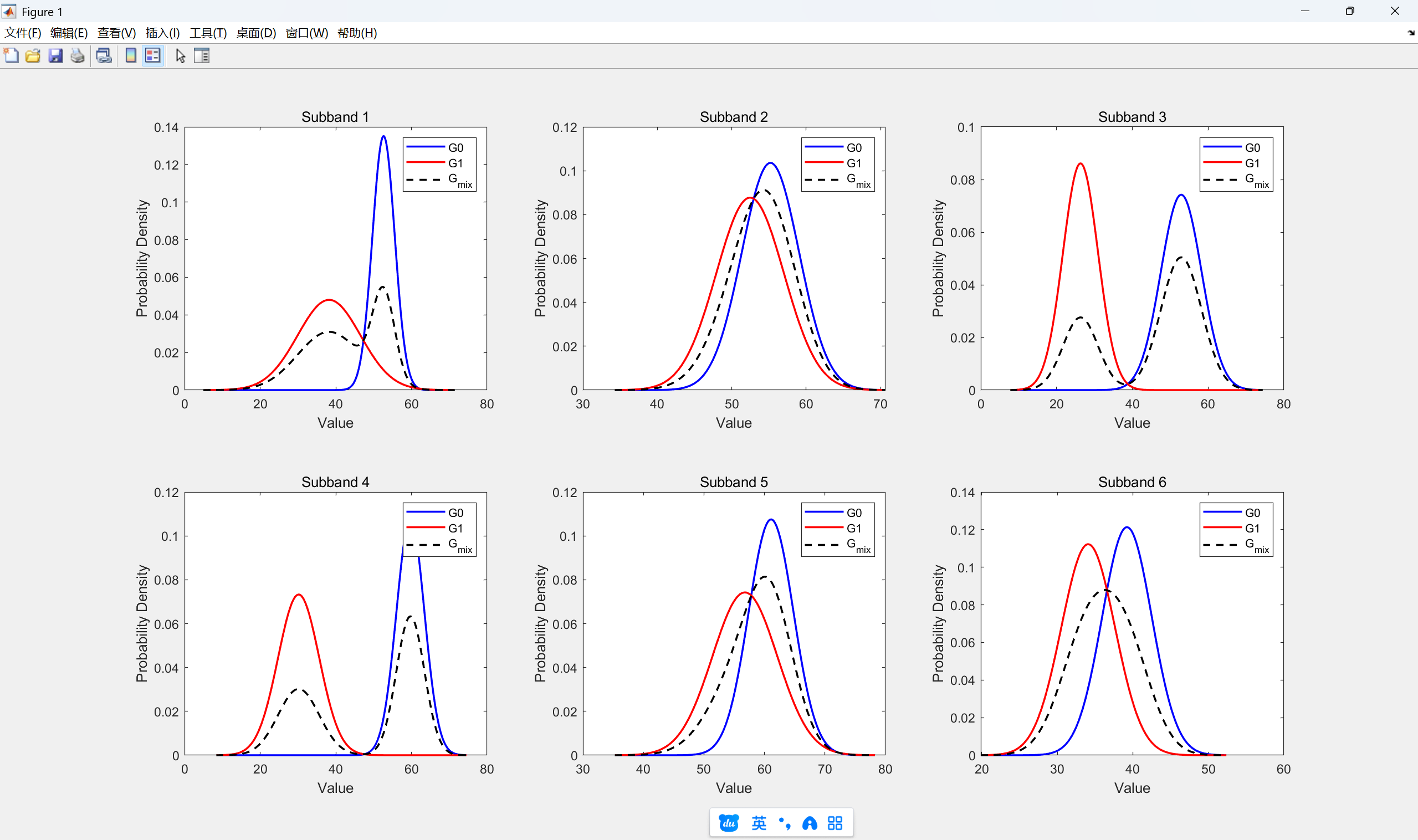
2.人聲高斯模型分布

和計算噪聲高斯模型分布一樣，只需要將matlab中代碼替換即可，這里就不貼出代碼，直接看結果：

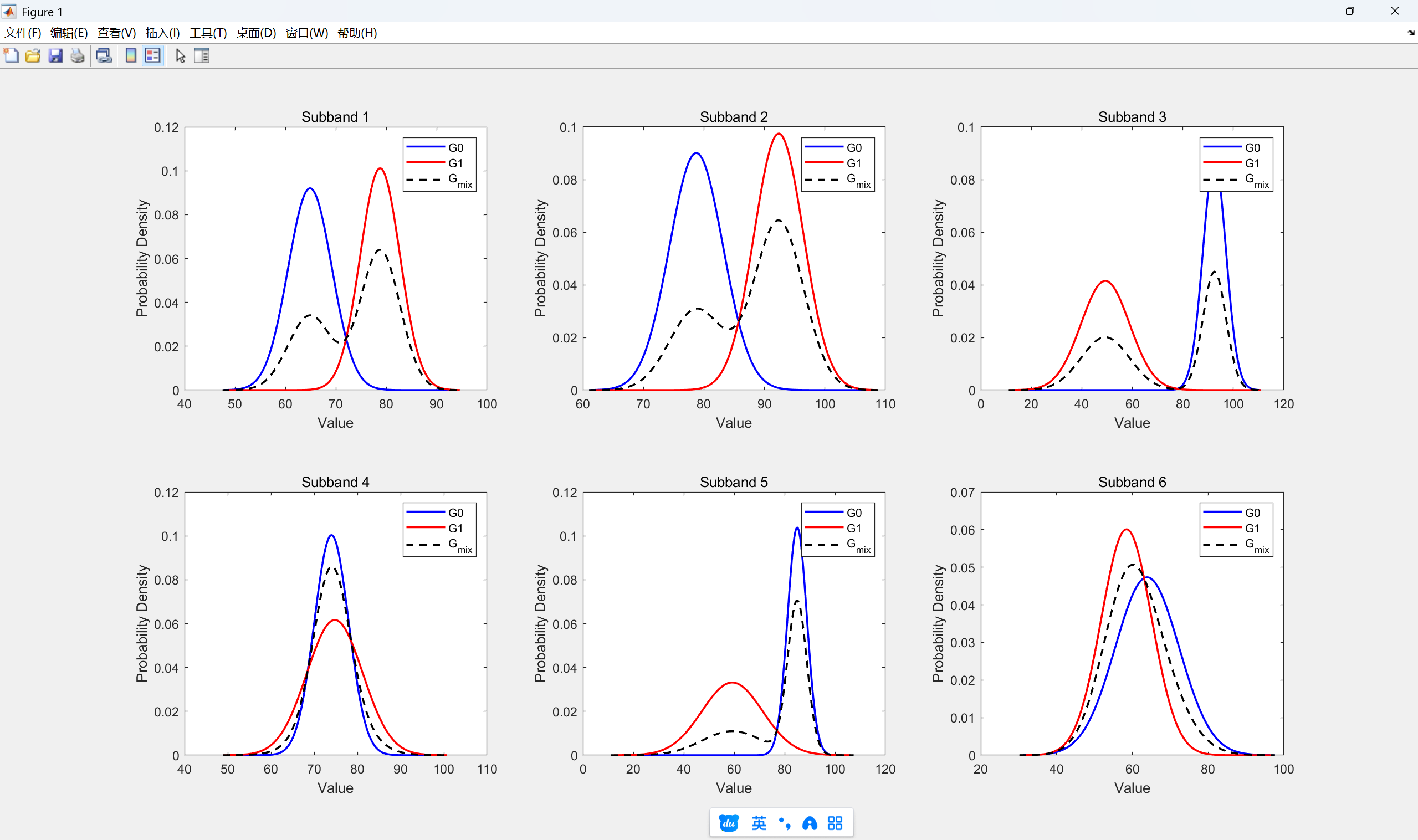
三、VAD人聲判斷

在上一篇文章webrtc之語音活動上——VAD能量檢測原理以及源碼詳解中，我們已經知道了：

• 檢測模式的區別
• 幀長劃分方法
• 6個非等寬頻帶的能量
• 頻帶劃分的意義

1.高斯分布計算

1）公式

源碼中關于PDF計算使用Q格式運算以保證精度，其計算公式為：
$$\frac{1}{\sigma }?\exp (?\frac{(x?m{)}^2}{2?{\sigma }^2})$$
該接口的計算方式少了一個$\sqrt{2\pi }$，并且這里同樣將$\log$運算簡化，因此它是一個相對值（比例），而縮放后的 PDF是用于相對比較，不是嚴格的概率密度，不會影響后續決策與更新。

2）對應代碼

接口名為WebRtcVad_GaussianProbability，以下是參數和返回值：

• input：頻帶能量，以Q4格式保存
• mean：噪聲/人聲的高斯均值，Q7格式
• std：噪聲/人聲的高斯方差，Q7格式
• delta：$\frac{x?m}{s^2}$，用于后續更新模型，Q11格式
• 返回值：概率密度，Q20格式

2.人聲判定策略

1）判斷機制

VAD判斷人聲是雙重機制：

• 局部判定： 捕捉某個子帶特別強烈的語音
• 全局判定：要求整體證據夠強
• 最終決策：兩者取 OR，既保證靈敏度，又保證魯棒性

2）重要閾值確認

在設置模式WebRtcVad_set_mode_core接口里，確定

• individual：單個頻帶人聲閾值范圍，用于局部判定
• total：整體人聲閾值閾值范圍，用于整體

而對于不同幀長再進一步確定閾值，這里是在GmmProbability真正進行決策的地方進行確定。而對于：

• 短幀10ms：由于信息少，則使用高閾值以避免誤判
• 中等20ms：閾值低，放寬一些
• 長幀30ms：本身信息穩定，為了避免太寬松 又設高

除此之外，在進行全局判定時，不同頻帶的權重存儲在kSpectrumWeight中。

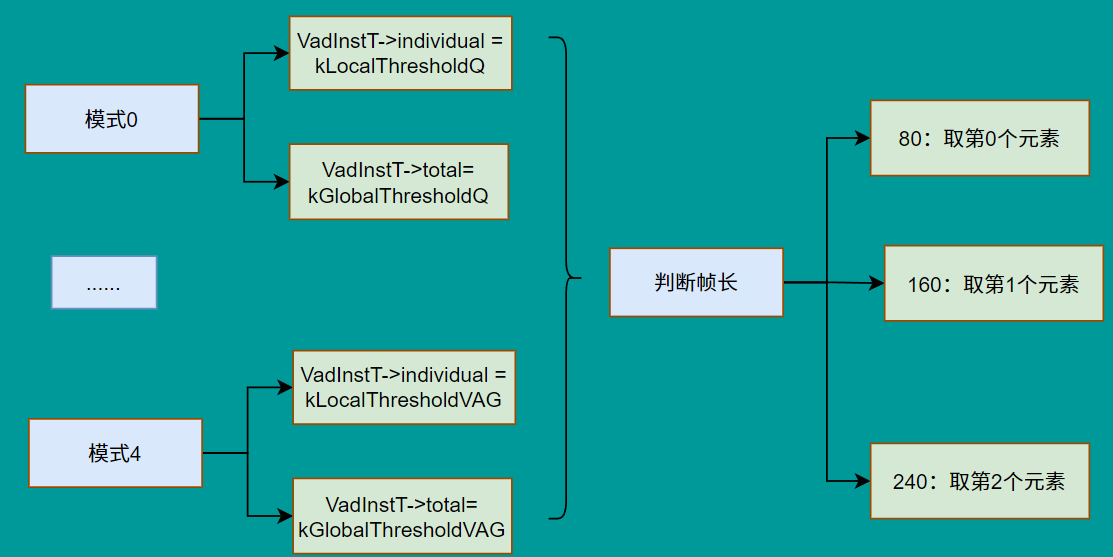
值得注意的是，這些閾值的由來是根據大規模實驗 + ROC 曲線分析 + 主觀聽感測試 手工調出來的經驗值。

3）整體流程

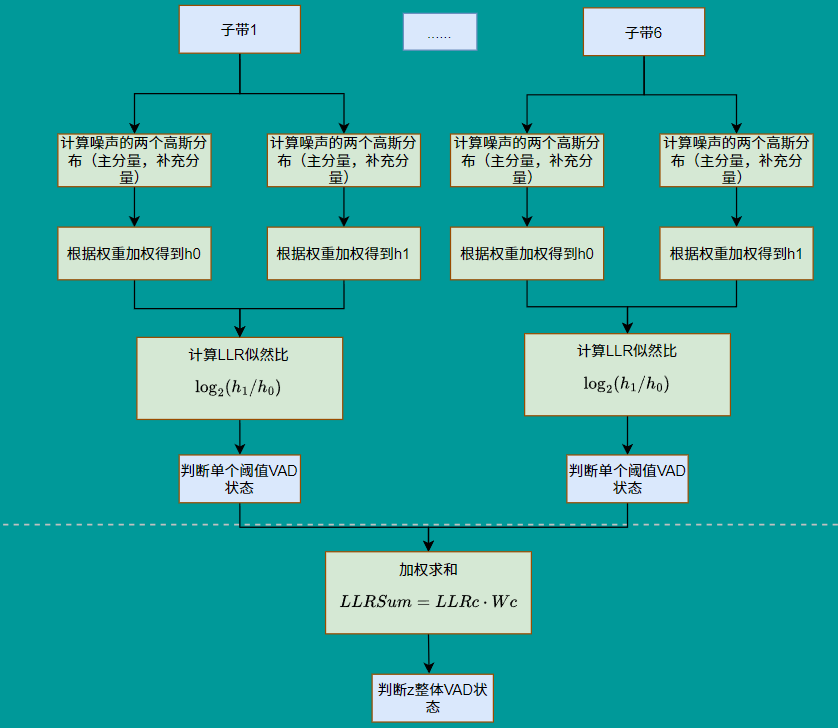
第一步：計算噪聲/人聲概率分布

同一段頻帶語音根據噪聲/人聲的高斯參數，分別進行計算主分量/補充分量的概率分布，再根據權值計算真正的概率密度，代碼如下：

for (channel = 0; channel < kNumChannels; channel++) {h0_test = 0;h1_test = 0;for (k = 0; k < kNumGaussians; k++) {gaussian = channel + k * kNumChannels;tmp1_s32 = WebRtcVad_GaussianProbability(features[channel],self->noise_means[gaussian],self->noise_stds[gaussian],&deltaN[gaussian]);noise_probability[k] = kNoiseDataWeights[gaussian] * tmp1_s32;h0_test += noise_probability[k];  // Q27tmp1_s32 = WebRtcVad_GaussianProbability(features[channel],self->speech_means[gaussian],self->speech_stds[gaussian],&deltaS[gaussian]);speech_probability[k] = kSpeechDataWeights[gaussian] * tmp1_s32;h1_test += speech_probability[k];  // Q27}

第二步：噪聲/人聲比較

判斷單個頻帶是否為人聲使用的是似然對數比，也就是$\log 2(\frac{Pr(X|H1)}{Pr(X|H0)})$，這么做的好處是：

• 避免概率數值太小引起數值問題
• LLR 的加和性質，可以進行多個頻帶綜合判定

值得注意的是：這近似在數幀平均下通常偏差較小，但對極端 / 較小樣本會產生偏差，所以后面通過局部+全局、hangover機制與模型更新來抵消誤判。

這里的移位操作是為了簡化$\log$運算，用最高位表示為整數部分，用整數位的差值來近似$\log 2(h1/h0)$，核心代碼為：

      shifts_h0 = WebRtcSpl_NormW32(h0_test);shifts_h1 = WebRtcSpl_NormW32(h1_test);if (h0_test == 0) {shifts_h0 = 31;}if (h1_test == 0) {shifts_h1 = 31;}log_likelihood_ratio = shifts_h0 - shifts_h1;

第三步：判斷單個閾值

如果單個頻帶的信號人聲強烈，將會直接認定為語音，值得注意的是即使判斷為人聲了，還是會接著計算其他頻帶，這是為了更新模型。核心代碼為：

if ((log_likelihood_ratio * 4) > individualTest) {vadflag = 1;}

第四步：全局判定

這里分為兩部分

• 根據權重加合
• 整體閾值判斷

其核心代碼如下：

sum_log_likelihood_ratios +=(int32_t) (log_likelihood_ratio * kSpectrumWeight[channel]);.......vadflag |= (sum_log_likelihood_ratios >= totalTest);         

四、模型更新

在進行模型更新時，需要考慮到平滑處理，所以這里運用到大量的平滑濾波的思想，見文章語音信號處理三十一——常用的時域/頻域平滑濾波。

1.計算條件概率

首先獲取各個頻帶噪聲/人聲在主分量和補充分量的條件概率，分別存儲在ngprvec和sgprvec中。

如果$h<0$，那么默認該數值必然是主分量特征，以下是噪聲的條件概率核心代碼，人聲類似：

h0 = (int16_t) (h0_test >> 12);  // Q15if (h0 > 0) {tmp1_s32 = (noise_probability[0] & 0xFFFFF000) << 2;  // Q29ngprvec[channel] = (int16_t) WebRtcSpl_DivW32W16(tmp1_s32, h0);  // Q14ngprvec[channel + kNumChannels] = 16384 - ngprvec[channel];} else {ngprvec[channel] = 16384;}

2.獲取噪聲基線和均值

1）噪聲基線的作用

WebRTC VAD 和很多能量型 VAD 都是基于一個基本假設：在連續音頻信號中，語音的能量通常高于環境噪聲的能量。

而噪聲基的含義是指：環境噪聲在短時間或一段時間內的平均能量水平或特征值參考。

2）確定噪聲基線

噪聲基線的獲取是一種中值濾波的思想。在接口WebRtcVad_FindMinimum中，它的大致流程為：

輸入: feature_value, channel, self┌─? [1] 更新歷史值的年齡
│      ├─ 遍歷16個存儲的最小值
│      ├─ age < 100 → age++
│      └─ age == 100 → 移除該值，數組前移，最后位置填充大數
│
└─? [2] 判斷是否插入新值├─ feature_value 比數組中的某些值小│     └─ 找到插入位置 position│          └─ 從尾部往后移，插入新值，age=1└─ 否則丟棄（說明它不是最小16個之一）┌─? [3] 計算當前中位數
│      ├─ frame_counter > 2 → 取 smallest_values[2] (第3小)
│      └─ frame_counter <= 2 → 取 smallest_values[0] (最小值)
│
└─? [4] 平滑更新 mean_value[channel]├─ 如果 current_median < mean_value → α = 0.2 (快速下降)└─ 否則 α = 0.99 (緩慢上升)└─ mean_value[channel] ← α * mean_value[channel] + (1-α) * current_median[5] 返回 mean_value[channel]

這里可以對照代碼進行理解。

3）獲取噪聲均值

實現主要在WeightedAverage接口內，該接口的使用方法為：

• 輸入主分量和補充分量的均值
• 輸入對應的權重
• 輸出計算后的均值

3.更新噪聲均值

1）短時更新

WebRTC 里不可能每次都存很多幀再做完整的EM，并且GMM更新中webrtc希望帶權，所以這里采用的是梯度遞推進行更新，公式為：
$${\mu }_{noise}^{now}={\mu }_{noise}^{old}+\eta ?{\gamma }_{now}(x?{\mu }_{noise}^{old})$$

• $\eta$：權系數
• ${\gamma }_{now}$：當前頻帶當前分量的條件概率

由于篇幅原因，這里不做推導了，可以看看別的文章，或者可以私信博主

這里加權是并不希望噪聲平均變化過快。對應代碼為：

static const int16_t kNoiseUpdateConst = 655; // Q15
nmk2 = nmk;
if (!vadflag) {delt = (int16_t)((ngprvec[gaussian] * deltaN[gaussian]) >> 11);nmk2 = nmk + (int16_t)((delt * kNoiseUpdateConst) >> 22);
}

2）平滑修正

首先會用噪聲基線減去頻帶噪聲均值得到差值，再根據差值進行指數加權移動平均的思想，和當前幀的噪聲均值相加為下一幀的噪聲均值，對應代碼：

ndelt = (feature_minimum << 4) - tmp1_s16;
nmk3 = nmk2 + (int16_t)((ndelt * kBackEta) >> 9);

值得注意的是：平滑修正不受vadflag影響

3）邊界約束

即強制噪聲均值不能小于某個最小值，和防止噪聲均值過大，避免它被語音能量無限拉升。代碼如下：

tmp_s16 = (int16_t) ((k + 5) << 7);if (nmk3 < tmp_s16) {nmk3 = tmp_s16;}tmp_s16 = (int16_t) ((72 + k - channel) << 7);if (nmk3 > tmp_s16) {nmk3 = tmp_s16;}

4）策略意義

對于nmk2會受到$\gamma$的影響，而$\gamma$并不是固定常數，而是隨著當前幀的條件概率變動，一旦語音能量進入，更新方向就會發生錯誤。此時平滑修正的意義就體現出來：

• 短時更新可能受到語音污染，可能偏離真實噪聲基線
• 如果當前幀判定為非噪聲，那么均值會被kBackEta慢慢收斂回長期基線

4.更新人聲均值

和更新噪聲均值一樣的梯度更新計算方法，只是區別是：

• 不需要進行長期拉回，因為人聲是特征動態明顯，不需要噪聲基線作為參考
• 噪聲的限幅控制是為了保證模型穩定，避免漂移到語音區，而人聲限幅是跟隨語音分布變化，防止過度漂移，所以限幅范圍不同
• 人聲均值向上取整而不是向下取整smk2 = smk + ((tmp_s16 + 1) >> 1);

5.更新人聲方差

1）更新公式

和上文一樣，這里采用的是遞推更新：
$${\sigma }_{new}={\sigma }_{old}+\eta ?\frac{w_k}{{\sigma }_{old}}(\frac{(x?{\mu }_{old}^2)}{{\sigma }_{old}^2}?1)$$

2）代碼解析

tmp_s16 = ((smk + 4) >> 3);tmp_s16 = features[channel] - tmp_s16;  tmp1_s32 = (deltaS[gaussian] * tmp_s16) >> 3;tmp2_s32 = tmp1_s32 - 4096;tmp_s16 = sgprvec[gaussian] >> 2;tmp1_s32 = tmp_s16 * tmp2_s32;tmp2_s32 = tmp1_s32 >> 4; if (tmp2_s32 > 0) {tmp_s16 = (int16_t) WebRtcSpl_DivW32W16(tmp2_s32, ssk * 10);} else {tmp_s16 = (int16_t) WebRtcSpl_DivW32W16(-tmp2_s32, ssk * 10);tmp_s16 = -tmp_s16;}tmp_s16 += 128;  // Rounding.ssk += (tmp_s16 >> 8);

其中：

• $w_k$：來自于sgprvec
• $\eta$：為0.025，代碼中體現在WebRtcSpl_DivW32W16產生了0.1的分母，sgprvec[gaussian] >> 2產生了4的分母
• tmp_s16 = ((smk + 4) >> 3)：這里的加4原因是為了保證右移3位是向上取整保存精度

3）邊界約束

方差值不能小于384

static const int16_t kMinStd = 384;
if (ssk < kMinStd) {ssk = kMinStd;}

6.更新噪聲方差

和更新人聲方差一樣，區別在于更新步長的大小是根據偏移量決定的，不過范圍大致在0.015～0.02 之間。

7.模型分離

為了防止speech GMM 模型和 noise GMM 模型的均值太接近而粘在一起，需要最終結合兩者進行決策。

1）計算全局均值

noise_global_mean  = WeightedAverage(&self->noise_means[channel], 0, &kNoiseDataWeights[channel]);
speech_global_mean = WeightedAverage(&self->speech_means[channel], 0, &kSpeechDataWeights[channel]);

• 對每個 channel，把各個高斯分量的均值做加權平均。
• 得到一個 全局 noise 平均值 和一個 全局 speech 平均值。

2）計算差值

diff = (int16_t)(speech_global_mean >> 9) - (int16_t)(noise_global_mean >> 9);

• speech 全局均值 ? noise 全局均值。
• 如果差值太小，說明兩個模型過于接近

3）如果模型太近，強行拉開

if (diff < kMinimumDifference[channel]) {tmp_s16 = kMinimumDifference[channel] - diff;// tmp1_s16 ≈ 0.8 * (缺口)// tmp2_s16 ≈ 0.2 * (缺口)// 把 speech 模型整體往上推一點speech_global_mean = WeightedAverage(&self->speech_means[channel],tmp1_s16, &kSpeechDataWeights[channel]);// 把 noise 模型整體往下拉一點noise_global_mean  = WeightedAverage(&self->noise_means[channel],-tmp2_s16, &kNoiseDataWeights[channel]);
}

• 如果 gap 太小，就把 speech 往上推 80%，noise 往下拉 20%，強制保持至少 kMinimumDifference 的區分度。
• 這樣避免兩個模型均值重疊，保持判決的魯棒性。

4）限制模型漂移范圍

if (speech_global_mean >> 7 > kMaximumSpeech[channel]) {// speech 上限...
}
if (noise_global_mean >> 7 > kMaximumNoise[channel]) {// noise 上限...
}

作用是給 speech 和 noise 均值設上界，避免模型被極端值推得太遠。

五、hangover 機制

1.策略作用

WebRTC VAD 的hangover 機制，用來在語音剛結束時 延長一小段時間繼續判為語音，避免抖動。

2.整體流程

檢測到語音 → num_of_speech++├─ 如果 num_of_speech <= kMaxSpeechFrames → over_hang = overhead1└─ 如果 num_of_speech >  kMaxSpeechFrames → over_hang = overhead2檢測到非語音├─ 如果 over_hang > 0 → 繼續輸出語音, over_hang--└─ 如果 over_hang = 0 → 輸出靜音

其中：

• overhead1：給短語音的尾巴加一點點余量。
• overhead2：給長語音的尾巴加更長的余量。
• num_of_speech：用來區分當前語音段的“長/短”。
• over_hang：用來平滑語音和靜音的切換，防止“斷斷續續”

3.對應代碼

1）非語音處理

if (!vadflag) {if (self->over_hang > 0) {vadflag = 2 + self->over_hang;self->over_hang--;}self->num_of_speech = 0;
}

• 但 hangover 計數器 over_hang > 0：說明前面剛有語音 → 進入“延長語音”階段

  • 把 vadflag 設置為 2 + self->over_hang（這里 2 是特殊標記，表明這不是直接檢測出的語音，而是 hangover 延長出來的語音）
  • over_hang--：計數器遞減

• 否則就徹底當作 silence

• num_of_speech = 0：清零語音幀計數器

2）語音

else {self->num_of_speech++;if (self->num_of_speech > kMaxSpeechFrames) {self->num_of_speech = kMaxSpeechFrames;self->over_hang = overhead2;} else {self->over_hang = overhead1;}
}

• num_of_speech++：累計連續語音幀數
• 如果超過 kMaxSpeechFrames（最大語音幀數限制）：
  • 把 num_of_speech 固定到上限
  • over_hang = overhead2（長的 hangover 時間）
• 否則：over_hang = overhead1（短的 hangover 時間）

---

總結

WebRTC VAD 展示了一個典型的“經典信號處理 + 工程優化”方案：

• 在特征層面，采用子帶能量的對數刻畫，使得語音與噪聲分布更接近高斯；
• 在模型層面，使用固定參數的雙高斯混合模型，結合局部和全局判決，提高魯棒性；
• 在實現層面，大量利用 Q 格式、移位近似、預計算表，保證了低算力環境下的實時性；
• 在動態性上，通過逐幀更新和邊界約束，使模型能逐漸適應環境變化。

當然，這種基于 GMM 的方法也有局限：在強噪聲、非平穩噪聲環境下可能誤判，且閾值調優高度依賴經驗。隨著算力提升，DNN/RNN 基的 VAD 在魯棒性上表現更優，但代價是更高的復雜度與延遲。

反正收藏也不會看，不如點個贊吧！