我已經兩年沒有碰過深度學習了，寫此文記錄學習過程，加深理解。

再次深入學習深度學習|花書筆記1

這本書說的太繁瑣了，如果是想要基于這本書入門深度學習，大可不必。但是可以用來回爐再造，加深理解。

信息論

研究一個信號中信息包含多少的量化，在實際工作中，可以用到信息熵這種東西，約束生成的東西是精簡的，合理的。

• 一個基本想法：發生的概率P(x)越低，說明信息量越大。發生概率是1，那么包含的信息量就是0了。
• 信息量的單位是奈特(nats).就是一個傳遞了1/e的發生概率的事件的信息。
• 當對數的底數是2，信息的單位就是bit比特。

I(x)=-log(P(x))  
1 nats= -log(1/e)
1 bit= -log(1/2)

• 交叉熵，p,q是真實分布和非真實分布
  
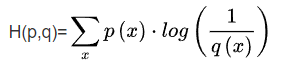
• 歸一化 保證所有元素的和為1.用在預處理階段，不知道這種說法對不對，就是輸入數據符合標準正態分布，也就是收到0-1之間再做正態分布。這可以應用在圖像，聲音，文本，具體的似乎是在數據集內進行操作。

第四節 數值計算中的問題

上溢出 和 下溢出

主要來自于計算機數字表示中的位數限制，接近0時候導致數值被舍為0；過大時導致近似為∞。
使用softmax激活函數。

    def softmax(x):e_x = np.exp(x - np.max(x))return e_x / np.sum(e_x)

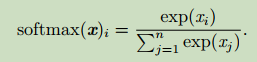
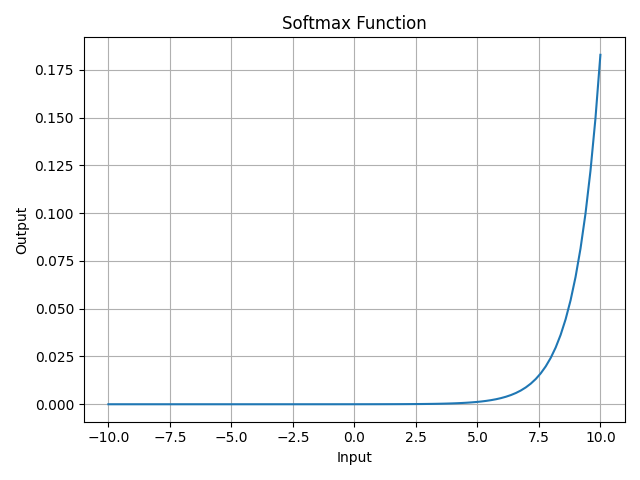
病態條件

當我們說一個數學名詞是病態時，這個詞意味著改動很小時擾動很大。包括病態方程組。
這可能對數據的精度有一定要求。
即使我們計算正確， 病態條件的矩陣也會放大預先存在的誤差。
三點

• 梯度消失
• 梯度爆炸
• 梯度過緩

優化法

目的：最大化或最小化Loss函數/損失函數/代價函數/誤差函數
方法：梯度下降法

f(x+t)近似f(x)+t*f'(x)
當t足夠小？似乎是有這個條件的

最終到達如圖所示的某個極值點，當然很可能是局部最優解。

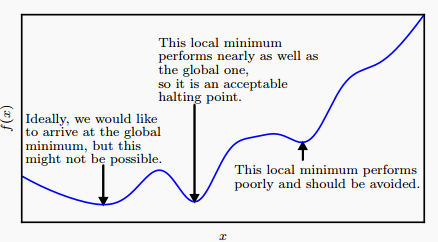
基本的兩個點是

• 如果有多個參數就求偏導
• 每次優化的步長隨著訓練時間的延長而縮小
  這是在連續函數中的梯度優化算法，在離散函數中有叫爬山算法的東西，沒有了解過。

由于梯度下降法的步長t并非數學定義下的無窮小量，梯度下降方向實際上并非一個嚴格的最優方向。
可以采用二階導數 Hessian 矩陣/牛頓法優化梯度下降算法。