第十六屆藍橋杯軟件賽 C 組省賽 C++ 題解

大家好，今天是 2025 年 9?月 11 日，我來給大家寫一篇關于第十六屆藍橋杯軟件賽 C 組省賽的C++ 題解，希望對大家有所幫助！！！

創作不易，別忘了一鍵三連

題目一：數位倍數

題目鏈接：數位倍數

【題目描述】

【算法原理】

簽到題、枚舉、數位拆分

只需要暴力枚舉 1 到 202504 之間的所有整數，對于每一個整數，拆分它的每一位求和之后看看是不是 5 的倍數就可以了。

至于如何拆分一個整數的每一位，相信大家已經掌握的非常熟練了，直接來看代碼。

【代碼實現】

#include <iostream>using namespace std;bool check(int x)
{int sum = 0; // 統計每一個數的數位和while(x){sum += x % 10;x /= 10;}return sum % 5 == 0;
}int main()
{int cnt = 0;for(int i = 1; i <= 202504; i++)if(check(i))cnt++;cout << cnt << endl; return 0;
}

題目二：2025

題目鏈接：2025

【題目描述】

【算法原理】

簽到題、枚舉、數位拆分

和題目一類似，只需要暴力枚舉 1 到 20250412 之間的所有整數，對于每一個整數，拆分它的每一位并統計，之后看看是不是含有至少 1 個 0，2 個 2，1 個 5 就可以了。

至于如何拆分一個整數的每一位，相信大家已經掌握的非常熟練了，直接來看代碼。

【代碼實現】

#include <iostream>
#include <cstring>using namespace std;int cnt[10]; // cnt[i] 表示 i 這個數字出現了多少次bool check(int x)
{memset(cnt, 0, sizeof cnt);while(x){cnt[x % 10]++;x /= 10;}if(cnt[0] < 1 || cnt[2] < 2 || cnt[5] < 1) return false; return true;
}int main()
{int c = 0;for(int i = 1; i <= 20250412; i++)if(check(i))c++;cout << c << endl; return 0;
}

題目三：2025圖形

題目鏈接：2025圖形

【題目描述】

【算法原理】

簽到題、模擬、取模運算

找規律 + 周期問題

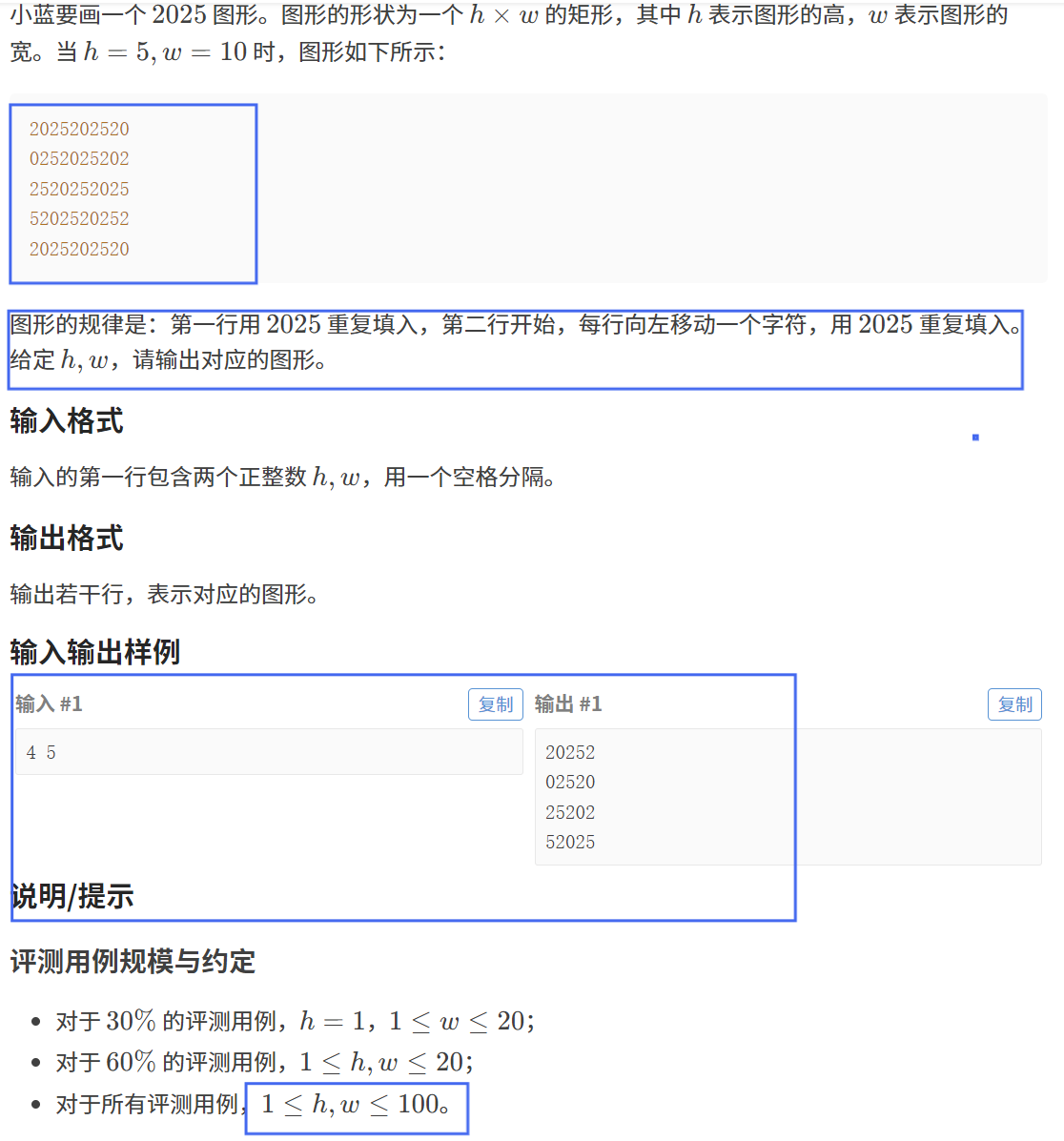
這道題數據范圍很小，我們完全可以首先構造出一個含有 200 個 “2025” 的字符串，然后針對每一行從不同的位置開始輸出 w 個字符就可以了。（代碼可以自己嘗試實現）

但是，這樣玩的話就沒有什么意思了。我們能不能只存一個 “2025” 呢？

我們寫幾行找一找規律：

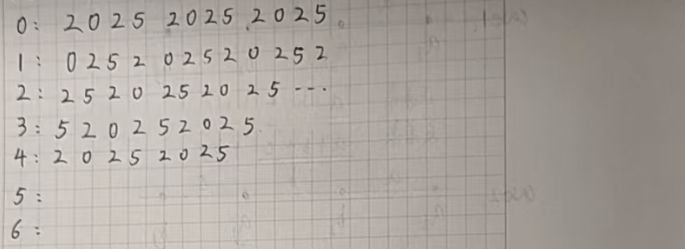
遇到周期問題，我們就要首先想到取模操作。

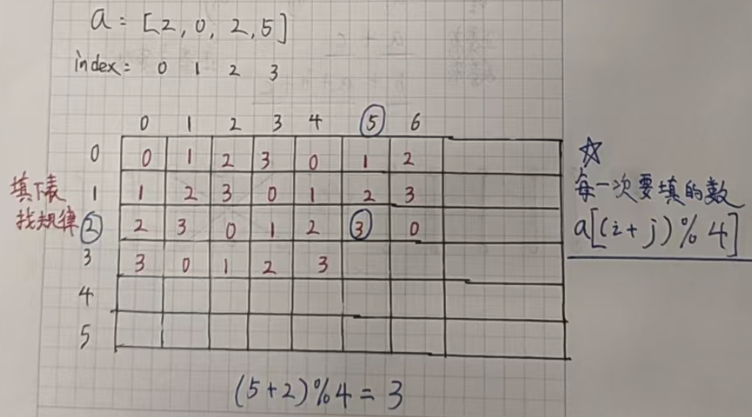
不難發現，這道題輸出位置的值的下標就是橫坐標的值和縱坐標的值之和再模四。

因此，這道題的規律我們就找到了，直接來看代碼：

【代碼實現】

#include <iostream>using namespace std;int a[4] = {2, 0, 2, 5};int main()
{int h, w; cin >> h >> w;for(int i = 0; i < h; i++){for(int j = 0; j < w; j++){cout << a[(i + j) % 4];} cout << endl;}return 0;
}

題目四：最短距離

題目鏈接：最短距離

【題目描述】

【算法原理】

貪心

這道題目一定不要一直拘泥于題目中的那一幅圖當中，我們拋開坐標系不談，其實這道題目就是讓兩個數組中的值一一對應，使得每一組差的絕對值之和最小：

（我當時就盯著題目中的那幅圖在坐標系中想了很長時間）

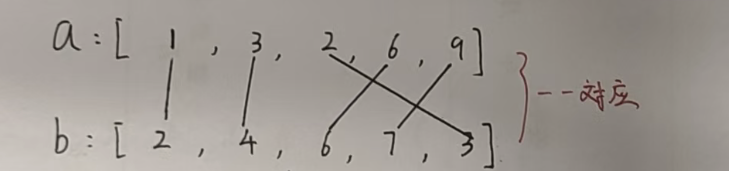
我們很容易想到一個貪心策略，就是將兩個數組排序之后，然后按照從小到大的順序一一對應就可以了。

（大家如果之前接觸過這一類貪心問題的話，貪心策略是很好想出來的。但是如果之前沒接觸過這樣的問題，就把這個貪心策略當成一個經驗積累下來，以后再遇到這樣的問題直接朝這方面想就可以了~~）

（想出貪心策略之后，自己構造幾組測試用例，如果沒有明顯的錯誤的話，直接寫代碼就 OK 了）（由于這里是賽后題解，我接下來會給出詳細證明）。

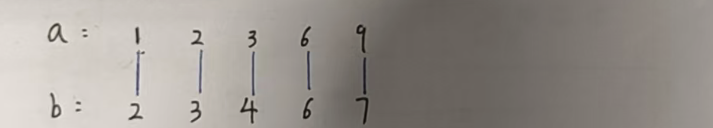
貪心策略的正確性證明：反證法（有興趣的可以看一看下面）

我們假設不是按照下標一位一位對應，只需要證明這樣反著來絕對沒有正著來更優就可以了。

假設 i < j，a[i] <= a[j]，b[i] <= b[j]：

如果正著來的話，我們會讓 a[i] 和 b[i] 對應，a[j] 和 b[j] 對應。

如果反著來的話，我們會讓 a[i] 和 b[j] 對應，a[j] 和 b[i] 對應。

接下來只需要證明在所有的情況下反著來都沒有正著來更優就可以了。

我們根據 a[i] a[j] b[i] b[j] 的位置（大小關系）分情況討論：

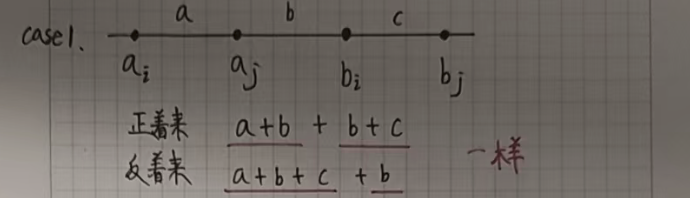
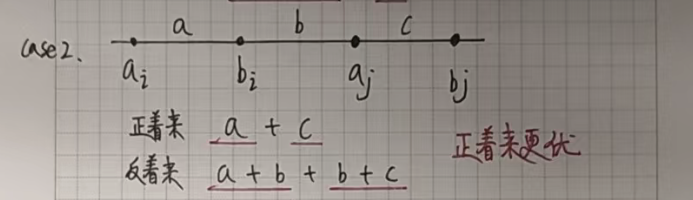
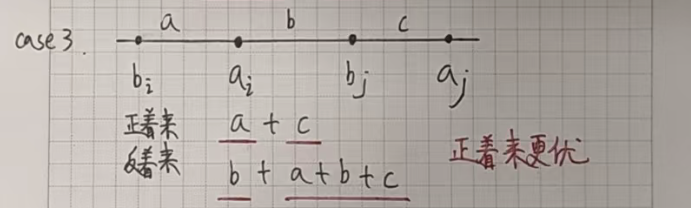
其余情況都類似，就不一一列舉了！！！

【代碼實現】

#include <iostream>
#include <algorithm>
#include <cmath>using namespace std;typedef long long LL;
const int N = 5e4 + 10;int n;
LL a[N], b[N];int main()
{cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n; i++) cin >> b[i];sort(a + 1, a + 1 + n);sort(b + 1, b + 1 + n);LL ret = 0;for(int i = 1; i <= n; i++)	ret += abs(a[i] - b[i]);cout << ret << endl;return 0;
}

題目五：冷熱數據隊列

題目鏈接：冷熱數據隊列

【題目描述】

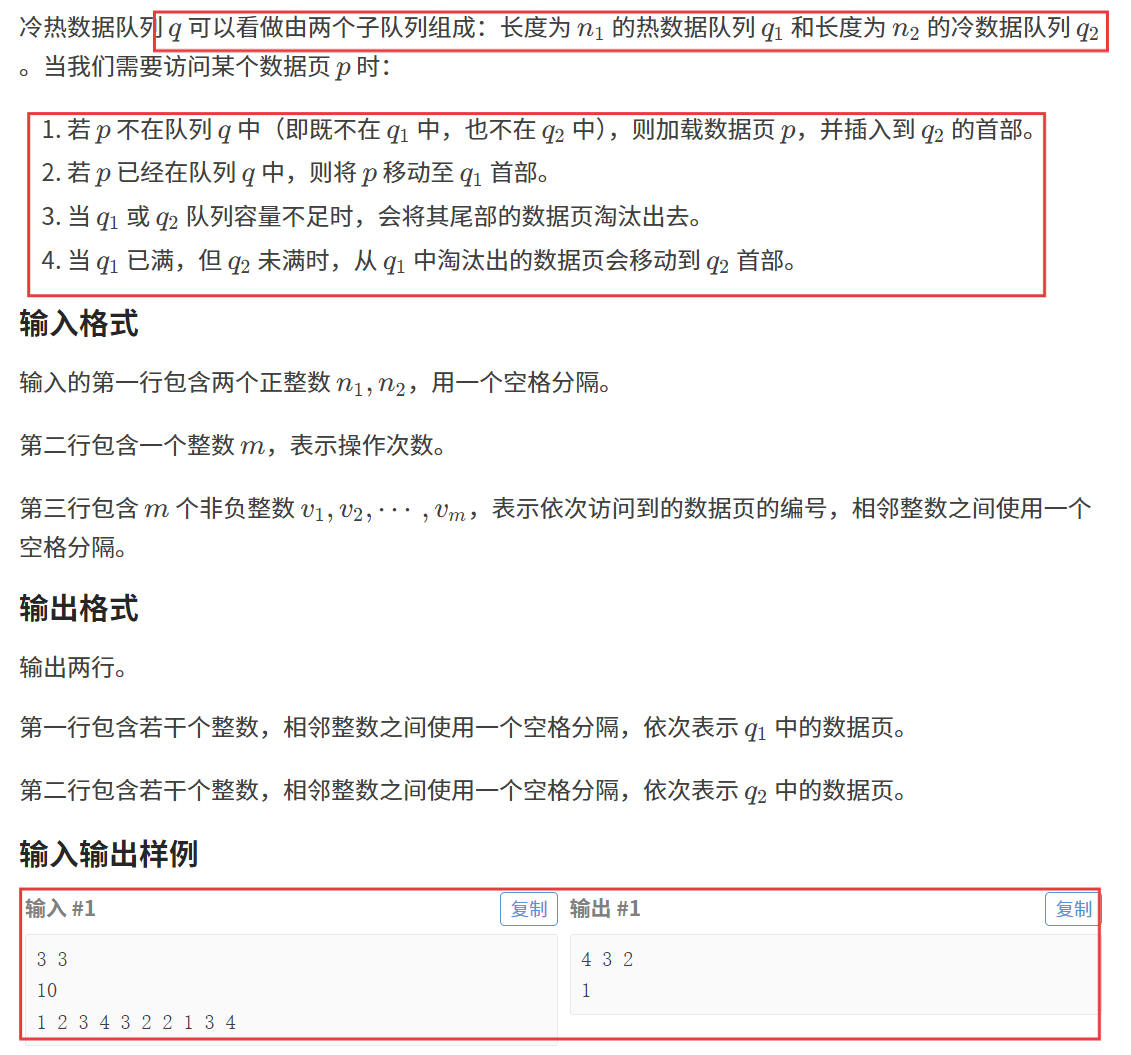
【算法原理】

數據結構 + 模擬

1. 查找：哈希表、紅黑樹；

2. 頭插：鏈表，雙端隊列；

3. 任意位置刪除：雙向鏈表；

4. 尾刪：鏈表，雙端隊列；

由于本題我們需要執行查找操作，因此我們需要哈希表（或紅黑樹）這一數據結構。

我們還需要執行任意位置刪除和頭插操作，因此我們需要雙向鏈表。（STL 中的 List 就行）

執行查找操作要用到的哈希表要能夠配合雙向鏈表的刪除操作，因此我們這樣創建哈希表：

至于 STL 中的 list，我們之前很少使用，這里給大家一些常見的接口：

接下來就是根據題目要求進行模擬的過程了，廢話不多說，直接來看代碼。?

【代碼實現】

#include <iostream>
#include <list>
#include <unordered_map>using namespace std;int n1, n2, m;
list<int> q1, q2;
unordered_map<int, list<int>::iterator> mp1, mp2;int main()
{cin >> n1 >> n2 >> m;while(m--){int x; cin >> x;if(mp1.count(x)){// ?q1.erase(mp1[x]);mp1.erase(x);// ? q1.push_front(x);mp1[x] = q1.begin();}else if(mp2.count(x)){// ?q2.erase(mp2[x]);mp2.erase(x);// ? q1.push_front(x);mp1[x] = q1.begin();}else{q2.push_front(x);mp2[x] = q2.begin();}if(q1.size() > n1){int x = *q1.rbegin();q1.pop_back();mp1.erase(x);q2.push_front(x);mp2[x] = q2.begin();}if(q2.size() > n2){int x = *q2.rbegin();q2.pop_back();mp2.erase(x);}}for(auto x : q1) cout << x << " ";cout << endl;for(auto x : q2) cout << x << " ";cout << endl; return 0;
}

題目六：倒水

題目鏈接：倒水

【題目描述】

【算法原理】

二分答案

這道題目有明顯的二分題眼，要求的是最小值最大是多少。

分析二段性：

我們假設最終答案?ret 表示最小值的最大情況，我們發現如果再大于 ret 的話，是沒有辦法做到的，如果小于 ret 的話，我們是可以做到的。因此本題具有明顯的二段性，我們就可以嘗試使用二分答案來進行解決。

接下來思考如何實現 check 函數？

我們傳入一個值 mid，check 函數的功能是判斷能否通過倒水使得所有瓶子中的最小值大于等于 x，如果能，說明 mid 落在了左區間。如果不能說明 mid 落到了右區間。

我們只需要從前往后遍歷一遍數組，只要該位置的水量大于等于 x，我們就把多余的水往后倒，如果遍歷到某一位置發現水量小于 x，就返回 false，如果全部大于等于 x，就返回 true；

我們直接來看代碼：

【代碼實現】

#include <iostream>
#include <cstring>using namespace std;typedef long long LL;
const int N = 1e5 + 10;LL n, k; 
LL a[N];
LL b[N];bool check(LL x)
{memcpy(b, a, sizeof a);for(int i = 1; i <= n; i++){if(b[i] < x) return false;b[i] -= x;if(i + k <= n) b[i + k] += b[i];} return true;
}int main()
{cin >> n >> k;for(int i = 1; i <= n; i++) cin >> a[i];int l = 0, r = 1e5;while(l < r){int mid = (l + r + 1) >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << l << endl;return 0;
}

題目七：拼好數

題目鏈接：拼好數

【題目描述】

【算法原理】

貪心 + 分類討論

這道題首先大家都可以想到是要統計每一個數中 6 的個數，然后再考慮拼接的問題。

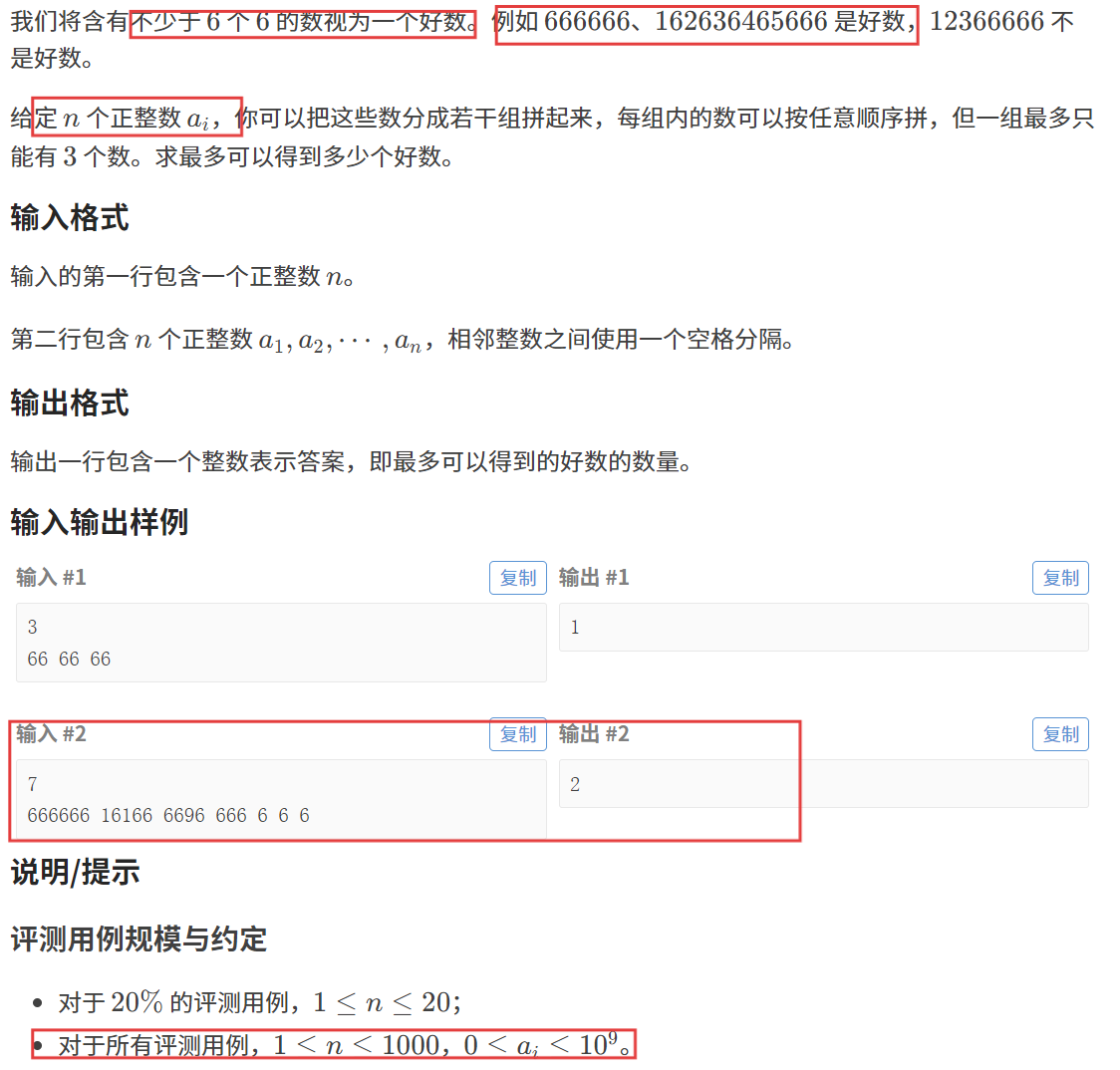
我們預處理出一個 cnt 數組，其中 cnt[i] 表示：出現 6 的次數為 i 時，一共有多少個數。

比如，以第二個測試用例為例，cnt[6] = 1，cnt[3] = 3，cnt[1] = 3；

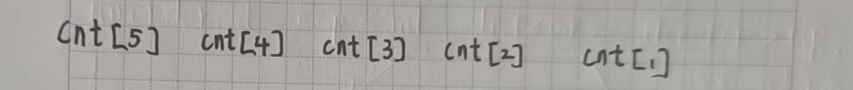
貪心策略：

1. 如果一個數 6 的出現次數大于等于 6，直接讓 ret + 1 即可，這個數可以單獨成為一個小組。

2. 如果能用 1 去湊，就盡量先使用 1 去湊；因為1 不能單獨湊成 6，只能和別的數配合使用。

? ? 能用 1 就先用 1，這樣就可以把其余更有用的數保留下來，去湊更多的可能性。

3. 在第二點的基礎上，如果能用更少的數湊成，就不用更多的數。

4. 在前面幾點的基礎上，優先用更容易湊出 6 的數去拼湊。?

直觀感受一下，這個貪心策略肯定是正確的~~~

那我們就確定了各種拼湊方式的優先級：

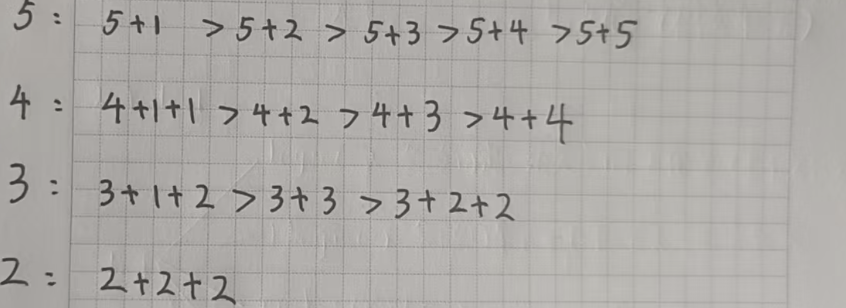
然后我們就可以去寫代碼了，廢話不多說，直接來看代碼：

【代碼實現】

#include <iostream>using namespace std;const int N = 10;int n;
int cnt[N];// 統計 6 出現的次數 
int calc(int x)
{int c = 0;while(x){if(x % 10 == 6) c++;x /= 10;}return c;
}int main()
{cin >> n;int ret = 0;for(int i = 1; i <= n; i++){int x; cin >> x;int t = calc(x);if(t >= 6) ret++;else cnt[t]++;}// 分類討論if(cnt[5]){// 5 + 1  5 + 2  5 + 3  5 + 4 for(int i = 1; i <= 4 && cnt[5]; i++){// cnt[i] + cnt[5]if(cnt[5] <= cnt[i]){ret += cnt[5];cnt[i] -= cnt[5];cnt[5] = 0;} else{ret += cnt[i];cnt[5] -= cnt[i];cnt[i] = 0;}} ret += cnt[5] / 2;} if(cnt[4]){// 4 + 1 + 1if(cnt[4] * 2 <= cnt[1]){ret += cnt[4];cnt[1] -= cnt[4] * 2;cnt[4] = 0; } else{ret += cnt[1] / 2;cnt[4] -= cnt[1] / 2;cnt[1] %= 2;}// 4 + 2  4 + 3for(int i = 2; i <= 3 && cnt[4]; i++){// cnt[i] + cnt[4]if(cnt[4] < cnt[i]){ret += cnt[4];cnt[i] -= cnt[4];cnt[4] = 0;} else{ret += cnt[i];cnt[4] -= cnt[i];cnt[i] = 0;}} // 4 + 4ret += cnt[4] / 2;} if(cnt[3]){// 3 + 1 + 2if(cnt[1] && cnt[2]){int t = min(min(cnt[1], cnt[2]), cnt[3]);ret += t;cnt[1] -= t;cnt[2] -= t;cnt[3] -= t;}// 3 + 3ret += cnt[3] / 2;cnt[3] %= 2;// 3 + 2 + 2 -> 2 + 2 + 2 cnt[2] += cnt[3]; }ret += cnt[2] / 3;cout << ret << endl;return 0;
}

題目八：登山

題目鏈接：登山

【題目描述】

【算法原理】

本場比賽的壓軸題目、逆序對、圖論、并查集、單調棧

首先我們要模擬一下輸入輸出樣例，弄明白題目讓我們做什么。

這道題目從起點的行走方式如下：

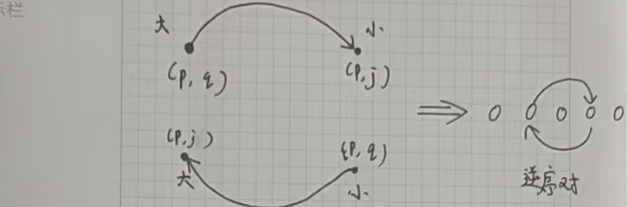
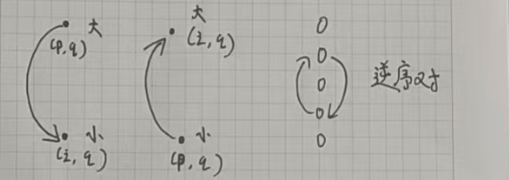
我們先不要考慮二維，可以發現：無論橫著看還是豎著看，只要是構成逆序對的話，就有雙向邊。

那么這道題目就可以轉化成一個圖論問題：

由于二維坐標不好處理，我們先把二維坐標轉化成一維坐標：

根據逆序對建圖之后，我們只需要統計每一個連通塊（并查集）的最大值，再把所有的點遍歷一遍，判斷它是在哪一個連通塊，直接累加上這個最大值就可以了。

接下來考慮下一個問題：如何把這個圖給建出來呢？？？

肯定不能直接把所有的逆序對都連上雙向邊，因為時間和空間都不允許。（共 nmm + mnn 條邊）

但是我們發現，圖是沒有必要完全建出來的，我們僅需搞定并查集能夠找到連通塊中的最大值就可以了。

因此，我們這樣來處理這個問題：（當成經驗積累下來）

我們從前往后遍歷數組，如果該元素比前一個位置小，就一直往前合并并查集，順便刪除合并過的元素，直到該元素比前面的元素大。再把該元素存儲起來。

類似單調棧的過程，我們用棧來模擬這個過程。

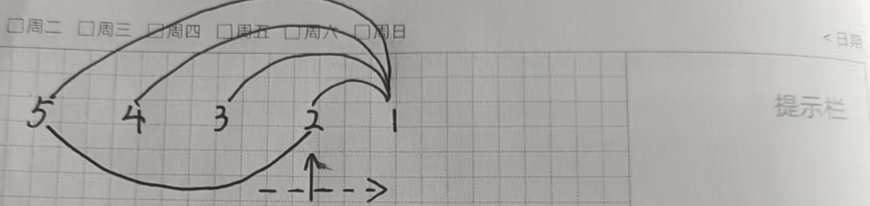
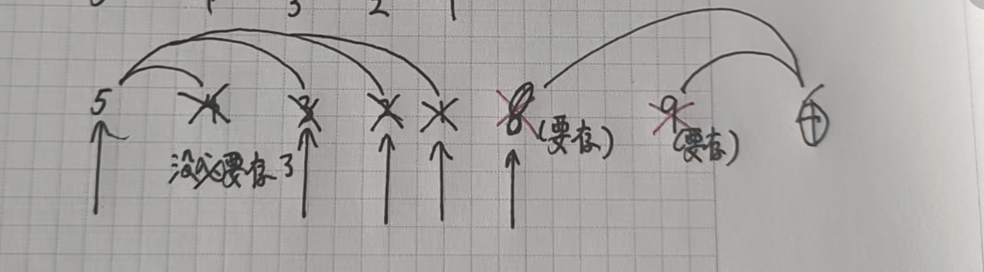
我們直接來看代碼：

【代碼實現】

#include <iostream>using namespace std;const int N = 1e6 + 10;int n, m;
int a[N];
int fa[N]; // 并查集
int st[N], top; // 棧// 二維轉一維
int get_id(int i, int j)
{return i * m + j;
} int find(int x)
{return fa[x] == x ? x : fa[x] = find(fa[x]);
}void merge(int x, int y)
{x = find(x), y = find(y);if(x == y) return;// 小的合并到大的 if(a[x] >= a[y]) fa[y] = x;else fa[x] = y;
}int main() 
{cin >> n >> m;for(int i = 1; i < n * m; i++) fa[i] = i;for(int i = 0; i < n; i++)for(int j = 0; j < m; j++)cin >> a[get_id(i, j)];// 建圖for(int i = 0; i < n; i++){top = 0;for(int j = 0; j < m; j++){int t = top, id = get_id(i, j);while(top && a[st[top]] > a[id]){merge(st[top], id);top--;}if(t == top) st[++top] = id;else st[++top] = st[t];}} for(int j = 0; j < m; j++){top = 0;for(int i = 0; i < n; i++){int t = top, id = get_id(i, j);while(top && a[st[top]] > a[id]){merge(st[top], id);top--;}if(t == top) st[++top] = id;else st[++top] = st[t];}} double ret = 0;for(int i = 0; i < n * m; i++) ret += a[find(i)];printf("%.6lf\n", ret / (n * m));return 0;
}

好了，本期的內容就到這里了。期待我們下次見面。