---

---

一、二叉搜索樹（排序樹）

1. 概念初識

我們二叉搜索樹有以下幾個特點，即

1. 左子樹不為空時，左子樹節點值都小于根節點的值
2. 右子樹不為空時，右子樹節點值都大于根節點的值
3. 并且對于左右子樹來看，其子樹也是滿足這兩個條件

當我們對這個二叉搜索樹進行中序遍歷后，得到的就是一個有序的值的集合
以下是這種搜索樹的示例

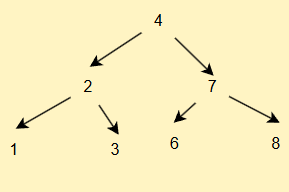
我們進行中序遍歷后得到的結果是1 2 3 4 6 7 8

好，當我們插入節點的時候，就不需要去遍歷全部的節點了
如果我們插入的節點它的值大于根節點，說明要去右邊插入，否則就是左邊
比如我想插入9這個節點，直接去根節點為8的右樹 插入即可 `
這樣就提高了插入效率，類似于“二分”

但是你是否想過一種極端情況，它因為所有節點都是升序的，會變成一顆單分支的樹，1-->2-->3，這樣就會退化成n的時間復雜度

因此我們定義的二叉搜索樹，左右樹的高度不能超過1
對于1-->2-->3也不是沒有解決辦法，我們可以把其進行旋轉，這樣就可以變成
2
/ \
1 3
有很多種旋轉，比如左旋，右旋，或者是雙旋，我們熟知的紅黑樹就是旋轉得來的，再加上顏色的標記

2. 模擬實現

1. 創建搜索樹節點

static class TreeNode{public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;

2. 查找指定元素是否存在

//查找方法public boolean search(int val){if(root == null){return false;}TreeNode current = root;while(current != null){if(current.val < val){current = current.right;}else if(current.val > val){current = current.left;}else{return true;}}return false;}

3. 插入

我們通過之前的概念演示不難看出，我們插入的節點一般都是在葉子節點插入的

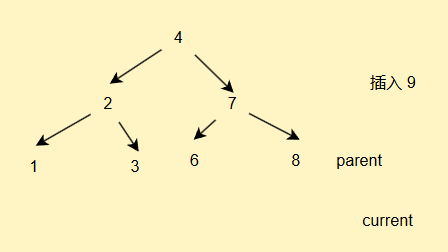
//插入方法public void insert(int val){if(root == null){//說明根節點就是我們的新節點root = new TreeNode(val);return;}//我們插入節點要定義一個雙親節點保存信息//因為我們最后current會走到空的位置，//循環不好出來，此時不好連接TreeNode current = root;TreeNode parent = null;while(current != null){if(current.val > val){parent = current;current = current.left;}else if(current.val < val){parent = current;current = current.right;}else{//重復的值我們不進行存儲return;}}TreeNode newNode = new TreeNode(val);//為什么不用判斷等于，因為等于的情況我們前面已經return走了if(parent.val > val){parent.left = newNode;}else{parent.right = newNode;}}

4. 刪除

這個有點難度，我們得分情況討論

如果current.left == null

1. 如果current == root，直接root = cur.right
   
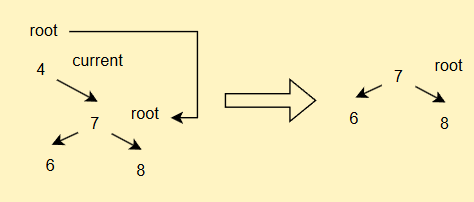
2. 如果current不為root，但是其為parent的左子樹
   
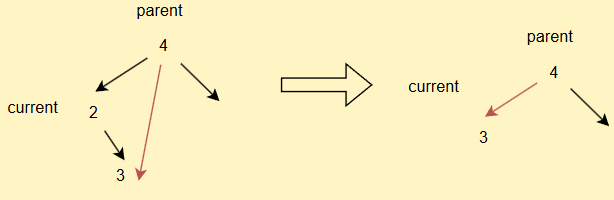
3. 如果current不為root，但是其為parent的右子樹
   

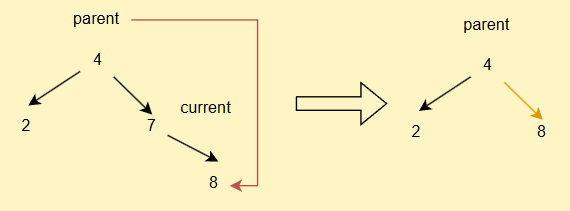
同理，如果current.right == null

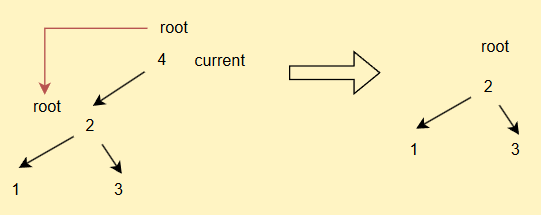
1. 如果current == root，直接root = current.left
   
2. 如果current不為root，但是其為parent的左子樹，直接parent.left = current.left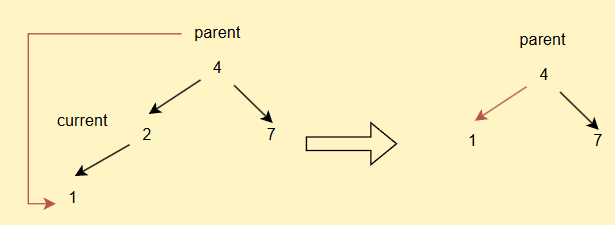
3. 如果current不為root，但是其為parent的右子樹，直接parent.right = current.left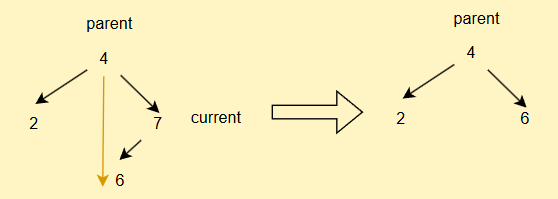

現在，我們處理最棘手的一種情況，即current.left != null && current.left != null
我們要使用替換的思想，而不是真的把目標節點刪除，因為我們要保證刪除后新的節點的左樹小于當前節點值，右樹大于當前節點值
因此我們要在右樹的左子樹搜索最小值，放在當前要刪除的節點的位置（或者在左樹的右子樹中搜尋最大值放在要刪除的節點的位置）
因此我們還需要兩個遍歷，一個是找到最大值的節點的引用target，一個是找到最大值的節點其雙親節點的引用targetParent

//刪除方法public void remove(int val) {TreeNode current = root;TreeNode parent = null;while (current != null) {if (current.val > val){parent = current;current = current.left;}else if(current.val < val){parent = current;current = current.right;}else{removeNode(current,parent);return;}}}private void removeNode(TreeNode current,TreeNode parent) {if (current.left == null) {if (current == root) {root = current.right;} else if (current == parent.left) {parent.left = current.right;} else if (current == parent.right) {parent.right = current.right;}} else if (current.right == null) {if (current == root) {root = current.left;} else if (current == parent.left) {parent.left = current.left;} else if (current == parent.right) {parent.right = current.left;}}else{TreeNode target = current;TreeNode targetParent = null;//尋找左樹中的最小值while(target.left != null){targetParent = target;target = target.left;}current.val = target.val;targetParent.left = target.right;}}

但是我想告訴你，這段代碼有個小錯誤，在這里

TreeNode target = current;
TreeNode targetParent = null;
//尋找左樹中的最小值
while(target.left != null){targetParent = target;target = target.left;
}
current.val = target.val;
targetParent.left = target.right;

為什么？你看，如果我們遇到這種情況

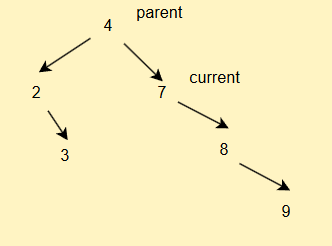
此時targetParent.left = target.right會導致節點錯放的問題

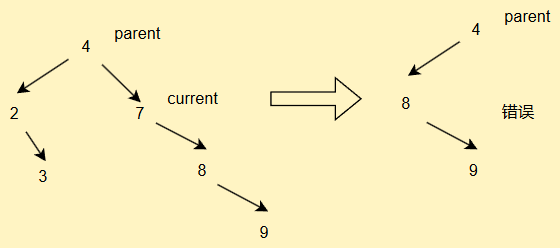
因此要加以判斷

if(target == targetParent.right) {targetParent.right = target.right;
}else{targetParent.left = target.right;
}

自定義一個測試類Test

public static void main(String[] args) {TreeNodeTest treeNodeTest = new TreeNodeTest();//創建節點，插入值int [] test = new int[10];for (int i = 0; i < test.length; i++) {test[i] += 2*i;}for(int x:test){treeNodeTest.insert(x);}//查詢值是否存在System.out.println(treeNodeTest.search(10));//刪除值treeNodeTest.remove(10);//查詢值是否存在System.out.println(treeNodeTest.search(10));}

二、Map類

Map類它是一個獨立的接口，不繼承Collection類，我們之前右講過哈希表，內部具有映射關系
我們現在就以單詞String和這個單詞出現的頻次Integer來探究這種映射關系
我們新建一個類Map<String,Integer> map = new TreeMap<>();
我們TreeMap其底層就是一個二叉搜索樹，HashMap我們之后再講

我們講幾個常用的方法，以我們剛剛的單詞例子

1. put——設置單詞以及其頻次

map.put("zlh",5);
map.put("hello",1);
map.put("hi",3);

2. get——獲取單詞頻次

System.out.println(map.get("zlh"));//5
System.out.println(map.get("hello"));//1

3. getOrDefault——獲取單詞頻次或返回默認值

這個方法就是如果我們獲取的單詞不存在，就返回默認值，默認值可以自己設定

System.out.println(map.getOrDefault("hi",999));//3
System.out.println(map.getOrDefault("lll",6666));//6666

4. remove——刪除單詞頻次信息

map.remove("hi");
System.out.println(map.getOrDefault("hi",1111));//1111

5. keySet——取出單詞放入大集合Set中

這個大集合Set因為不能有重復元素，因此可以有去重效果

Set<String> set;
set = map.keySet();
System.out.println(set);//[hello, zlh]

6. values——取出對應單詞頻次放入Collection中

這個Collection可以有重復元素，而且這個是一個數集

map.put("cheerful",5);
Collection<Integer> collection;
collection = map.values();
System.out.println(collection);//[5, 1, 5]

7. containsKey——查看單詞是否存在

System.out.println(map.containsKey("zlh"));//true

8. containsValue——查看頻次是否存在

System.out.println(map.containsValue(999999));//false

9. entrySet——返回所有的映射關系

Set<Map.Entry<String,Integer>> sets = map.entrySet();
for(Map.Entry<String,Integer> es : sets){//強遍歷String str = es.getKey();System.out.print(str+" ");Integer val = es.getValue();System.out.println(val+" ");
}

10. 注意事項

1. 就跟哈希表一樣的，單詞不可以重復，頻次可以重復
2. 單詞不可以是空的單詞map.put(null,5)，因為底層誰白了也是一顆樹，樹連節點引用都沒有，談何賦值
3. Map中的Key和Value根據剛剛到演示，看到是可以分離出的

三、Set類

因為Set類繼承了Collection類，并且是一個數集，因此只可以存入Value

Set<Integer> set = new TreeSet<>();

我們隨便舉幾個例子，說明其內部的方法

1. add——添加元素

我們是不可以添加重復元素的

set.add(11);

2. contains、clear、remove、size、isEmpty、toArray

分別是檢測是否存在，清空，刪除，求大小，檢測是否是空的，轉換成數組

System.out.println(set.contains(11));//true
set.remove(11);
System.out.println(set.size());//1
System.out.println(set.isEmpty());//false
System.out.println(Arrays.toString(set.toArray()));//[999]
set.clear();
System.out.println(set.isEmpty());//true

我們點開TreeSet的源碼，發現其底層實現的是TreeMap，這樣就保證了集合的數據唯一性

我們不光可以new TreeSet，還可以new LinkedList，這是一個雙向鏈表的集合

四、哈希表（又稱散列表）

1. 哈希沖突

我們在放入元素的時候，一般是要去尋找其位置放哪，但是如果我定義一個哈希表長度為10，下標從0~9
那我放入兩個元素2和12，我們根據%10求的結果都要放入1下標，此時沖突就產生了

2. 避免哈希沖突

1. 設計哈希函數

我們運用的是除留余數法，即*表中地址數為m，取出一個不大于m的最接近或者是等于m的質數作為除數p，則公式$Hash(Key) = key % p，講計算結果的關鍵碼轉為哈希地址
還有String類中的hashCode方法解決字符串沖突以及Integer中的hashCode方法解決數值沖突

2. 直接定制

我們通常需要設計一個合理的哈希函數，還記得我們之前經常使用的模擬哈希表嗎，比如統計字符出現次數
而我們都是-='a'去計算偏移量的

3. 調整負載因子

舉個例子，如果是數組，我們就進行擴容操作

3. 解決哈希沖突

1. 閉散列

一般在發生哈希沖突的時候，哈希表是沒有滿的，因此其必定是有空位置的，我們可以把沖突Key值放入其下一個空的位置中去
每次放的時候，我們都探測一下，這個探測是線性的

但是這樣放那面太集中了，容易把沖突的元素放在一塊，因此我們給出個優化方法
Hi = (H0+i^2)%m，i代表第幾次放入，H0代表第一次放入的位置（不沖突時候），m代表這個表的長度

因此，閉散列無需額外空間就可以刪除，而且結果存儲是連續的，而且不需要指針去引用
但是，盡管有剛剛的優化方法，還是會導致沖突元素的聚集，而且刪除有一個很麻煩的事情
就比如我們剛剛到表，假設我們把2刪除后，誰去下標2的位置，而且我們也不知道下標2的元素刪沒刪
因此我們要在各個下標定義標記，為0和1，但是這樣繼續進來元素，又會導致二次聚集，因此閉散列不可靠，也很不效率

2. 開散列（又稱散列桶/哈希桶）

我們采用大小集合結合的方式，我們每一個下標都存入一個小集合，形成映射關系
沖突的元素全部都放入小集合中，如果小集合內部沖突元素太多，我們就把其轉換成搜索樹或者是哈希函數的再設計

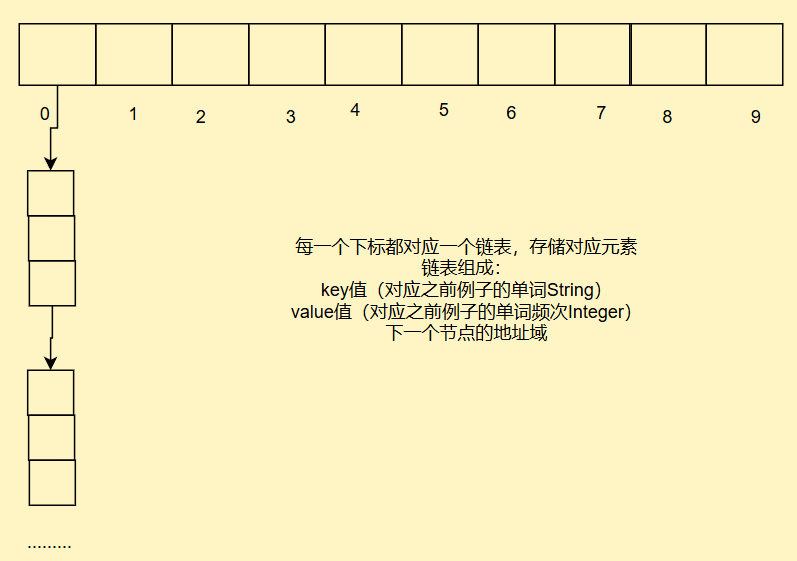
自定義一個類MapAndSetTest實現模擬表

static class Node{public int key;//對應之前例子中單詞Stringpublic int val;//對應之前例子中單詞頻次Integerpublic Node next;//下一節點的地址域public Node(int key, int val) {this.key = key;this.val = val;}}public Node[] array;//表數組public int usedSize;//有效元素個數，用來計算負載因子public double load = 0.75;//默認負載因子大小public MapAndSetTest(){//建立表array = new Node[10];}

1. 插入元素
   如果數組滿了要擴容，但是我們不能就簡單的擴容，我們擴容之后，原本沖突的值我們要重新規劃其放的位置
   比如原本大小為10下標0~9的這個表中，在下標2存放了2,12
   擴容后到了大小為20下標0~19，因此我們要把下標2中的12存入下標12

因此說白了就是擴容后要把表中所有下標的所有元素重新遍歷放入新的下標中

//加入元素public void put(int key,int val){//先找到下標位置//找到位置后看看是否和已有的key值重復//不重復的話就采用頭插法（尾插也可以）int index = key % array.length;Node current = array[index];while(current != null){if(current.key == key){//如果出現重復的key值，我們就更新內部的value就好current.val = val;}current = current.next;}//說明不存在key值，執行頭插操作Node insertNode = new Node(key,val);insertNode.next = array[index];array[index] = insertNode;this.usedSize++;//插入后檢查負載因子，如果超過限定額度要進行擴容if(isFull() >= load){//擴容grow();}}private double isFull(){return usedSize*1.0/array.length;//*1.0是為了轉換成小數計算}private void grow() {//此時我們先創造一個空的表Node [] newArray = new Node[array.length*2];//遍歷原表中的所有下標的所有元素for (int i = 0; i < array.length; i++) {Node current = array[i];while(current != null){int newIndex = current.key% newArray.length;//采用頭插法在新的表中的對應下標插入元素//為了防止頭茬后我們的current跑到別的下標的鏈表中去//因此我們要實現保存當前下標的后續鏈表的信息Node nextCurrent = current.next;current.next = newArray[newIndex];newArray[newIndex] = current;current = nextCurrent;}}//更新表this.array = newArray;}

2. 獲取對應key值的value

//獲取對應的key值的valuepublic int get(int key){int index = key%array.length;Node current = array[index];while(current != null){if(current.key == key){return current.val;}current = current.next;}return -1;}

3. 測試

public static void main(String[] args) {MapAndSetTest mapAndSetTest = new MapAndSetTest();int[] test = new int[5];Random random = new Random();for (int i = 0; i < test.length; i++) {test[i] = random.nextInt(25);}for (int x : test) {mapAndSetTest.put(x, x / 2);}//查看結果for (int i = 0; i < mapAndSetTest.array.length; i++) {Node current = mapAndSetTest.array[i];if (current != null) {System.out.print("Bucket " + i + ": ");while (current != null) {System.out.print("(" + current.key + "," + current.val + ") ");current = current.next;}System.out.println();}}//獲取對應key值元素System.out.println(mapAndSetTest.get(22));}

---

文章錯誤不可避免，期待您的指正，我們共同進步

---

---

END