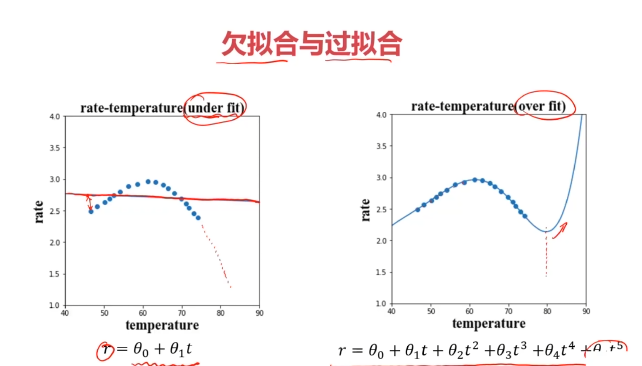
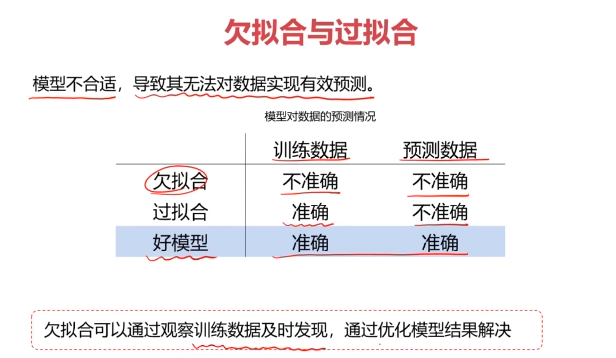
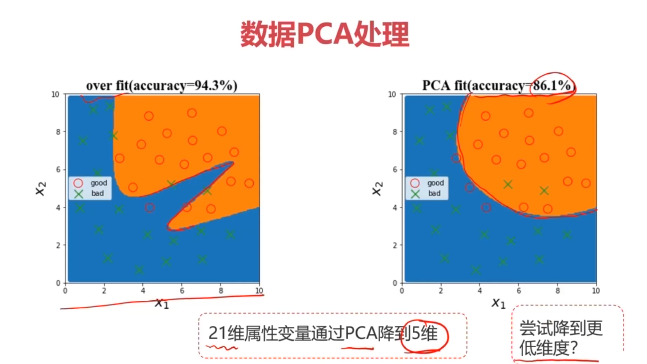
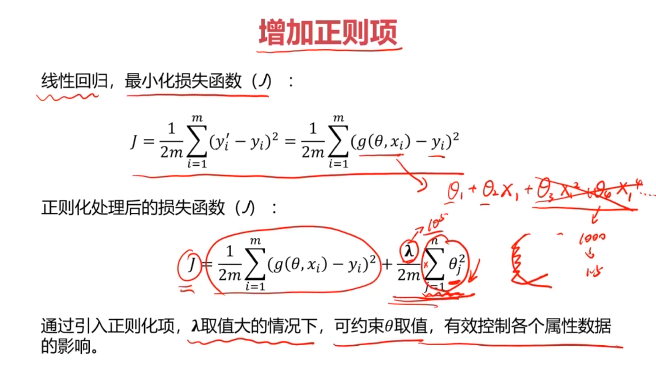
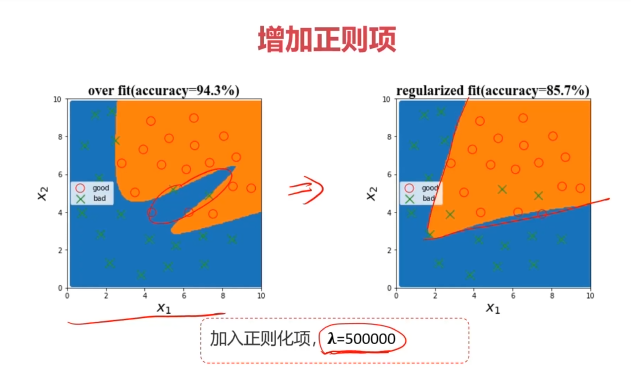
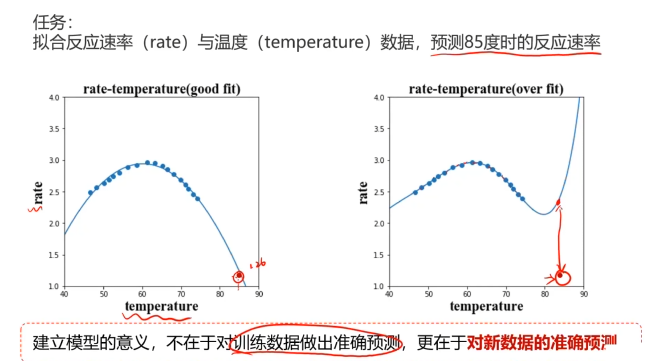
一、欠擬合與過擬合


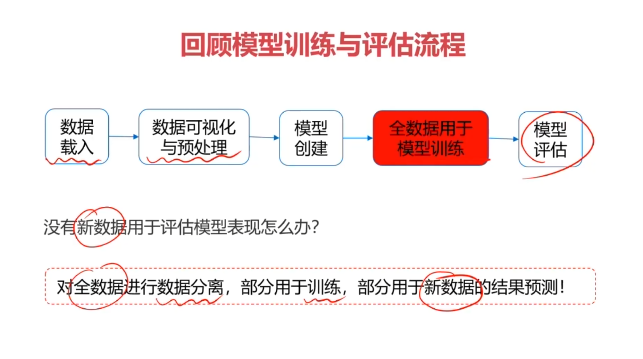
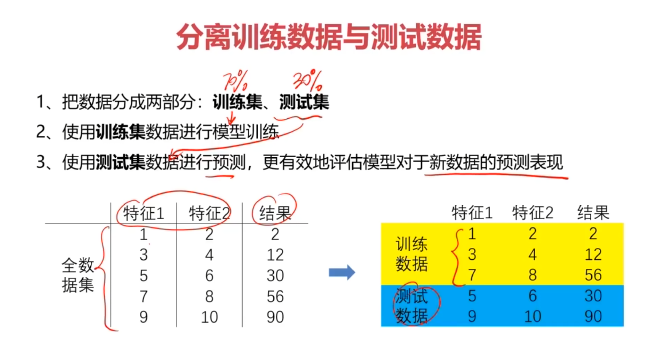
二、數據分離與混淆矩陣
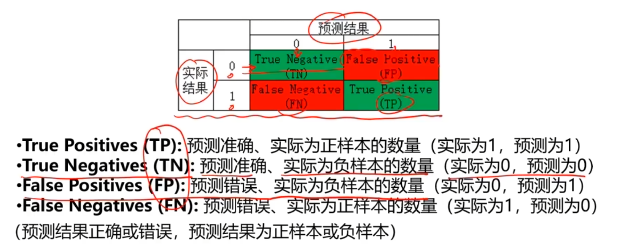
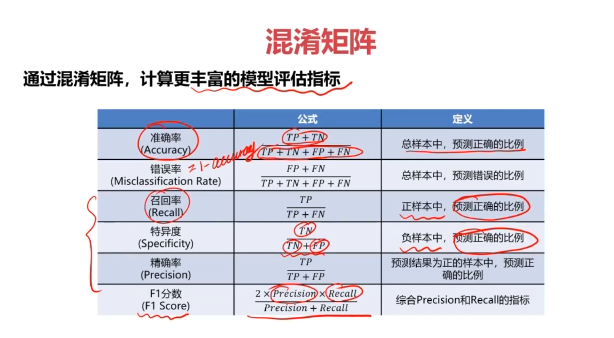
混淆矩陣(Confusion Matrix)
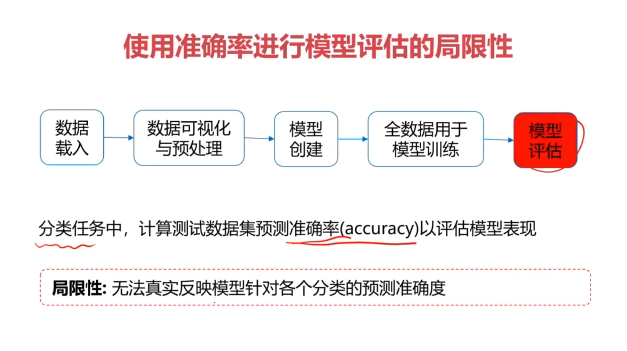
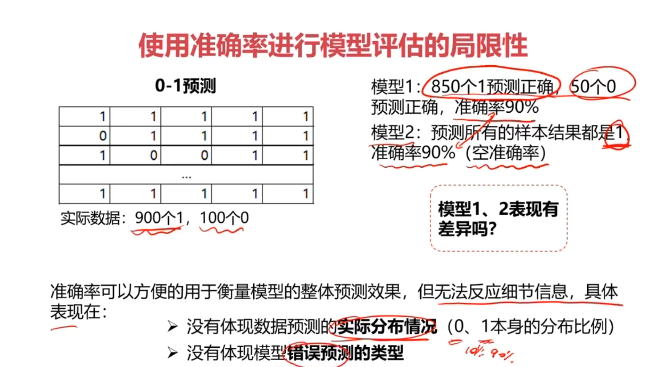
混淆矩陣,又稱為誤差矩陣,用于衡量分類算法的準確程度
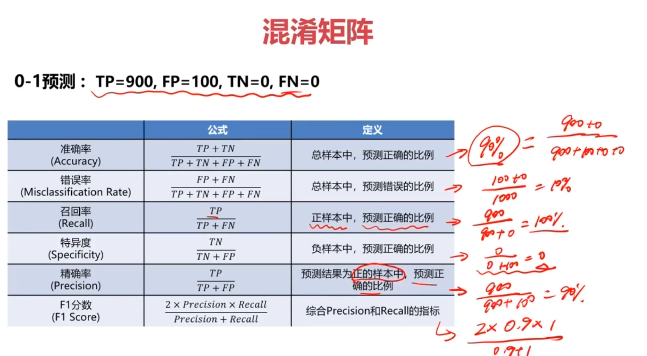

二、模型優化



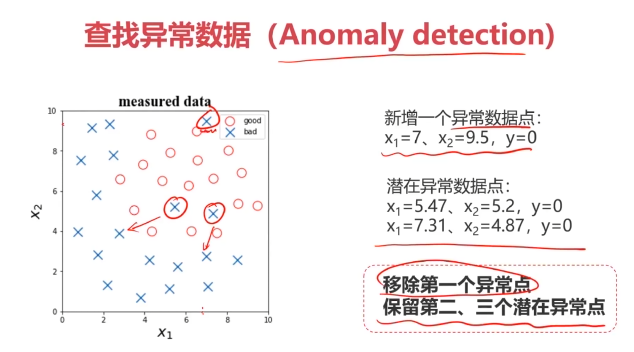
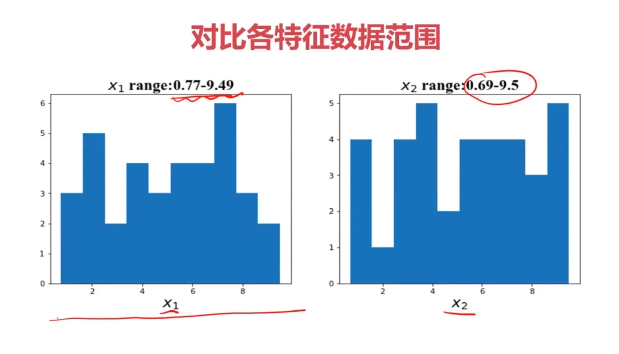
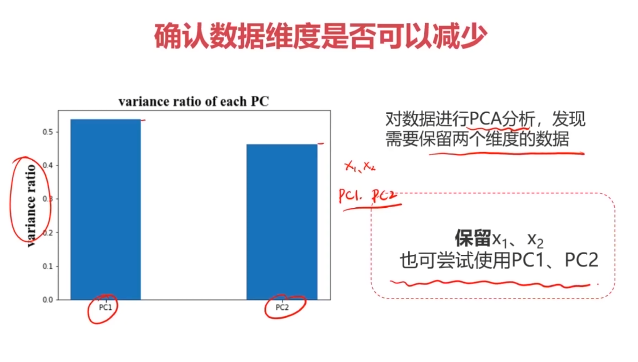
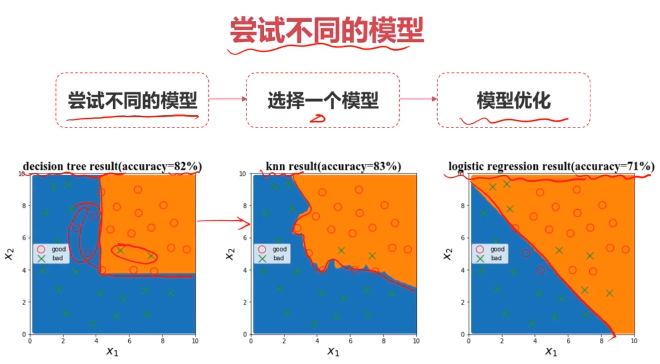

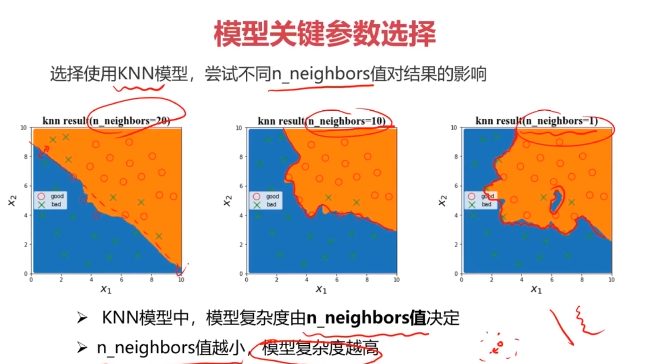
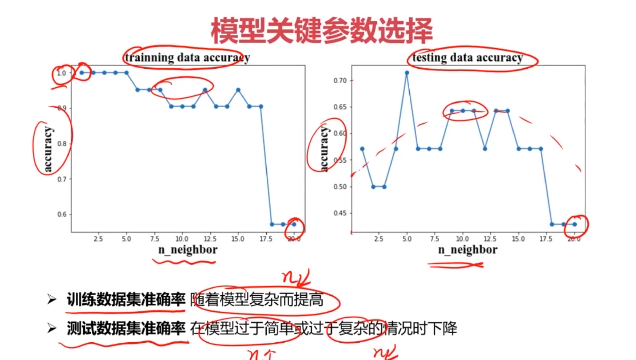
四、實戰準備
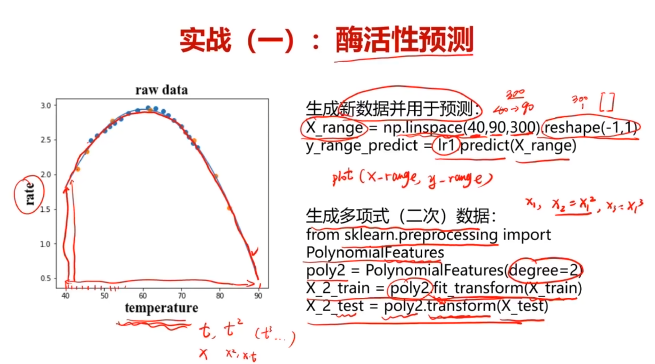
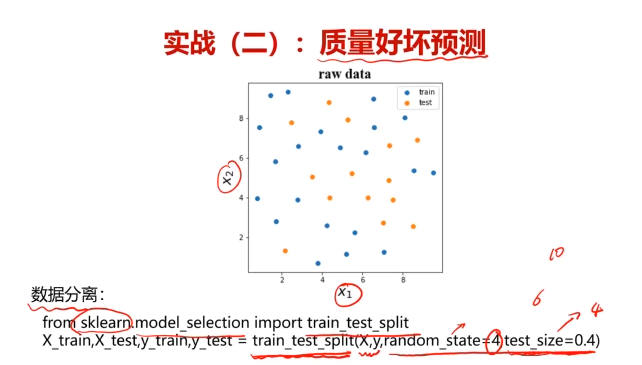
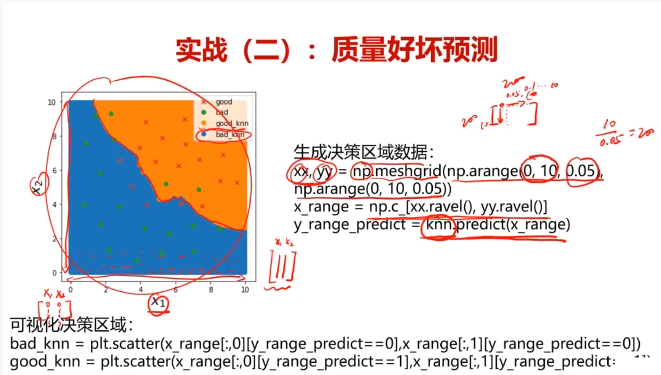

五、酶活性預測,使用數據集T-R-train.csv,測試集T-R-test.csv
#加載數據
import pandas as pd
import numpy as np
data_train = pd.read_csv('T-R-train.csv')
data_train.head()
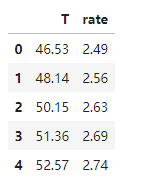
data_test = pd.read_csv('T-R-test.csv')
data_test.head()
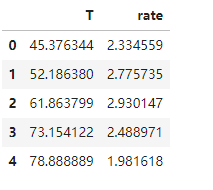
#賦值x,y
x_train = data_train.loc[:,'T']
y_train = data_train.loc[:,'rate']x_test = data_test.loc[:,'T']
y_test = data_test.loc[:,'rate']
#可視化數據
from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.scatter(x_train,y_train)
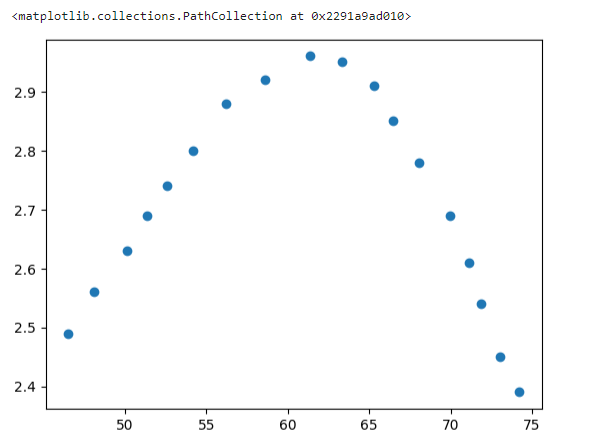
#轉換成一維數組
x_train = np.array(x_train).reshape(-1,1)
x_test = np.array(x_test).reshape(-1,1)
print(x_train.shape,x_test.shape)
#創建線性回歸模型
from sklearn.linear_model import LinearRegression
lr1 = LinearRegression()
lr1.fit(x_train,y_train)
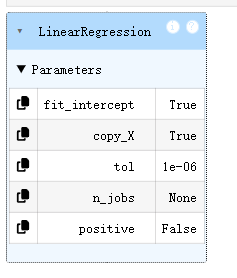
#預測數據
y_train_predict = lr1.predict(x_train)
y_test_predict = lr1.predict(x_test)#計算R二分數,越接近1,說明模型越好
from sklearn.metrics import r2_score
r2_train = r2_score(y_train,y_train_predict)
r2_test = r2_score(y_test,y_test_predict)
print(r2_train,r2_test)
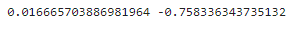
#可視化模型預測結果
x_range = np.linspace(40,90,300).reshape(-1,1)
y_range_predict = lr1.predict(x_range)
fig2 = plt.figure()
plt.plot(x_range,y_range_predict)
plt.scatter(x_train,y_train)
plt.title('prediction data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
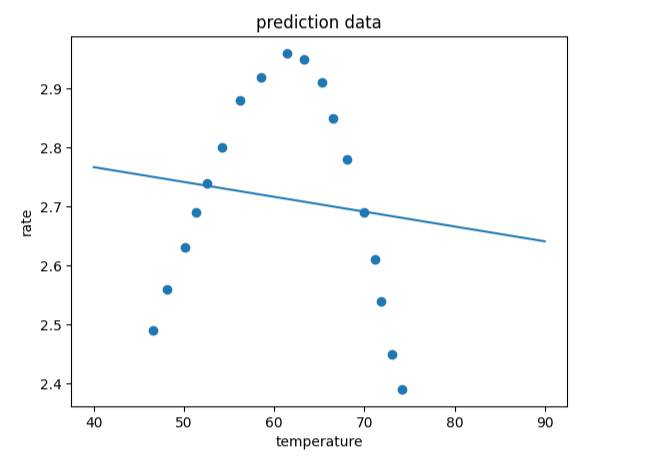
#多項式模型
from sklearn.preprocessing import PolynomialFeatures
poly2 = PolynomialFeatures(degree=2)
x_2_train = poly2.fit_transform(x_train)
x_2_test = poly2.transform(x_test)
print(x_2_train)

lr2 = LinearRegression()
lr2.fit(x_2_train,y_train)#預測數據
y_2_train_predict = lr2.predict(x_2_train)
y_2_test_predict = lr2.predict(x_2_test)#計算R二分數,越接近1,說明模型越好
from sklearn.metrics import r2_score
r2_2_train = r2_score(y_train,y_2_train_predict)
r2_2_test = r2_score(y_test,y_2_test_predict)
print(r2_2_train,r2_2_test)

#可視化模型預測結果
x_2_range = np.linspace(40,90,300).reshape(-1,1)
x_2_range_p = poly2.transform(x_2_range)
y_2_range_predict = lr2.predict(x_2_range_p)
print(x_2_range,y_2_range_predict)
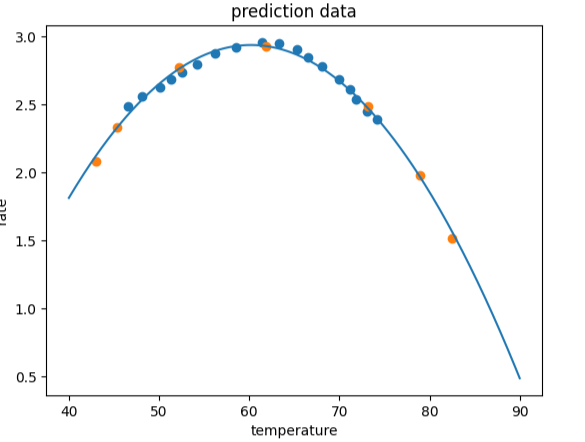
fig4 = plt.figure()
plt.plot(x_2_range,y_2_range_predict)
plt.scatter(x_train,y_train)
plt.scatter(x_test,y_test)
plt.title('prediction data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
poly5 = PolynomialFeatures(degree=5)
x_5_train = poly5.fit_transform(x_train)
x_5_test = poly5.transform(x_test)
print(x_5_train.shape,x_5_train)

lr5 = LinearRegression()
lr5.fit(x_5_train,y_train)#預測數據
y_5_train_predict = lr5.predict(x_5_train)
y_5_test_predict = lr5.predict(x_5_test)#計算R二分數,越接近1,說明模型越好
from sklearn.metrics import r2_score
r2_5_train = r2_score(y_train,y_5_train_predict)
r2_5_test = r2_score(y_test,y_5_test_predict)
print(r2_5_train,r2_5_test)
#可視化模型預測結果
x_5_range = np.linspace(40,90,300).reshape(-1,1)
x_5_range_p = poly5.transform(x_5_range)
y_5_range_predict = lr5.predict(x_5_range_p)
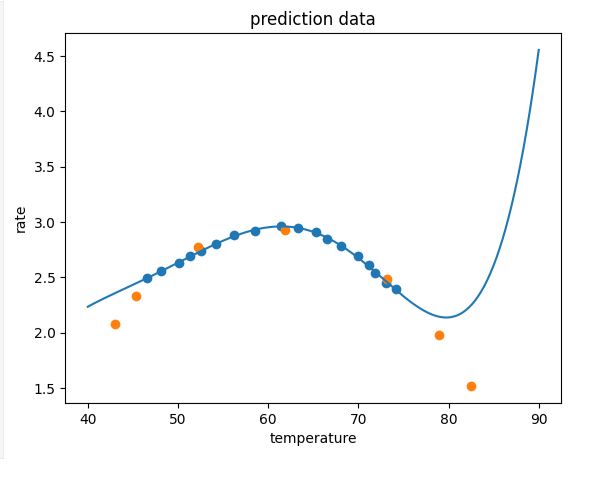
# print(x_5_range,y_5_range_predict)fig4 = plt.figure()
plt.plot(x_5_range,y_5_range_predict)
plt.scatter(x_train,y_train)
plt.scatter(x_test,y_test)
plt.title('prediction data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
六、芯片質量好壞分類任務,使用數據集data_class_raw.csv
#加載數據
import pandas as pd
import numpy as np
data = pd.read_csv('data_class_raw.csv')
data.head()
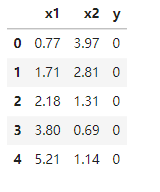
#賦值x,y
x = data.drop(['y'],axis=1)
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']
y = data.loc[:,'y']
#可視化數據
from matplotlib import pyplot as plt
fig1 = plt.figure()
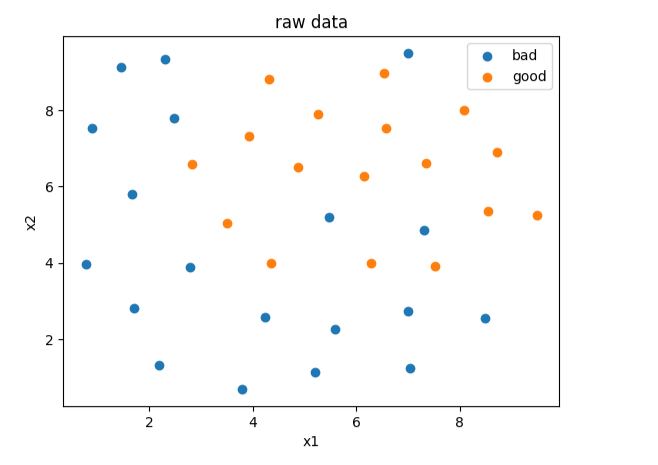
bad = plt.scatter(x1[y==0],x2[y==0])
good = plt.scatter(x1[y==1],x2[y==1])
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend([bad,good],['bad','good'])
plt.show()
#異常檢測,剔除異常點
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.02)
ad_model.fit(x[y==0])
y_predict_bad = ad_model.predict(x[y==0])
print(y_predict_bad)
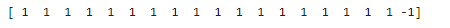
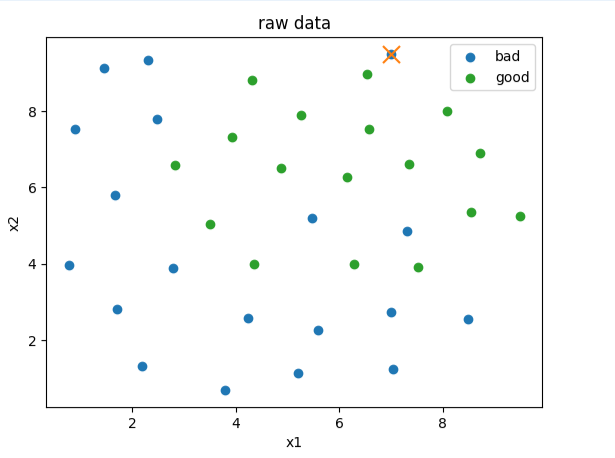
fig2 = plt.figure()
bad = plt.scatter(x1[y==0],x2[y==0])
plt.scatter(x1[y==0][y_predict_bad==-1],x2[y==0][y_predict_bad==-1],marker='x',s=150)
good = plt.scatter(x1[y==1],x2[y==1])
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend([bad,good],['bad','good'])
plt.show()
#處理剔除異常點后的數據,使用數據集data_class_processed.csv,進行主成分分析(PCA)import pandas as pd
import numpy as np
data = pd.read_csv('data_class_processed.csv')#賦值x,y
x = data.drop(['y'],axis=1)
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']
y = data.loc[:,'y']
#PCA預處理
from sklearn.preprocessing import StandardScaler#標準化處理
from sklearn.decomposition import PCA#降維
x_norm = StandardScaler().fit_transform(x)
pca = PCA(n_components=2)
x_reduced = pca.fit_transform(x_norm)
#計算各維度標準差比例
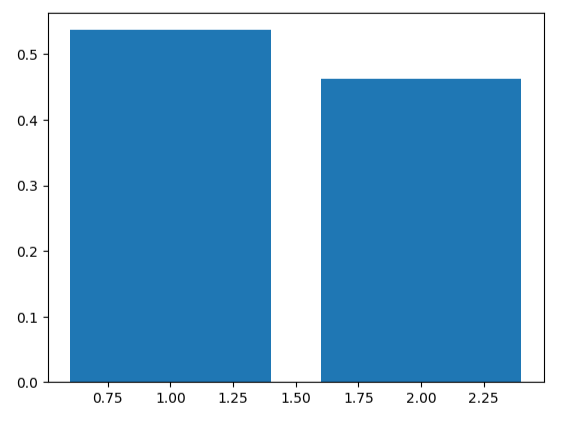
var_ratio = pca.explained_variance_ratio_
print(var_ratio)


#可視化標準差比例
fig3 = plt.figure()
plt.bar([1,2],var_ratio)
plt.show()
#數據分離,分離出訓練數據集和測試數據集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=4,test_size=0.4)
print(x_train.shape,x_test.shape,x.shape)
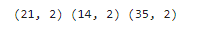
#訓練數據集建立KNN模型,完成分類
from sklearn.neighbors import KNeighborsClassifier
knn_10 = KNeighborsClassifier(n_neighbors=10)
knn_10.fit(x_train,y_train)y_train_predict = knn_10.predict(x_train)
y_test_predict = knn_10.predict(x_test)#計算準確率
from sklearn.metrics import accuracy_score
accuracy_trian = accuracy_score(y_train,y_train_predict)
accuracy_test = accuracy_score(y_test,y_test_predict)
print(accuracy_trian,accuracy_test)
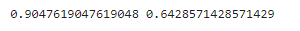
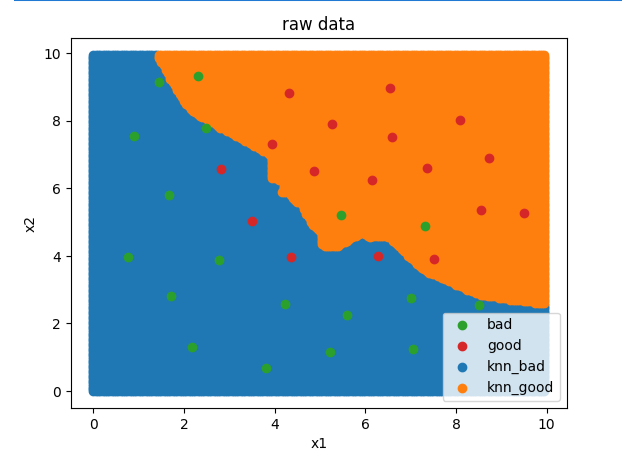
#可視化分類邊界
xx,yy = np.meshgrid(np.arange(0,10,0.05),np.arange(0,10,0.05))
print(xx,yy)

x_range=np.c_[xx.ravel(),yy.ravel()]
print(x_range.shape,x_range)

y_range_predict= knn_10.predict(x_range)
fig4 = plt.figure()
knn_bad = plt.scatter(x_range[:,0][y_range_predict==0],x_range[:,1][y_range_predict==0])
knn_good = plt.scatter(x_range[:,0][y_range_predict==1],x_range[:,1][y_range_predict==1])bad = plt.scatter(x1[y==0],x2[y==0])
good = plt.scatter(x1[y==1],x2[y==1])
plt.title('predict result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend([bad,good,knn_bad,knn_good],['bad','good','knn_bad','knn_good'])
plt.show()
#計算混淆矩陣,計算準確率
from sklearn.metrics import confusion_matrix
cn = confusion_matrix(y_test,y_test_predict)
print(cn)

TP = cn[1,1]
TN = cn[0,0]
FP = cn[0,1]
FN = cn[1,0]
print(TP,TN,FP,FN)

#準確率:整體樣本中,預測正確樣本數的比例
accuracy = (TP + TN)/(TP + TN+ FP+FN)
print(accuracy)
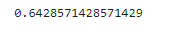
#靈敏度(召回率):正樣本中,預測正確的比例
recall = TP/(TP+FN)
print(recall)#特異度:負樣本中,預測正確的比例
specificity=TN/(TN+FP)
print(specificity)#精確率:預測結果為鄭的樣本中,預測正確的比例
precision = TP/(TP+FP)
print(precision)#F1分數,綜合精確率和召回率的一個判斷標準
f1 = 2*precision*recall/(precision+recall)
print(f1)
#嘗試不同的n_neighbors
n = [i for i in range(1,21)]
accuracy_train = []
accuracy_test = []
for i in n:knn = KNeighborsClassifier(n_neighbors=i)knn.fit(x_train,y_train)y_train_predict = knn.predict(x_train)y_test_predict = knn.predict(x_test)accuracy_train_i = accuracy_score(y_train,y_train_predict)accuracy_test_i = accuracy_score(y_test,y_test_predict)accuracy_train.append(accuracy_train_i)accuracy_test.append(accuracy_test_i)
print(n)
print(accuracy_train)
print(accuracy_test)
fig5 = plt.figure()
plt.subplot(121)
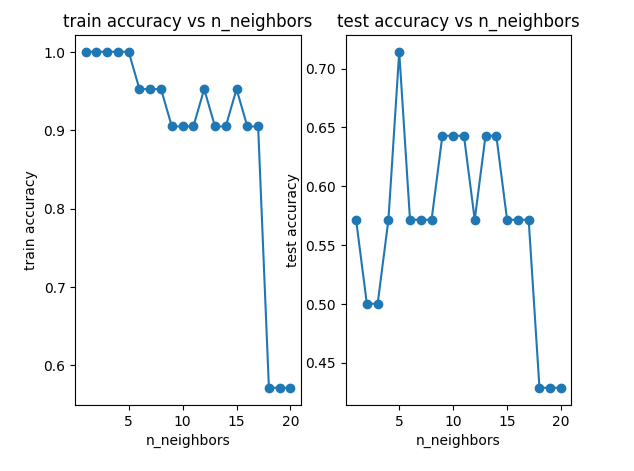
plt.plot(n,accuracy_train,marker='o')
plt.title('train accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.ylabel('train accuracy')plt.subplot(122)
plt.plot(n,accuracy_test,marker='o')
plt.title('test accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.ylabel('test accuracy')
plt.show()






——事件監聽(用戶交互))



)



)




