一、決策樹(Decision Tree)
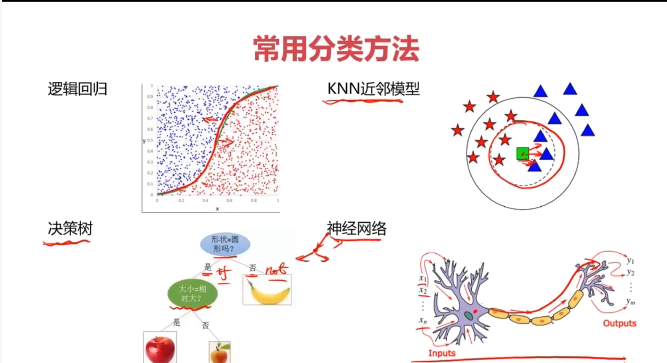
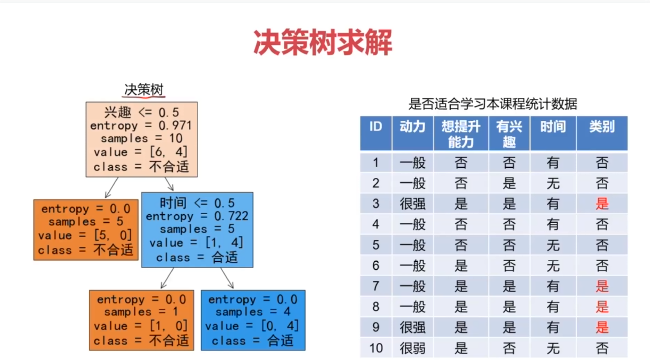
決策樹:一種對實例進行分類的樹形結構,通過多層判斷區分目標所屬類別
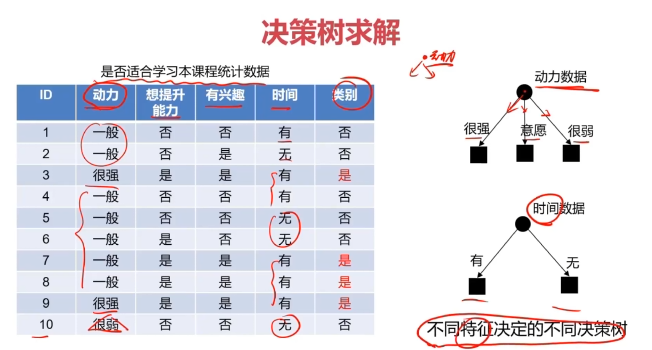
本質:通過多層判斷,從訓練數據集中歸納出一組分類規則
優點:
- 計算量小,運算速度快
- 易于理解,可清晰查看各屬性的重要性
缺點:
- 忽略屬性間的相關性
- 樣本類別分布不均勻時,容易影響模型表現


參考資料:https://www.cnblogs.com/callyblog/p/9724823.html

二、異常檢測(Anomaly Detection)
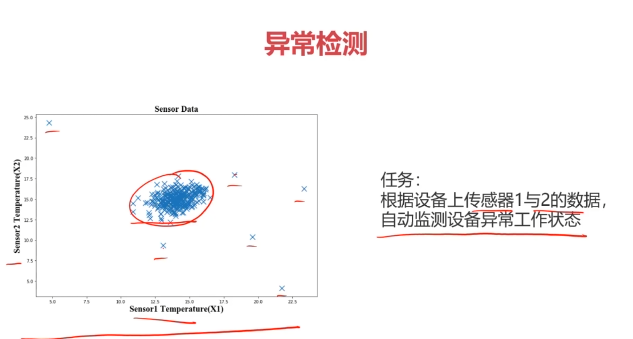
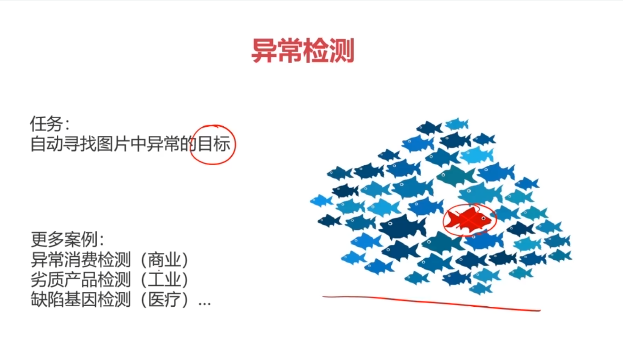
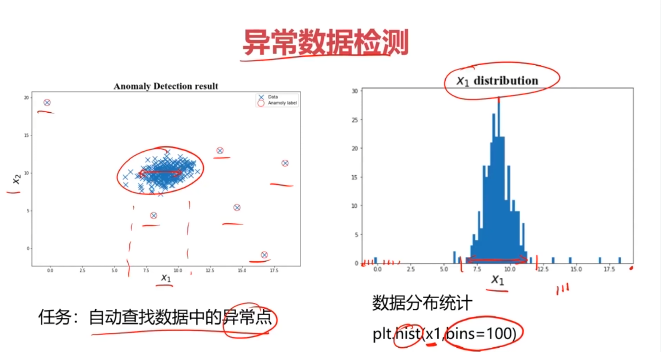
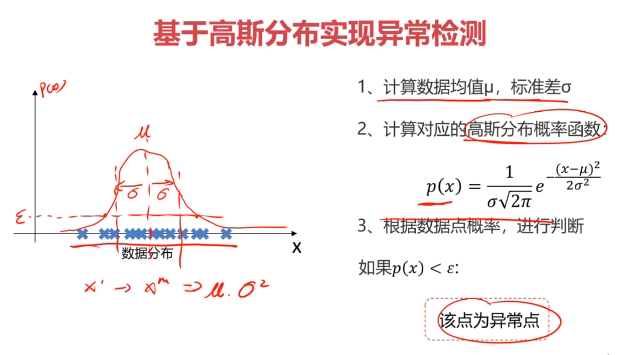
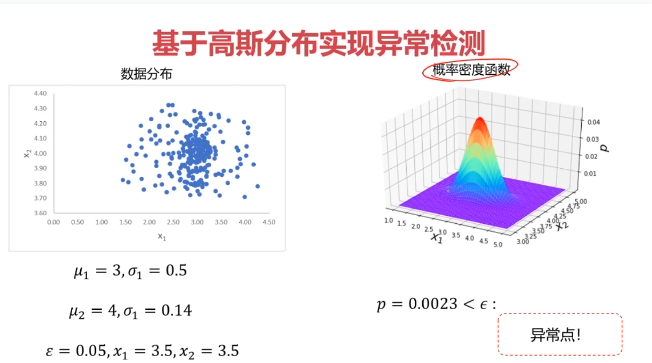
異常檢測:根據輸入數據,對不符合預期模式的數據進行識別
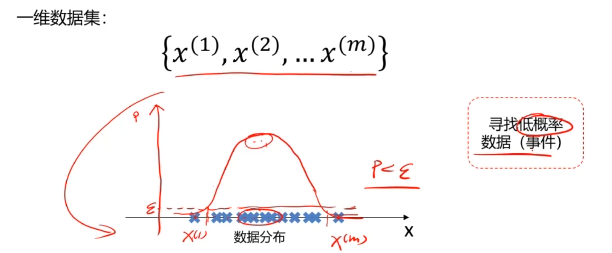
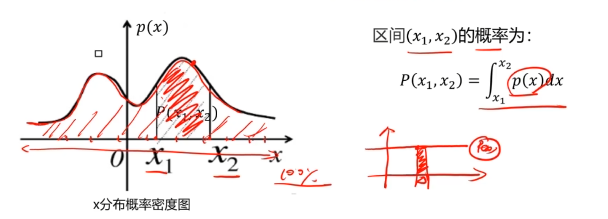
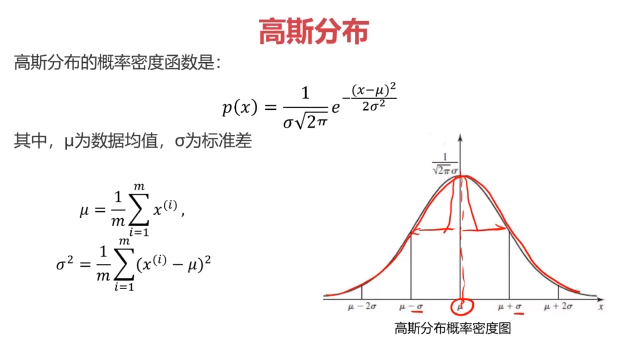
概率密度:概率密度函數是一個描述隨機變量在某個確定取值點附近的可能性的函數
三、主成分分析(PCA)
數據降維(Dimensionality Reduction)
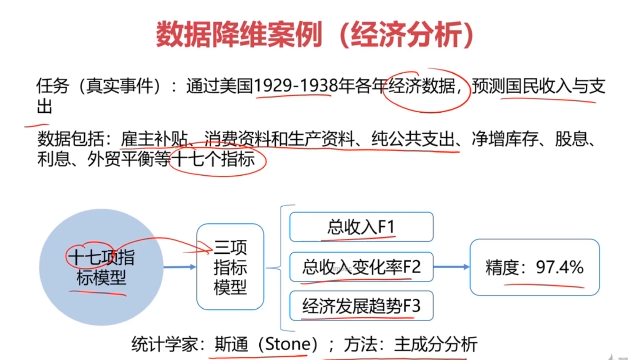
數據降維,是指在某些限定條件下,降低隨機變量個數,得到一組“不相關”主變量的過程。
作用:
- 減少模型分析數據量,提升處理效率,降低計算難度;
- 實現數據可視化。
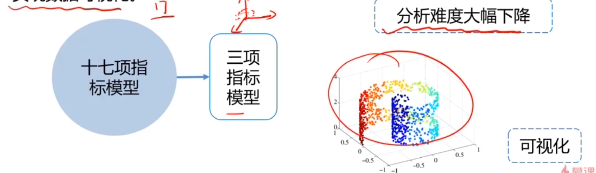
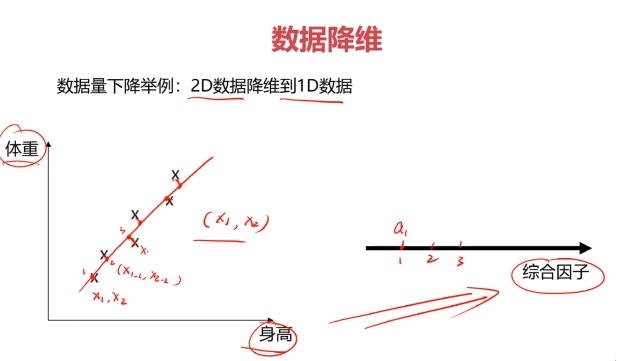
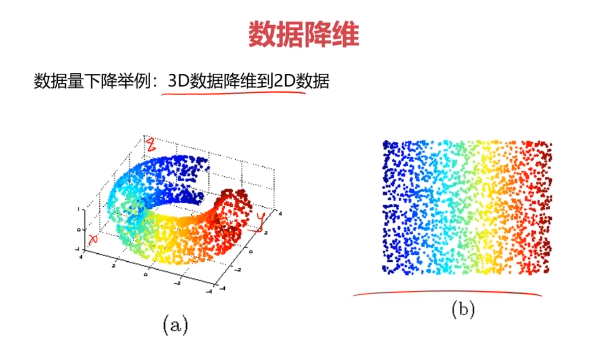
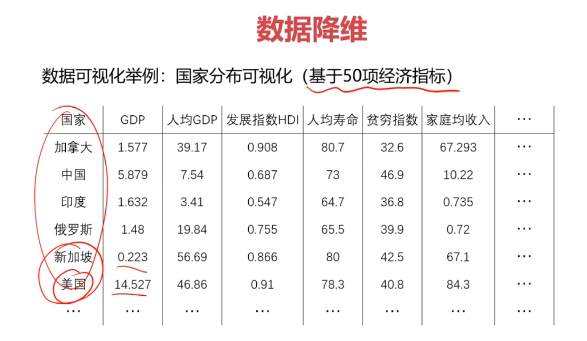
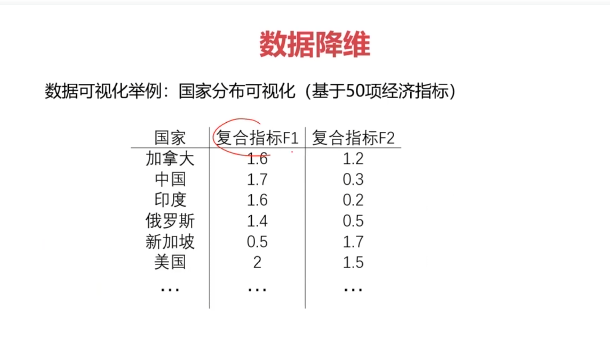
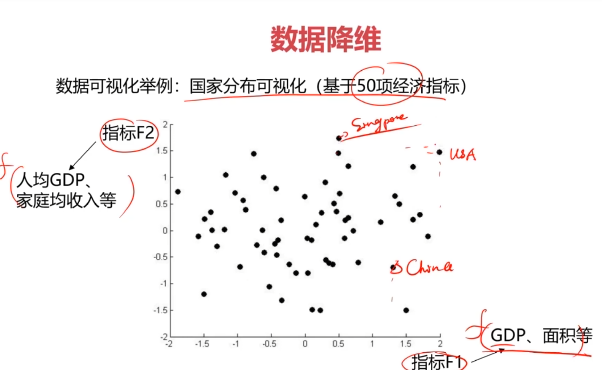
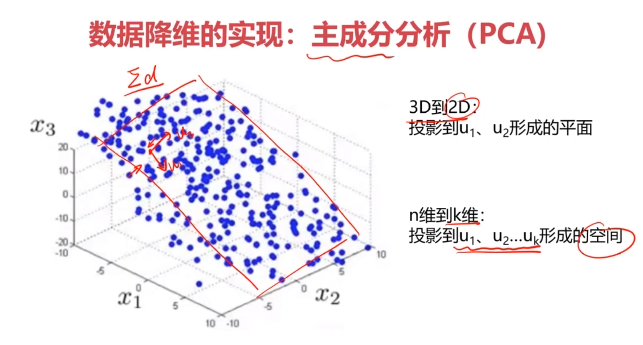
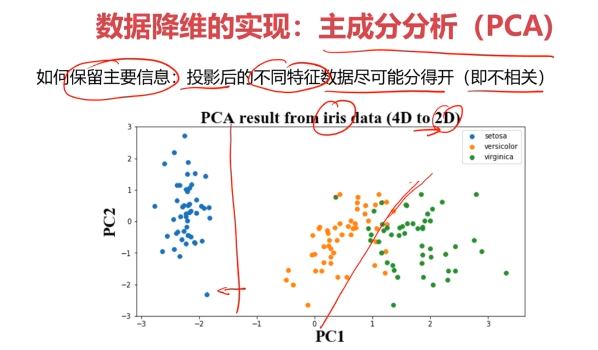
數據降維的實現:主成分分析(PCA)
PCA(principal components analysis):數據降維技術中,應用最最多的方法
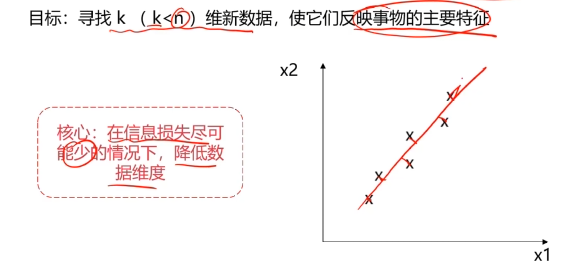

四、Python實戰準備

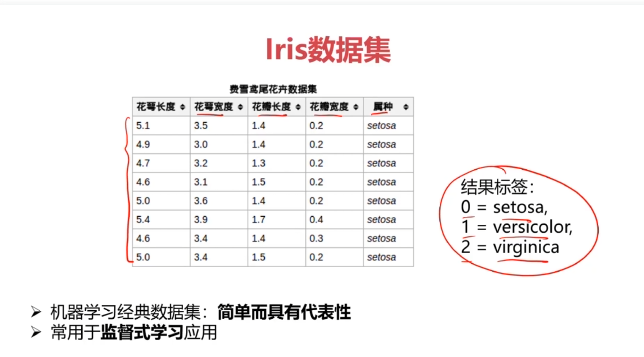
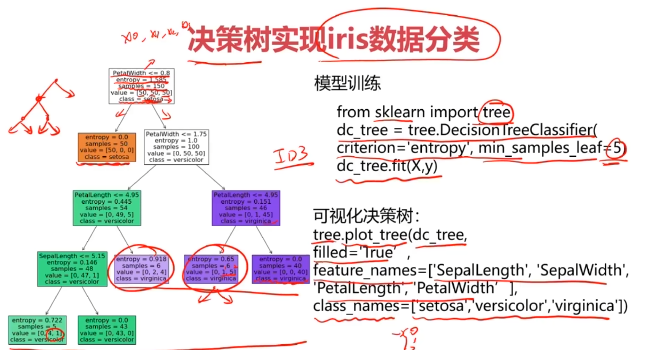
五、實戰:決策樹實現iris數據分類
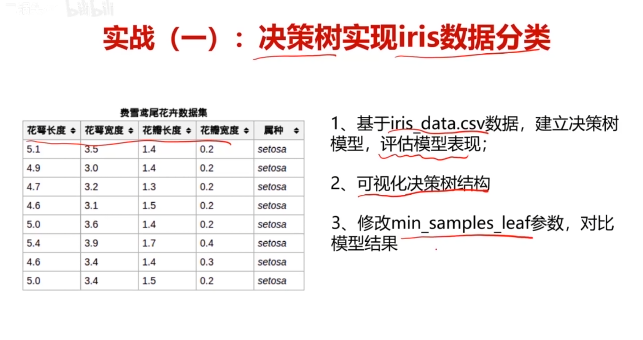
五、決策樹實戰,使用數據集iris_data.csv
#加載數據
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head()
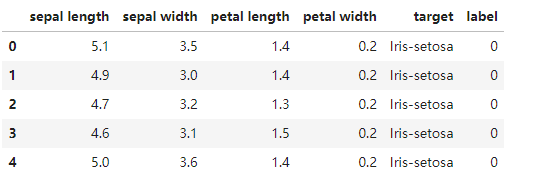
#賦值x,y
x = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(x.shape,y.shape)

#創建決策樹模型
from sklearn import tree
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=5)
dc_tree.fit(x,y)
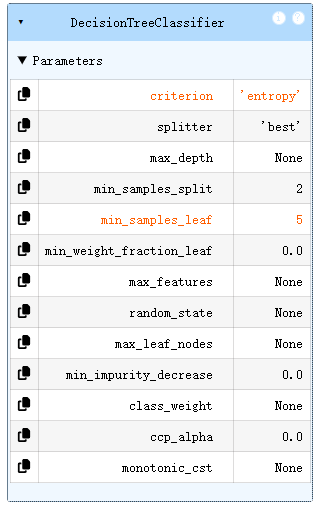
#評估模型表現
y_predict = dc_tree.predict(x)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)
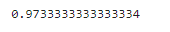
#可視化模型結構
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
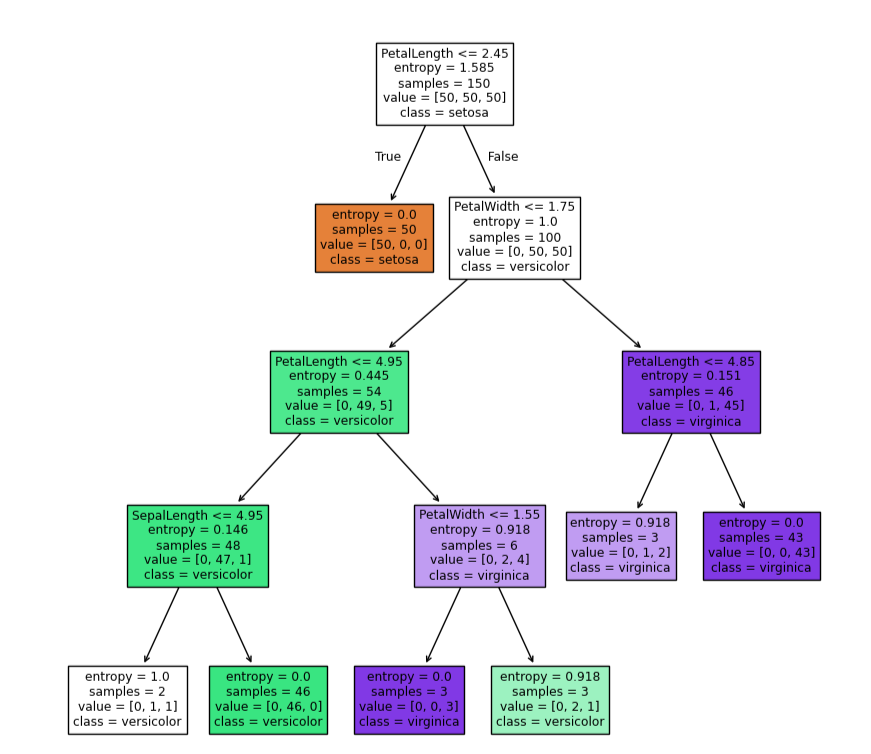
tree.plot_tree(dc_tree,filled=True,feature_names=['SepalLength','SepalWidth','PetalLength','PetalWidth'],class_names=['setosa','versicolor','virginica'])
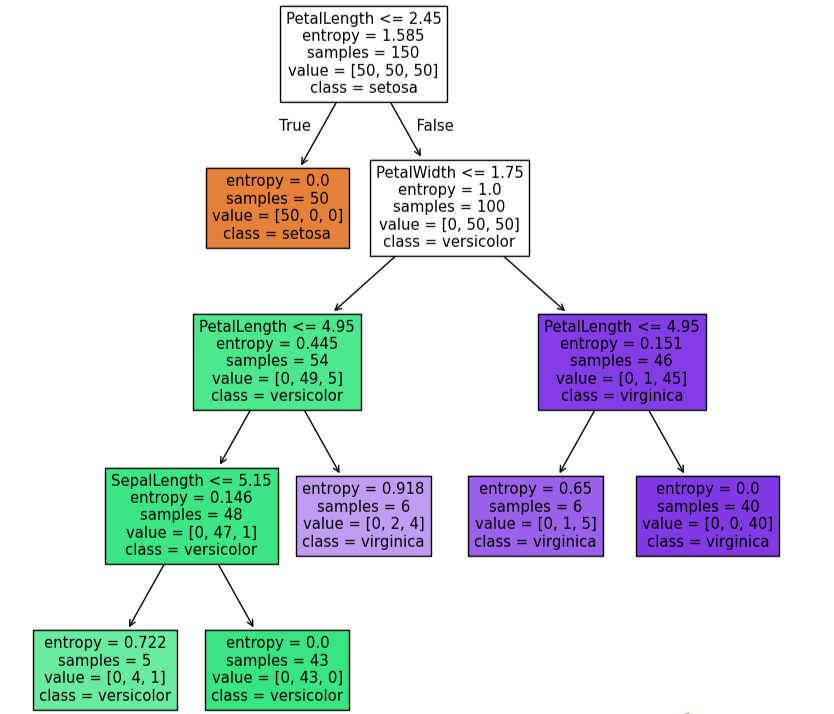
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=2)
dc_tree.fit(x,y)
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree,filled=True,feature_names=['SepalLength','SepalWidth','PetalLength','PetalWidth'],class_names=['setosa','versicolor','virginica'])
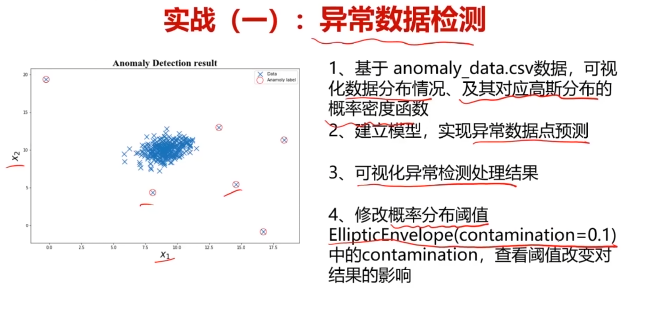
六、異常檢測實戰,使用數據集anomaly_data.csv
#異常檢測
import pandas as pd
import numpy as np
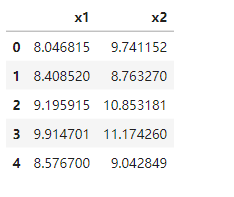
data = pd.read_csv('anomaly_data.csv')
data.head()
from matplotlib import pyplot as plt
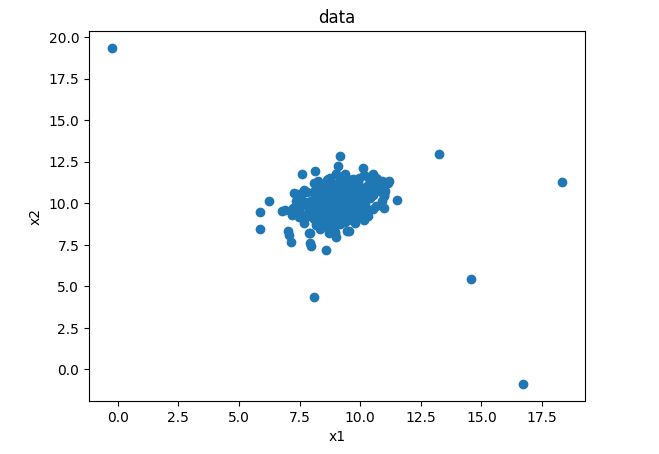
fig3 = plt.figure()
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'])
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
#賦值x,y
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']
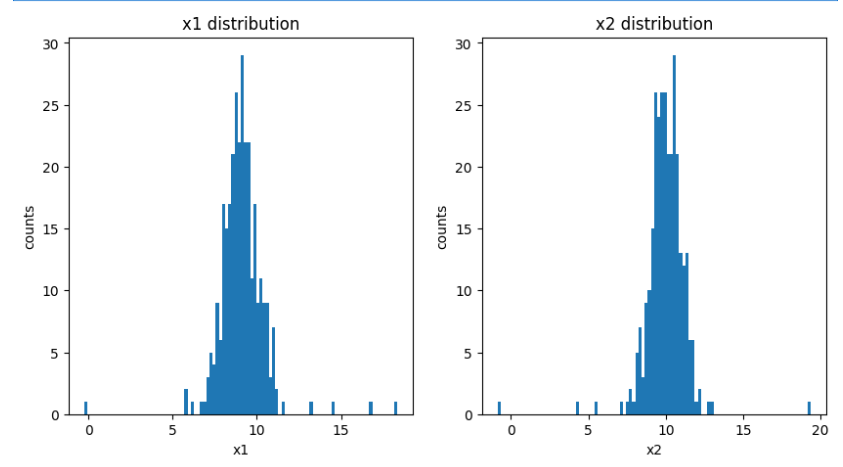
fig4 = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.hist(x1,bins=100)
plt.title('x1 distribution')
plt.xlabel('x1')
plt.ylabel('counts')plt.subplot(122)
plt.hist(x2,bins=100)
plt.title('x2 distribution')
plt.xlabel('x2')
plt.ylabel('counts')
plt.show()
#計算均值和標準差
x1_mean = x1.mean()#均值
x1_signa = x1.std()#標準差
x2_mean = x2.mean()#均值
x2_signa = x2.std()#標準差
print(x1_mean,x1_signa,x2_mean,x2_signa)

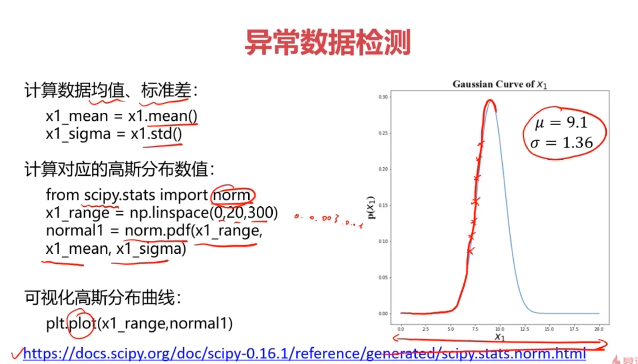
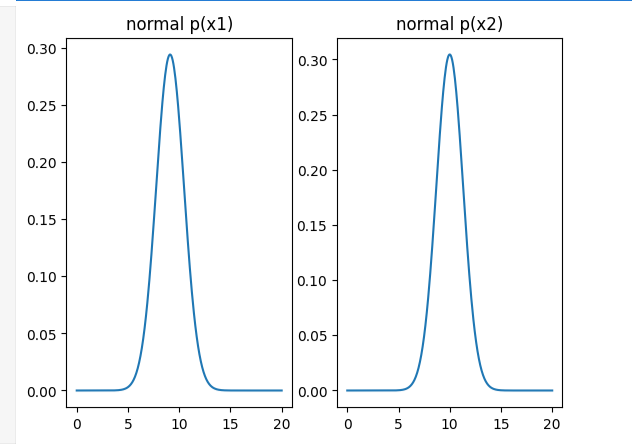
#計算高斯分布密度函數
from scipy.stats import norm
x1_range = np.linspace(0,20,300)
x1_normal = norm.pdf(x1_range,x1_mean,x1_signa)x2_range = np.linspace(0,20,300)
x2_normal = norm.pdf(x2_range,x2_mean,x2_signa)
fig5 = plt.figure()
plt.subplot(121)
plt.plot(x1_range,x1_normal)
plt.title('normal p(x1)')plt.subplot(122)
plt.plot(x2_range,x2_normal)
plt.title('normal p(x2)')
plt.show()
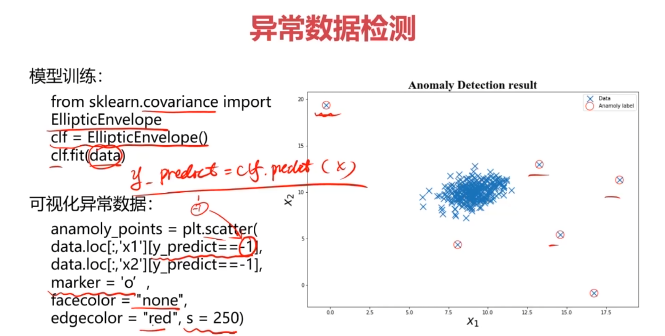
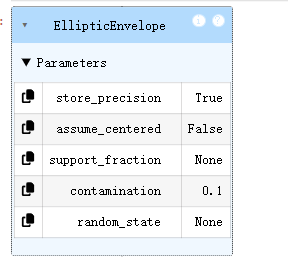
#建立模型
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope()
ad_model.fit(data)
#預測數據
y_predict = ad_model.predict(data)
print(y_predict)

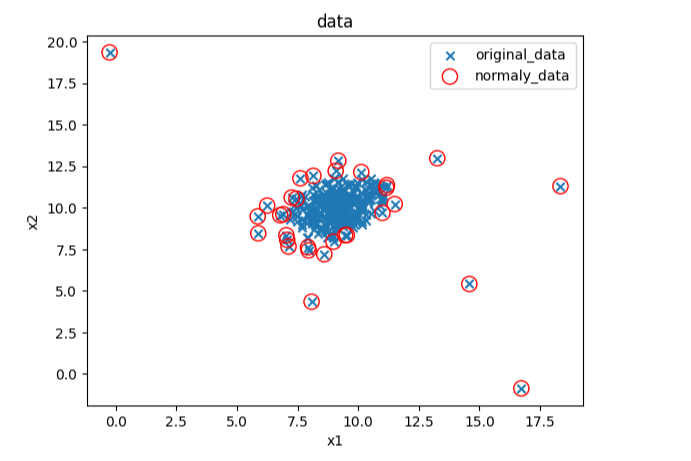
#可視化數據
fig4 = plt.figure()
original_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x')
normaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],marker='o',facecolor='none',edgecolor='red',s=120)
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,normaly_data),('original_data','normaly_data'))
plt.show()
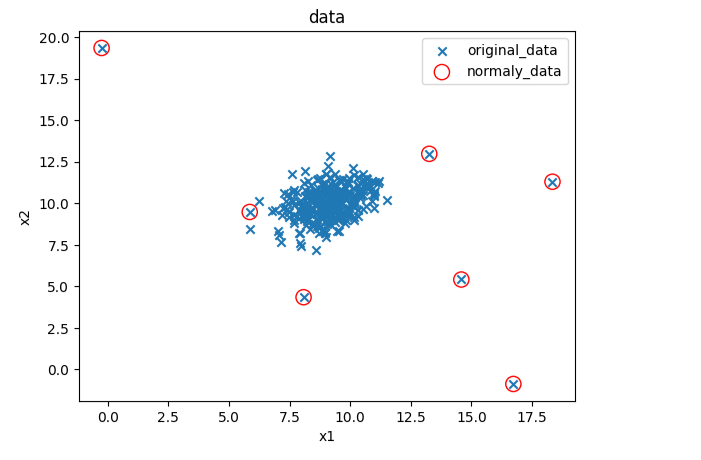
#修改域值大小
ad_model = EllipticEnvelope(contamination=0.02)#默認0.1
ad_model.fit(data)
y_predict = ad_model.predict(data)#可視化數據
fig5 = plt.figure()
original_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x')
normaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],marker='o',facecolor='none',edgecolor='red',s=120)
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,normaly_data),('original_data','normaly_data'))
plt.show()
七、主成分分析(PCA)實戰,使用數據集iris_data.csv
#加載數據
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head()
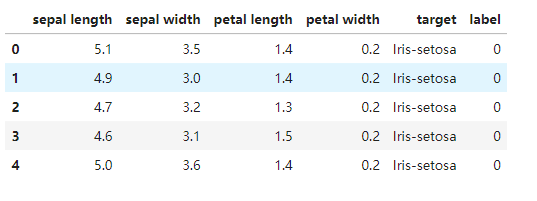
#賦值x,y
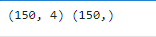
x = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(x.shape,y.shape)
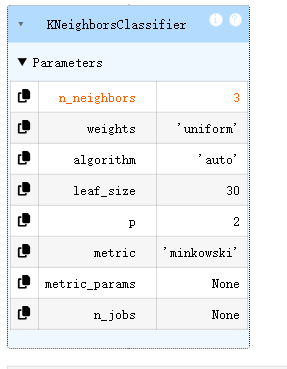
#KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(x,y)
y_predict = KNN.predict(x)from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

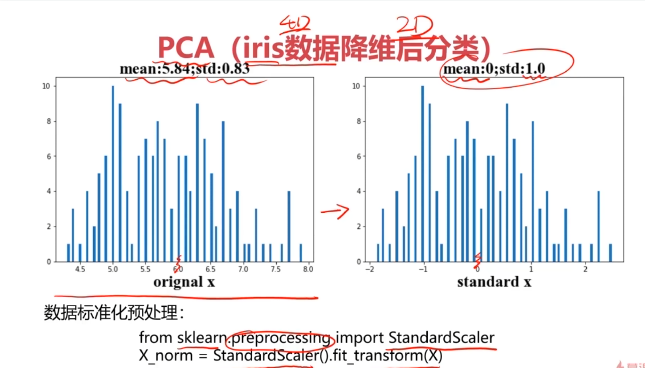
#數據預處理
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(x)
print(X_norm)
#計算均值和標準差
x1_mean = x.loc[:,'sepal length'].mean()
x1_signa = x.loc[:,'sepal length'].std()X_norm_mean = X_norm[:,0].mean()
X_norm_signa = X_norm[:,0].std()print(x1_mean,x1_signa,X_norm_mean,X_norm_signa)

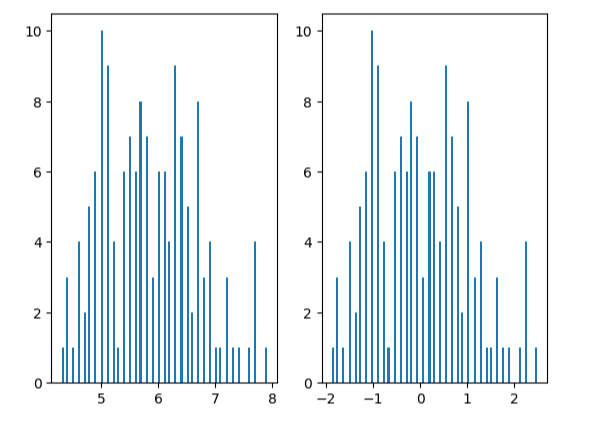
from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.subplot(121)
plt.hist(x.loc[:,'sepal length'],bins=100)plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()
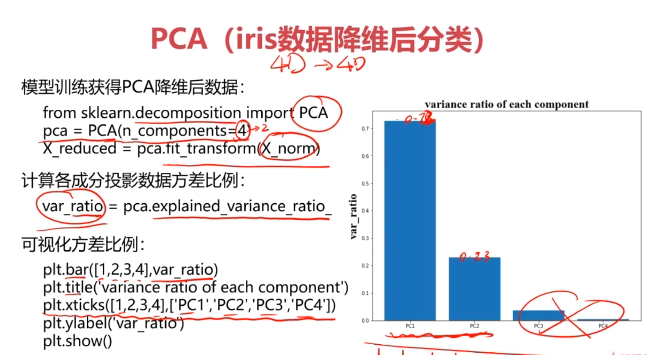
#主成分分析(PCA)
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
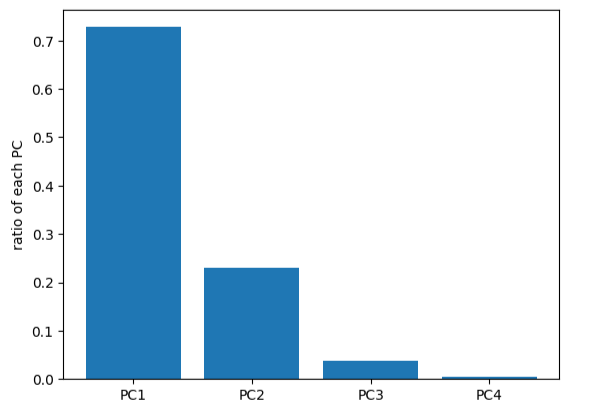
X_pca = pca.fit_transform(X_norm)#計算各個維度方差
var_ratio = pca.explained_variance_ratio_
print(var_ratio)

fig2 = plt.figure()
plt.bar([1,2,3,4],var_ratio)
plt.xticks([1,2,3,4],['PC1','PC2','PC3','PC4'])
plt.ylabel('ratio of each PC')
plt.show()
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_norm)
print(X_pca.shape,type(X_pca))

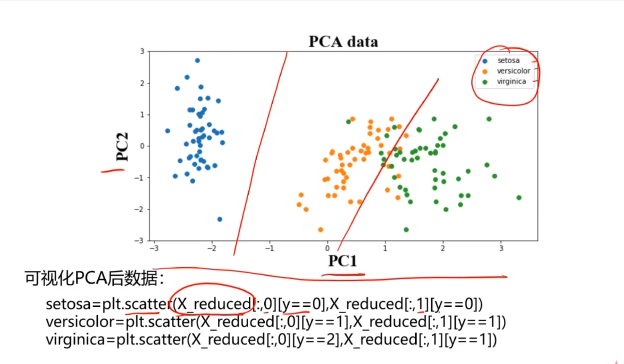
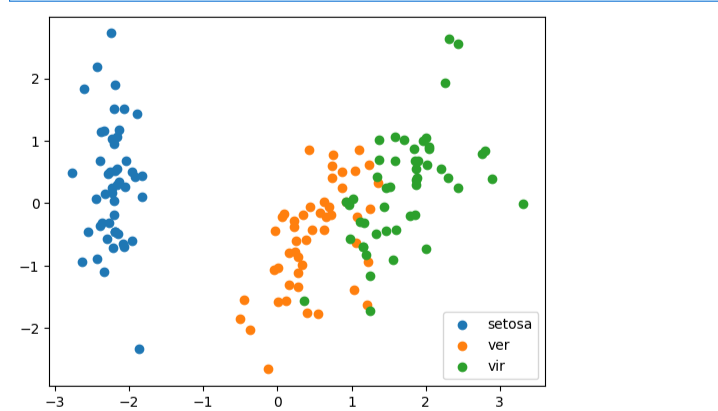
#可視化展示數據
fig3 = plt.figure()
setosa=plt.scatter(X_pca[:,0][y==0],X_pca[:,1][y==0])
ver=plt.scatter(X_pca[:,0][y==1],X_pca[:,1][y==1])
vir=plt.scatter(X_pca[:,0][y==2],X_pca[:,1][y==2])
plt.legend([setosa,ver,vir],['setosa','ver','vir'])
plt.show()
#創建降維后的KNN模型
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)y_predict = KNN.predict(X_pca)from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)
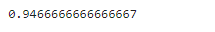







)


,IT營業同步招募)









4:自由進動和弛豫 (Free Precession and Relaxation))
