力扣498 對角線遍歷

問題分析

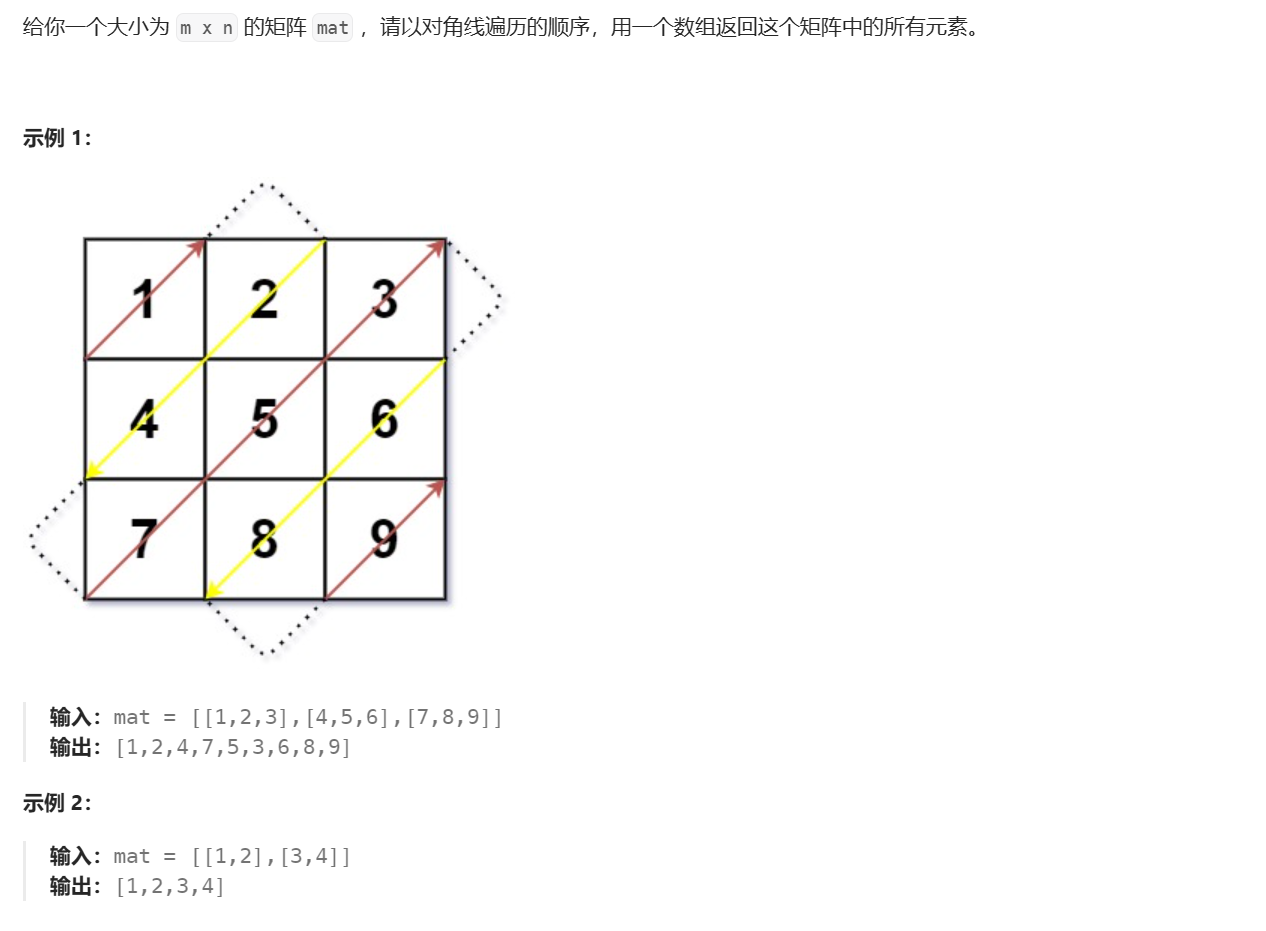
給定一個 m x n 矩陣，我們需要按照對角線順序遍歷所有元素。對角線遍歷的特點是：

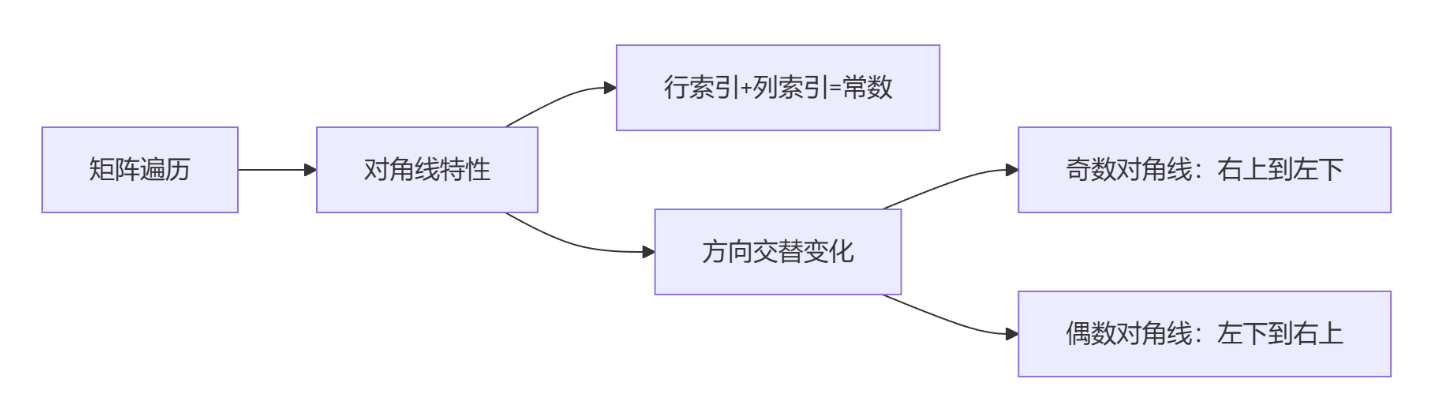
• 每條對角線上元素的行索引與列索引之和為常數
• 遍歷方向交替變化：奇數對角線（從右上到左下），偶數對角線（從左下到右上）

解決方案

核心思路

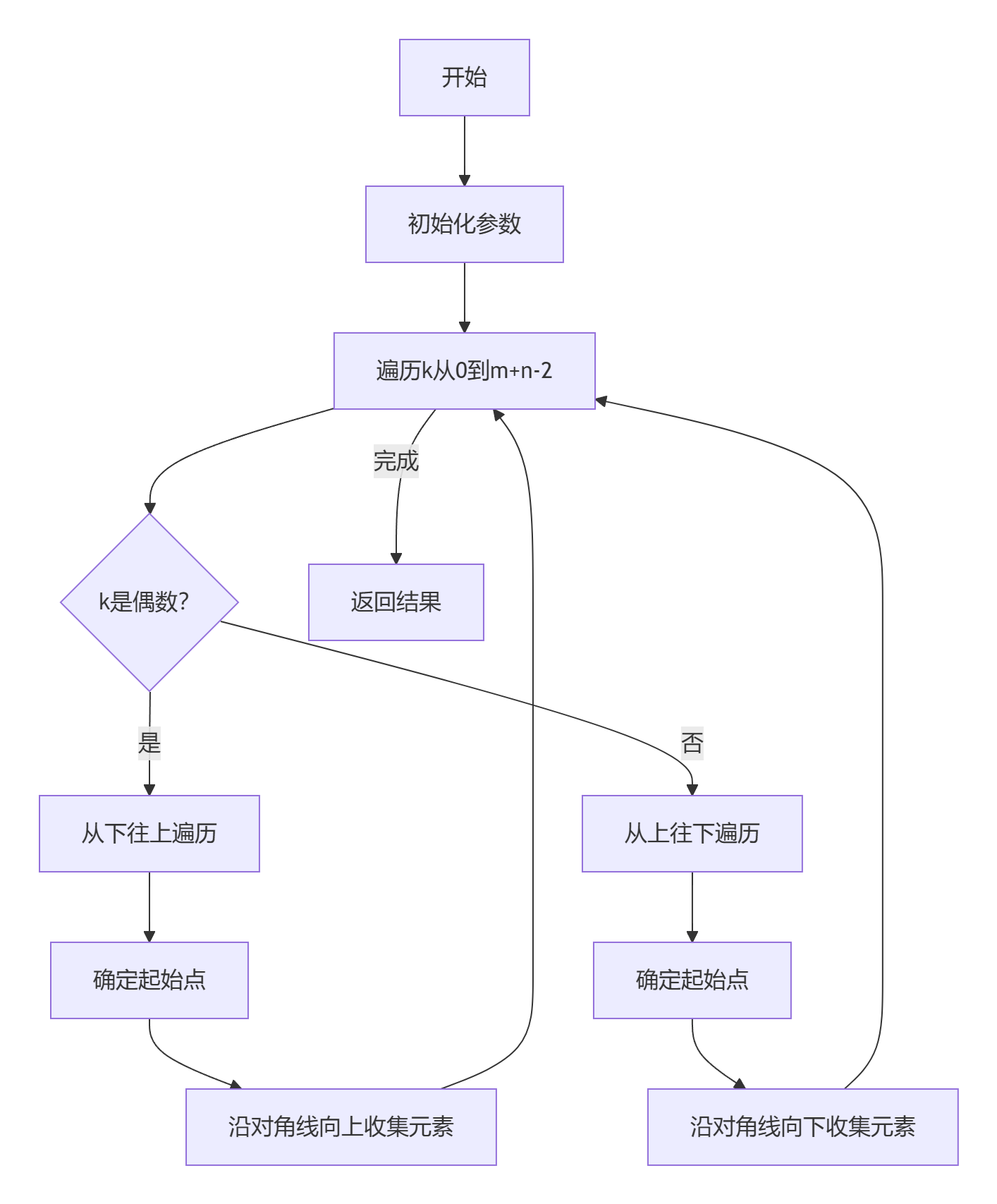
1. 確定對角線常數k：從0到(m-1)+(n-1)
2. 根據k的奇偶性確定遍歷方向：
   • k為偶數：從下往上遍歷（行索引遞減，列索引遞增）
   • k為奇數：從上往下遍歷（行索引遞增，列索引遞減）
3. 確定每條對角線的起始點：
   • 當k < min(m, n)時，起始點在矩陣邊緣
   • 當k ≥ min(m, n)時，起始點向矩陣內部移動

代碼實現

class Solution {public int[] findDiagonalOrder(int[][] mat) {if (mat == null || mat.length == 0) return new int[0];int m = mat.length;int n = mat[0].length;int[] result = new int[m * n];int index = 0;// 遍歷所有對角線（k = i + j）for (int k = 0; k < m + n - 1; k++) {if (k % 2 == 0) { // 偶數對角線：從下往上// 確定起始點int i = Math.min(k, m - 1);int j = k - i;// 沿對角線向上遍歷while (i >= 0 && j < n) {result[index++] = mat[i][j];i--;j++;}} else { // 奇數對角線：從上往下// 確定起始點int j = Math.min(k, n - 1);int i = k - j;// 沿對角線向下遍歷while (j >= 0 && i < m) {result[index++] = mat[i][j];i++;j--;}}}return result;}
}

算法解析

關鍵步驟詳解

邊界處理技巧

1. 起始點確定：
   • 偶數對角線：i = min(k, m-1), j = k - i
   • 奇數對角線：j = min(k, n-1), i = k - j
2. 遍歷終止條件：
   • 當行索引或列索引超出矩陣邊界時停止
3. 方向切換：
   • 利用k的奇偶性自然切換方向

復雜度分析

指標	值	說明
時間復雜度	O(m*n)	每個元素訪問一次
空間復雜度	O(1)	除結果數組外無額外空間
遍歷效率	100%	最優解

拓展思考

變體問題

1. Z字形打印矩陣
2. 螺旋矩陣遍歷
3. 對角線求和問題

總結

對角線遍歷問題展示了如何通過觀察矩陣的數學特性（行索引+列索引=常數）來設計高效算法。關鍵在于：

1. 識別對角線遍歷的數學規律
2. 巧妙處理遍歷方向的交替變化
3. 精確控制邊界條件