????????本節我們分享使用RANSAC算法進行點云的擬合。RANSAC算法是什么?不知道的同學們前排罰站!(前面有)
????????總的來說,RANSAC(Random Sample Consensus)是一種通用的迭代魯棒估計框架,無論擬合何種幾何模型,其思想完全一致: ?1. 隨機采樣 → 2. 最小樣本擬合 → 3. 內點判定 → 4. 模型評估 → 5. 迭代收斂 → 6. 輸出最優模型。 ?
下面按“直線、平面、一般二次曲面、二維圓、三維球面、圓柱面”六種情形,給出統一的實現步驟與關鍵公式,便于對照查閱。
--------------------------------
1. 擬合 3D 空間直線
--------------------------------
隨機采樣 ?
- 每次隨機抽取 2 個點 p?、p?(兩點確定一條直線)。模型估計 ?
- 方向向量 v = (p? ? p?) / ‖p? ? p?‖ ?
- 直線方程:L(t) = p? + t v,t∈?內點判定 ?
- 點 p 到直線的距離 ?
d = ‖(p ? p?) × v‖ ?
若 d < d_th,則為內點。迭代終止 ?
- 最大迭代次數 N 或內點比例達到要求即可停止。--------------------------------
2. 擬合 3D 平面
--------------------------------
隨機采樣 ?
- 每次隨機抽取 3 個不共線的點 p?,p?,p?。模型估計 ?
- 平面法向量 n = (p? ? p?) × (p? ? p?) 并歸一化 ?
- 平面方程:n·(x ? p?)=0,即 ax+by+cz+d=0內點判定 ?
- 點 p 到平面距離 ?
d = |a·x + b·y + c·z + d| / √(a2+b2+c2) ?
若 d < d_th,則為內點。--------------------------------
3. 擬合一般二次曲面
--------------------------------
隨機采樣 ?
- 二次曲面一般式 Ax2+By2+Cz2+Dxy+Eyz+Fzx+Gx+Hy+Iz+J=0 共 10 個參數,因此最少需要 9 個點(秩缺 1,需額外約束 J=1 或 ‖參數‖=1)。模型估計 ?
- 構造設計矩陣 A ∈ ?^{m×9} 和觀測向量 b ∈ ?^m,用最小二乘解參數向量 θ=[A,B,…,I]^T。 ?
- 得到隱式曲面方程 f(x,y,z)=0。內點判定 ?
- 點 p 到隱式曲面的代數距離 |f(p)| / ‖?f(p)‖ 與閾值比較。--------------------------------
4. 擬合 2D 圓
--------------------------------
隨機采樣 ?
- 每次隨機抽取 3 個非共線的 2D 點 (x?,y?),(x?,y?),(x?,y?)。模型估計 ?
- 圓心 (a,b) 和半徑 r 的閉合公式 ?
a = [ (x?2+y?2?x?2?y?1)(y??y?) ? (x?2+y?2?x?2?y?2)(y??y?) ] / D ?
b = [ (x?2+y?2?x?2?y?2)(x??x?) ? (x?2+y?2?x?2?y?2)(x??x?) ] / D ?
D = 2[(x??x?)(y??y?) ? (x??x?)(y??y?)] ?
r = √[(x??a)2+(y??b)2]內點判定 ?
- 點 (x,y) 到圓的距離 ?
|√[(x?a)2+(y?b)2] ? r| < d_th。--------------------------------
5. 擬合 3D 球面
--------------------------------
隨機采樣 ?
- 每次隨機抽取 4 個非共面 3D 點 p?…p?。模型估計 ?
- 球心 c 和半徑 R 的線性方程組 ?
‖p_i ? c‖2 = R2, i=1…4 → 4 線性方程 → 解 c、R。內點判定 ?
- 點 p 到球面距離 ?
|‖p ? c‖ ? R| < d_th。--------------------------------
6. 擬合 3D 圓柱面
--------------------------------
隨機采樣 ?
- 每次隨機抽取 5 個 3D 點(圓柱面有 7 個自由度,但 5 點可解唯一參數,見下)。模型估計 ?
- 將圓柱面參數化為: ?
中心軸:直線 L(t)=c + t d(方向向量 d,單位化) ?
半徑 r ?
- 5 點約束:任意點 p_i 到軸的距離等于 r ?
‖(p_i ? c) × d‖ = r, i=1…5 ?
可通過非線性最小二乘或幾何代數法一次性求出 d、c、r。內點判定 ?
- 點 p 到圓柱面距離 ?
|‖(p ? c) × d‖ ? r| < d_th。
--------------------------------
下面書寫一段RANSAC的統一處理流程(偽代碼)
--------------------------------
輸入:點云 Q,幾何模型類型 T,閾值 d_th,最大迭代 N ?
for k = 1…N ?
S ← RandomSample(Q, m) ? ? ? ? ? # m 由模型決定(2,3,4,5…) ?
M ← FitModel(S, T) ? ? ? ? ? ? ? # 見上各小節 ?
Inliers ← {p ∈ Q | Distance(p,M) < d_th} ?
if |Inliers| > best_inliers ?
best_model ← M ?
best_inliers ← Inliers ?
輸出:best_model, best_inliers
可視化 ?
- 用 Open3D / Matplotlib / PCL 等庫將原始點云和擬合幾何體(直線、平面、網格化曲面、圓環、球體、圓柱網格)同時渲染。
????????至此,六種常見幾何模型的 RANSAC 實現步驟全部給出,可直接對照代碼模板進行落地。當然,本次的數據豬腳依然是我們的老朋友——兔砸!
一、RANSAC各種擬合程序
import open3d as o3d
import numpy as np
import pyransac3d as pyrsc
import randomFILE = "E:/CSDN/規則點云/bunny.pcd" # 改成自己的文件# ---------------- 通用工具 -----------------
def load_pcd():pcd = o3d.io.read_point_cloud(FILE)if not pcd.has_points():raise RuntimeError("找不到 {}".format(FILE))return pcd, np.asarray(pcd.points)def show(title, in_pcd, out_pcd, geom):"""統一可視化"""o3d.visualization.draw_geometries([in_pcd, out_pcd, geom],window_name=title,width=800, height=600)# AXIS = o3d.geometry.TriangleMesh.create_coordinate_frame(size=1)# ---------------- 1. 直線 -----------------
def fit_line(pcd, pts):def ransac_3d(points, thresh=0.05, max_iter=1000):best_in, best_model = [], Nonefor _ in range(max_iter):idx = random.sample(range(len(points)), 2)p1, p2 = points[idx]vec = p2 - p1if np.linalg.norm(vec) < 1e-6:continuevec = vec / np.linalg.norm(vec)dists = np.linalg.norm(np.cross(points - p1, vec), axis=1)inliers = np.where(dists < thresh)[0]if len(inliers) > len(best_in):best_in = inliersbest_model = (p1, vec)return best_model, best_inmodel, idx = ransac_3d(pts, 0.05, 1000)if model is None:print("直線擬合失敗")returnp1, vec = modelin_pcd = pcd.select_by_index(idx).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(idx, invert=True).paint_uniform_color([0,1,0])length = np.linalg.norm(pcd.get_max_bound() - pcd.get_min_bound())start, end = p1 - vec * length, p1 + vec * lengthls = o3d.geometry.LineSet(points=o3d.utility.Vector3dVector([start, end]),lines=o3d.utility.Vector2iVector([[0,1]]))ls.colors = o3d.utility.Vector3dVector([[0,0,1]])show("1. 直線擬合", in_pcd, out_pcd, ls)# ---------------- 2. 平面 -----------------
def fit_plane(pcd, pts):plane = pyrsc.Plane()eq, idx = plane.fit(pts, thresh=0.01, maxIteration=1000)in_pcd = pcd.select_by_index(idx).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(idx, invert=True).paint_uniform_color([0,1,0])# 平面網格aabb = in_pcd.get_axis_aligned_bounding_box()size = max(aabb.get_extent()) * 1.5mesh = o3d.geometry.TriangleMesh.create_box(size, size, 0.001)mesh.translate([-size/2, -size/2, 0])mesh.rotate(in_pcd.get_rotation_matrix_from_xyz((0,0,0)), center=(0,0,0))normal = np.array(eq[:3])z = np.array([0,0,1])if np.linalg.norm(np.cross(z, normal)) > 1e-6:rot = o3d.geometry.get_rotation_matrix_from_axis_angle(np.cross(z, normal))mesh.rotate(rot, center=(0,0,0))mesh.translate(in_pcd.get_center())mesh.paint_uniform_color([0,0,1])mesh.compute_vertex_normals()show("2. 平面擬合", in_pcd, out_pcd, mesh)# ---------------- 3. 二次曲面 -----------------
def fit_quadric(pcd, pts):"""擬合二次曲面 z = a x2 + b y2 + c xy + d x + e y + f用 RANSAC 選 6 個內點,然后用最小二乘解 6 參數。"""def quadric_model(pts_sample):A = np.c_[pts_sample[:,0]**2, pts_sample[:,1]**2,pts_sample[:,0]*pts_sample[:,1],pts_sample[:,0], pts_sample[:,1],np.ones(len(pts_sample))]b = pts_sample[:,2]coeffs, *_ = np.linalg.lstsq(A, b, rcond=None)return coeffsdef residuals(pts, coeffs):a,b,c,d,e,f = coeffsreturn np.abs(pts[:,2] - (a*pts[:,0]**2 + b*pts[:,1]**2 + c*pts[:,0]*pts[:,1] + d*pts[:,0] + e*pts[:,1] + f))best_in, best_coeff = [], Nonefor _ in range(1000):idx = random.sample(range(len(pts)), 6)sample = pts[idx]try:coeff = quadric_model(sample)except np.linalg.LinAlgError:continuedists = residuals(pts, coeff)inliers = np.where(dists < 0.05)[0]if len(inliers) > len(best_in):best_in, best_coeff = inliers, coeffif best_coeff is None:print("二次曲面擬合失敗")returnin_pcd = pcd.select_by_index(best_in).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(best_in, invert=True).paint_uniform_color([0,1,0])# 網格可視化aabb = in_pcd.get_axis_aligned_bounding_box()xx, yy = np.meshgrid(np.linspace(aabb.min_bound[0], aabb.max_bound[0], 50),np.linspace(aabb.min_bound[1], aabb.max_bound[1], 50))a,b,c,d,e,f = best_coeffzz = a*xx**2 + b*yy**2 + c*xx*yy + d*xx + e*yy + fvertices = np.stack([xx.ravel(), yy.ravel(), zz.ravel()], axis=1)mesh = o3d.geometry.TriangleMesh()mesh.vertices = o3d.utility.Vector3dVector(vertices)idx = np.arange(50*50).reshape(50,50)triangles = []for i in range(49):for j in range(49):triangles.append([idx[i,j], idx[i+1,j], idx[i,j+1]])triangles.append([idx[i+1,j], idx[i+1,j+1], idx[i,j+1]])mesh.triangles = o3d.utility.Vector3iVector(np.array(triangles))mesh.paint_uniform_color([0,0,1])mesh.compute_vertex_normals()show("3. 曲面擬合", in_pcd, out_pcd, mesh)# ---------------- 4. 圓 -----------------
def fit_circle(pcd, pts):pts2d = pts[:, :2] # 假設圓在 XY 平面def ransac_circle(pts2d, thresh=0.05, max_iter=1000):best_in, best_model = [], Nonefor _ in range(max_iter):idx = random.sample(range(len(pts2d)), 3)A,B,C = pts2d[idx]D = 2*((B[0]-A[0])*(C[1]-A[1]) - (B[1]-A[1])*(C[0]-A[0]))if abs(D) < 1e-6: continuecx = ((C[1]-A[1])*(B[0]**2+B[1]**2-A[0]**2-A[1]**2) - (B[1]-A[1])*(C[0]**2+C[1]**2-A[0]**2-A[1]**2)) / Dcy = ((B[0]-A[0])*(C[0]**2+C[1]**2-A[0]**2-A[1]**2) - (C[0]-A[0])*(B[0]**2+B[1]**2-A[0]**2-A[1]**2)) / Dr = np.linalg.norm([A[0]-cx, A[1]-cy])dists = np.abs(np.linalg.norm(pts2d - [cx,cy], axis=1) - r)inliers = np.where(dists < thresh)[0]if len(inliers) > len(best_in):best_in, best_model = inliers, (cx, cy, r)return best_model, best_inmodel, idx = ransac_circle(pts2d, 0.05, 1000)if model is None:print("圓擬合失敗")returncx,cy,r = modelin_pcd = pcd.select_by_index(idx).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(idx, invert=True).paint_uniform_color([0,1,0])theta = np.linspace(0, 2*np.pi, 100)x = cx + r*np.cos(theta)y = cy + r*np.sin(theta)z = np.zeros_like(x)circle_pts = np.vstack([x,y,z]).Tls = o3d.geometry.LineSet(points=o3d.utility.Vector3dVector(circle_pts),lines=o3d.utility.Vector2iVector([[i,(i+1)%100] for i in range(100)]))ls.colors = o3d.utility.Vector3dVector([[0,0,1] for _ in range(100)])show("4. 圓擬合", in_pcd, out_pcd, ls)# ---------------- 5. 球 -----------------
def fit_sphere(pcd, pts):sph = pyrsc.Sphere()center, radius, idx = sph.fit(pts, thresh=0.05, maxIteration=1000)in_pcd = pcd.select_by_index(idx).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(idx, invert=True).paint_uniform_color([0,1,0])mesh = o3d.geometry.TriangleMesh.create_sphere(radius=radius)mesh.translate(center)mesh.paint_uniform_color([0,0,1])mesh.compute_vertex_normals()show("5. 球擬合", in_pcd, out_pcd, mesh)# ---------------- 6. 圓柱 -----------------
def fit_cylinder(pcd, pts):cyl = pyrsc.Cylinder()axis, center, radius, idx = cyl.fit(pts, thresh=0.05, maxIteration=1000)in_pcd = pcd.select_by_index(idx).paint_uniform_color([1,0,0])out_pcd = pcd.select_by_index(idx, invert=True).paint_uniform_color([0,1,0])height = np.linalg.norm(pcd.get_max_bound() - pcd.get_min_bound()) * 1.2mesh = o3d.geometry.TriangleMesh.create_cylinder(radius=radius, height=height, resolution=50)mesh.compute_vertex_normals()mesh.paint_uniform_color([0,0,1])z = np.array([0,0,1])axis = axis / np.linalg.norm(axis)if np.linalg.norm(np.cross(z, axis)) > 1e-6:rot = o3d.geometry.get_rotation_matrix_from_axis_angle(np.cross(z, axis))mesh.rotate(rot, center=(0,0,0))mesh.translate(center)show("6. 圓柱擬合", in_pcd, out_pcd, mesh)# ---------------- 主菜單 -----------------
def main():pcd, pts = load_pcd()menu = """
1 直線
2 平面
3 二次曲面
4 圓
5 球
6 圓柱
q 退出
請選擇(1-6):"""while True:choice = input(menu).strip()if choice == 'q': breakif choice not in {'1','2','3','4','5','6'}:print("輸入無效")continueif choice == '1': fit_line(pcd, pts)if choice == '2': fit_plane(pcd, pts)if choice == '3': fit_quadric(pcd, pts)if choice == '4': fit_circle(pcd, pts)if choice == '5': fit_sphere(pcd, pts)if choice == '6': fit_cylinder(pcd, pts)if __name__ == "__main__":main()二、RANSAC各種擬合結果
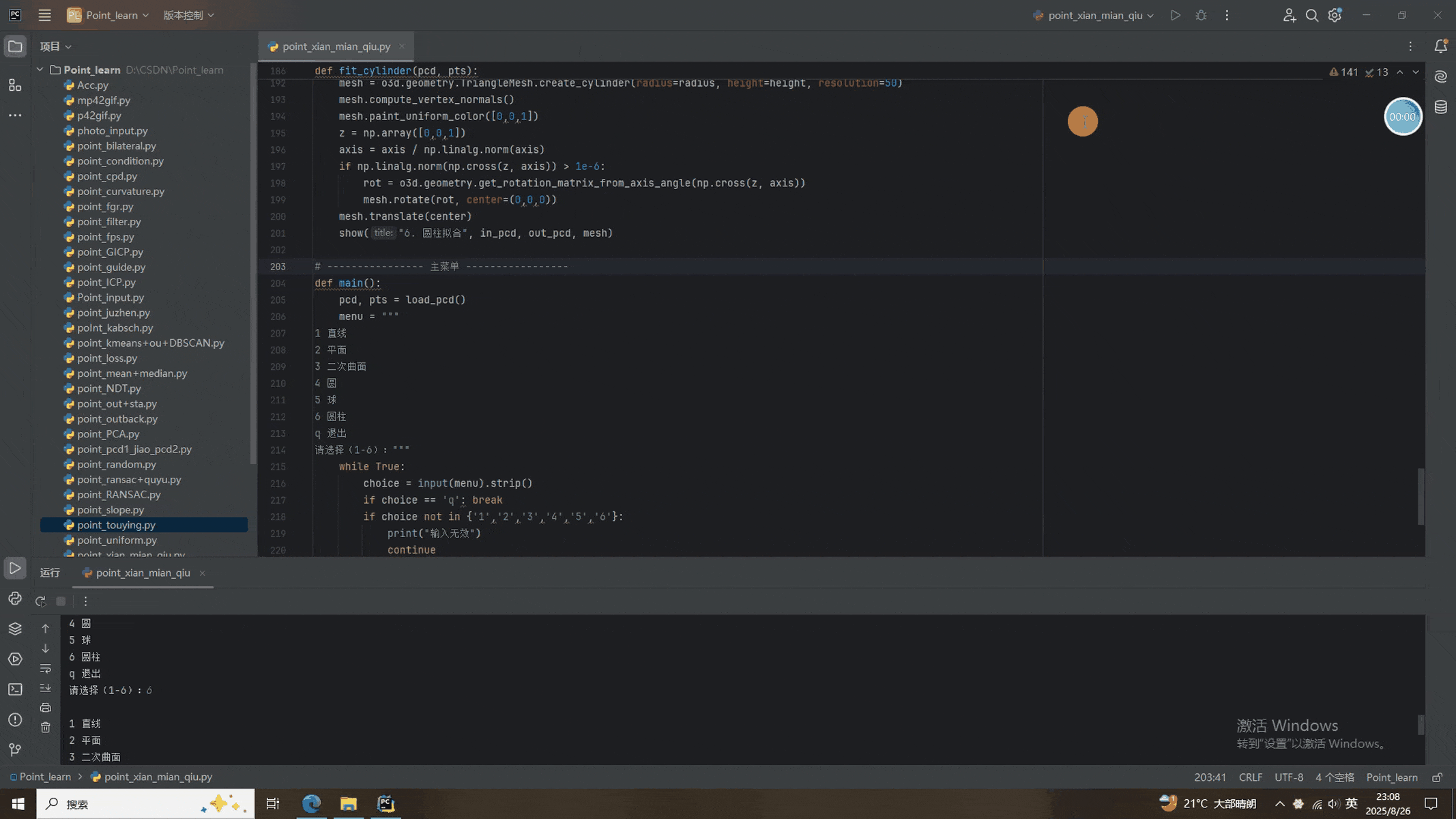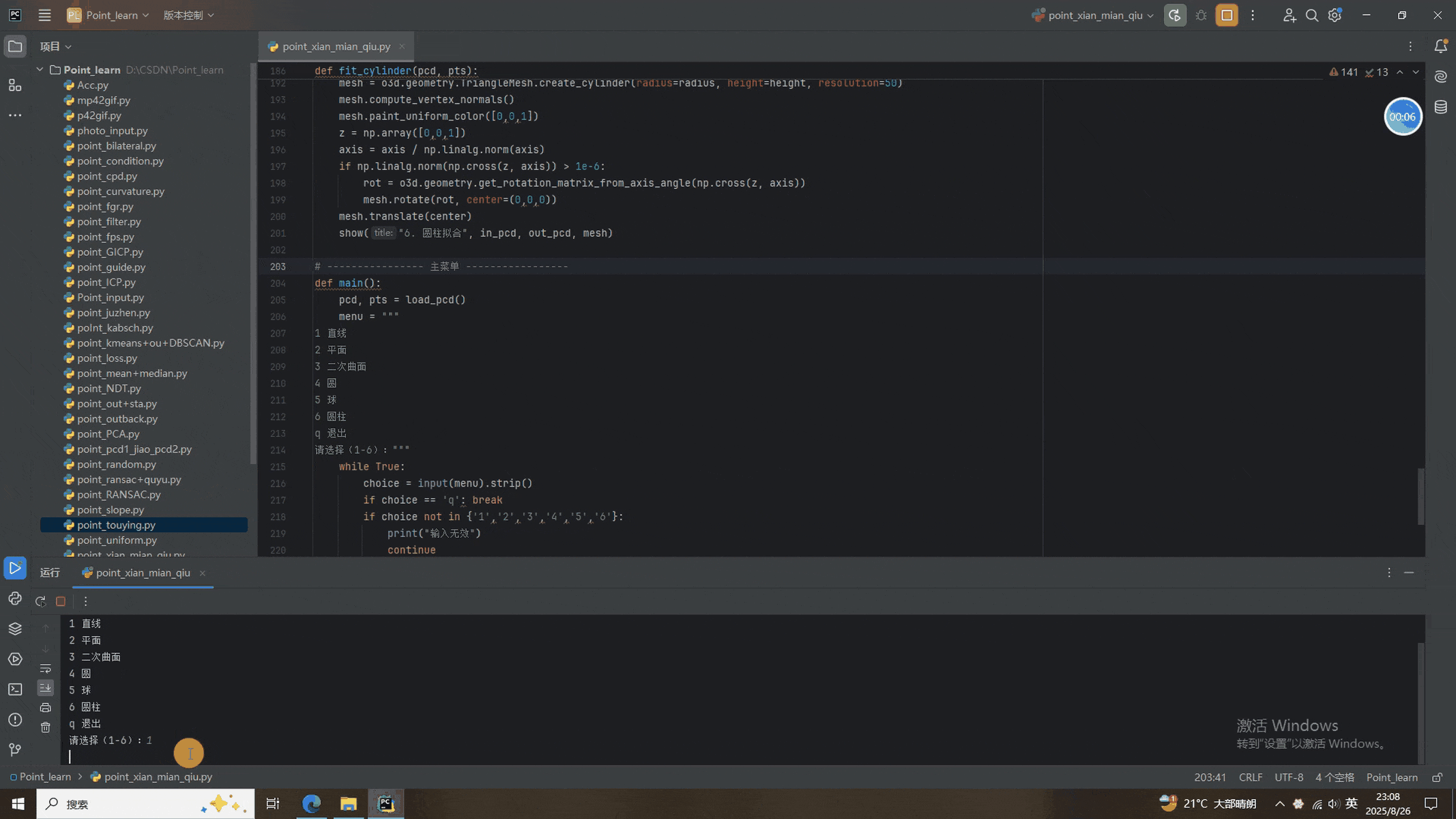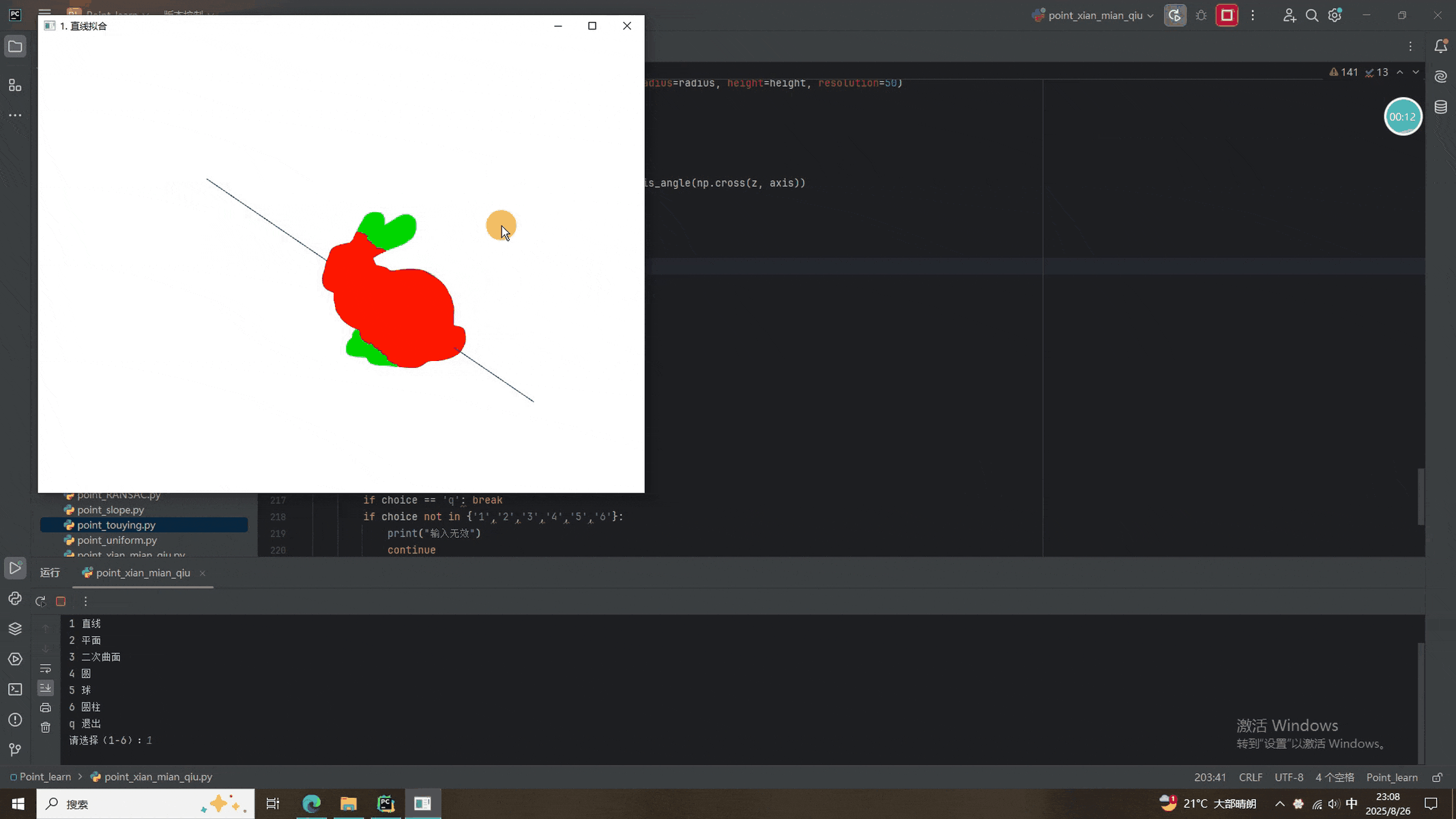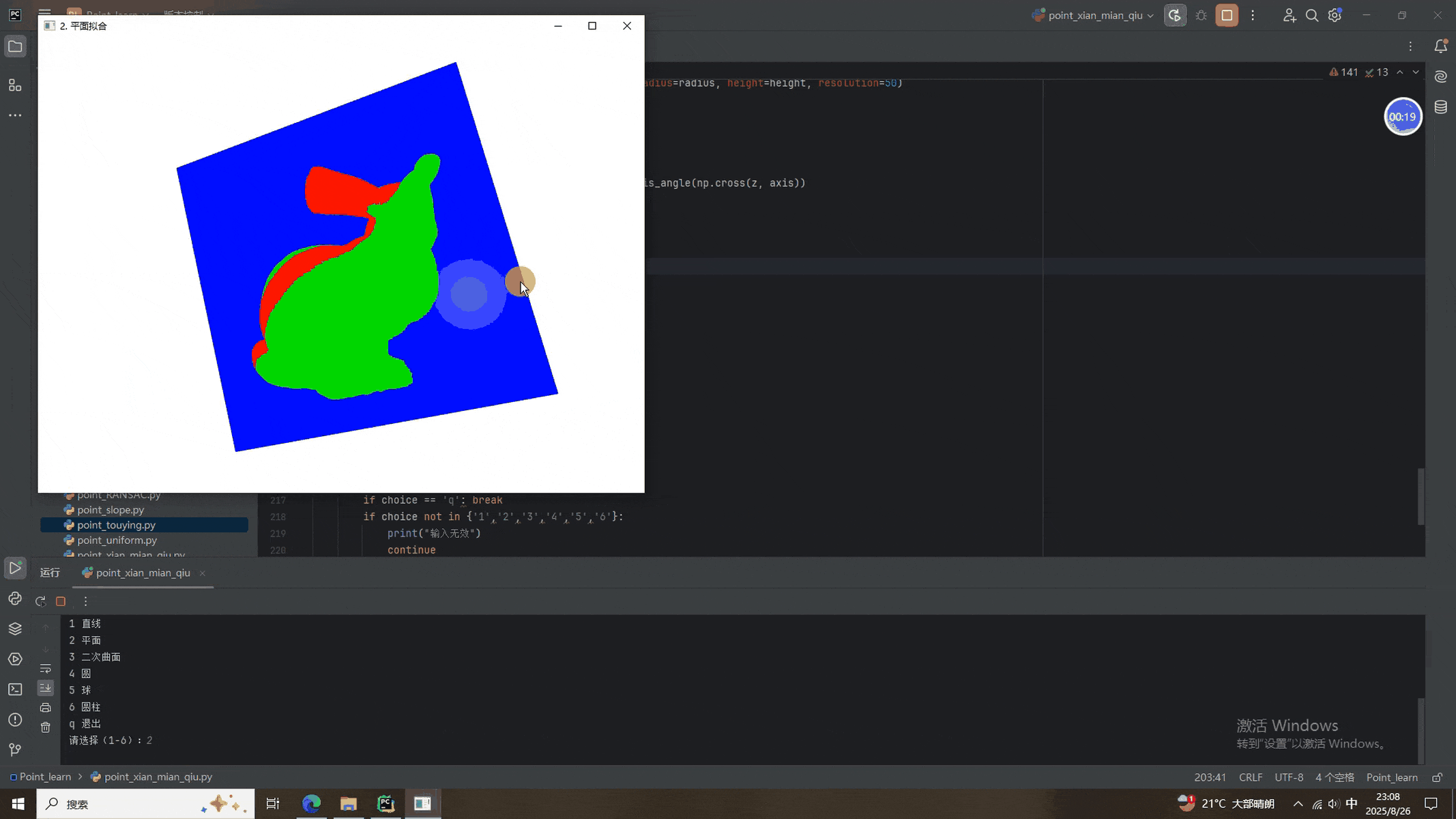
????????本次的程序添加了選擇按鈕,1-6分別是RANSAC擬合直線、平面、曲面、圓、球面、圓柱面。除了圓柱面擬合過于離譜(主要兔砸長得不像柱子),其他的都挺好。
就醬,下次見^-^

 Google Chrome 越界讀寫漏洞【內附EXP】)






)








)

