分治思想
分(Divide):將待排序數組不斷拆分為兩個等長(或近似等長)的子數組,直到子數組長度為 1(天然有序)。
治(Conquer):遞歸排序每個子數組。
合(Merge):將兩個已排序的子數組合并為一個更大的有序數組,重復此過程直到合并為完整的有序數組。
歸并排序
- 基本步驟:
1.遞歸拆分:
計算數組中點 mid,將數組分為左子區間 [left, mid] 和右子區間 [mid+1, right]。
遞歸拆分左右子區間,直到子區間長度為 1(left >= right 時終止遞歸)。
2.合并有序子區間:
用兩個指針分別遍歷左右兩個有序子區間,每次將較小的元素放入臨時數組 tmp。
處理剩余未遍歷完的子區間,將剩余元素追加到 tmp 中。將 tmp 中的有序元素拷貝回原數組的對應位置。
- 關鍵特點
1.時間復雜度:
最好 / 最壞 / 平均情況均為 O(n log n)。原因:拆分過程產生 log n 層遞歸,每層合并總耗時 O(n)。
2.空間復雜度:
O(n),需額外的臨時數組 tmp 存儲合并結果。
3.穩定性:
穩定排序。當元素相等時,左區間元素先放入臨時數組,保持原相對順序。
4.適用場景:
適合大規模數據排序(時間復雜度穩定)。
適合鏈表排序(可通過指針操作實現 O (1) 額外空間,避免數組拷貝開銷)。
不適合內存受限場景(需額外空間)。
一. (75.) 顏色分類

解法:
類?數組分兩塊的算法思想,這?是將數組分成三塊,可以再添加?個指針。此題還可以用內置接口sort(開始迭代器,結束迭代器)來直接做
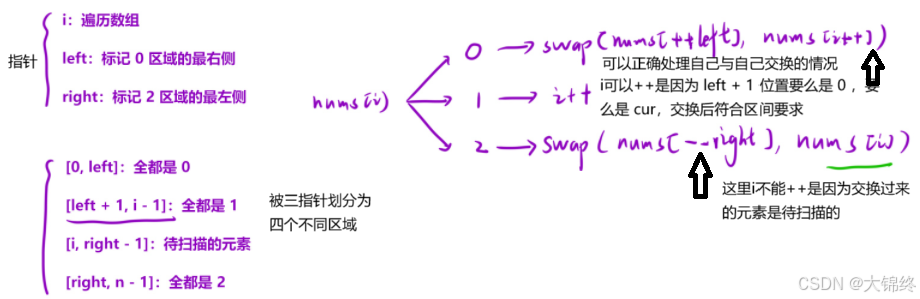
class Solution {
public:void sortColors(vector<int>& nums) {//將left和right置-1和n位置是為了保證區間內首元素交換正確int left=-1,right=nums.size(),cur=0;while(cur<right){if(nums[cur]==0) swap(nums[++left],nums[cur++]);else if(nums[cur]==1) cur++;else if(nums[cur]==2) swap(nums[--right],nums[cur]);}}
};
二. (912.) 排序數組-快排

快速排序(劃分三數組實現優化)
算法原理:
快排最核?的?步就是 Partition (分割數據):將數據按照?個標準,分成左右兩部分。
隨機選擇基準算法流程:
函數設計:int randomKey(vector& nums, int left, int right)
a. 在主函數那?種?顆隨機數種?;
b. 在隨機選擇基準函數這??成?個隨機數;
c. 由于我們要隨機產??個基準,因此可以將隨機數轉換成隨機下標:讓隨機數 % 上區間??,然后加上區間的左邊界即可。
快速排序算法主要流程:
a. 定義遞歸出?;
b. 利?隨機選擇基準函數?成?個基準元素;
c. 將數組劃分為 左 中 右 三部分:左邊是?基準元素?的數據,中間是與基準元素相同的數據,右邊是?基準元素?的數據。
d. 遞歸處理左邊區域和右邊區域。
采取數組分三塊的思想實現快排:
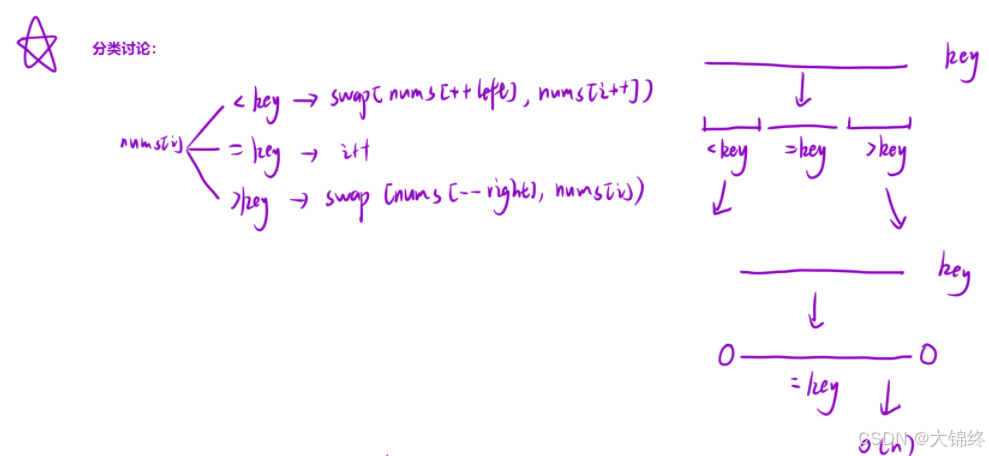
時間復雜度:
時間復雜度為NlogN,,遞歸調用棧的深度為logN,算法導論中概率求期望證明
快速排序每次劃分后,需要遞歸處理左右兩個子區間,總工作量是:
O(n) + O(n/2) + O(n/2) + O(n/4) + O(n/4) + … = O(n log n)(每次遞歸的兩個子區間工作量相加,導致總規模是 n log n)。
class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//種下一顆隨機數種子qsort(nums,0,nums.size()-1);return nums;}void qsort(vector<int>& nums,int left,int right){if(left>=right) return;//遞歸返回條件//獲取隨機數,自定義函數int key = getRandom(nums, left, right);int l=left-1,i=left,r=right+1;while(i<r){//注意條件判斷只能走一次,防止i一直++后>right超出范圍if(nums[i]<key) swap(nums[++l],nums[i++]);else if(nums[i]==key) i++;else if(nums[i]>key) swap(nums[--r],nums[i]);}qsort(nums,left,l);//遞歸處理qsort(nums,r,right);}int getRandom(vector<int>& nums,int left,int right){int r=rand();return nums[r%(right-left+1)+left];}
};
三. (215.) 數組中的第K個最?元素

優先級隊列方法:
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int> st(nums.begin(),nums.end());//for(int i=0;i<k-1;i++)while(--k){st.pop();}return st.top();}
};
快速選擇排序方法:
思路:
依舊是通過獲取隨機數當key,快排將數組分為三塊的方法,但是計算每一個區間的數量與k進行比較,選擇相應區間遞歸一次即可獲得結果
分情況討論:
將數組劃分三塊后,只能保證大小順序,但每個區域內部還是無序狀態,所以還要進行遞歸,本題的優勢在于根據第k大,可以選擇一個區域遞歸。
時間復雜度:
快速選擇只處理一個子區間,避免了另一半的工作量,因此總時間復雜度從 O (n log n) 降至 O (n)。
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));//可以這么記s代表start,即開始隨機數return qsort(nums,k,0,nums.size()-1);}int qsort(vector<int>& nums,int k,int left,int right){//每一個區域都是從左往右遍歷,所以返回nums[左下標]if(left>=right) return nums[left];int key=getrandom(nums,left,right);//將數組分為三塊int i=left,l=left-1,r=right+1;while(i<r){if(nums[i]<key) swap(nums[++l],nums[i++]);else if(nums[i]==key) i++;else swap(nums[--r],nums[i]);}//劃分區間,選擇性遞歸int b=r-l-1,c=right-r+1;//獲取中,右區間元素,左邊通過前兩者可得if(c>=k) return qsort(nums,k,r,right);if(b+c>=k) return key;else return qsort(nums,k-b-c,left,l);}int getrandom(vector<int>nums,int left,int right){int r=rand();return nums[r%(right-left+1)+left];}
};
四. (劍指 Offer 40.) 最小的k個數

思路:
和第三題相同,區別在于從求第k大的元素變成求k個最小的元素,主邏輯相同,利用隨機選擇快排將數組分三塊,我們的目的就是將前k個最小的元素放到數組前k個位置,其他位置順序不用考慮
情況討論:

abc分別為小、等于、大三個區間元素的個數。
五. (912.) 排序數組-歸并

簡單對比歸并與快排
解法:
題目與二相同,但采取歸并解法
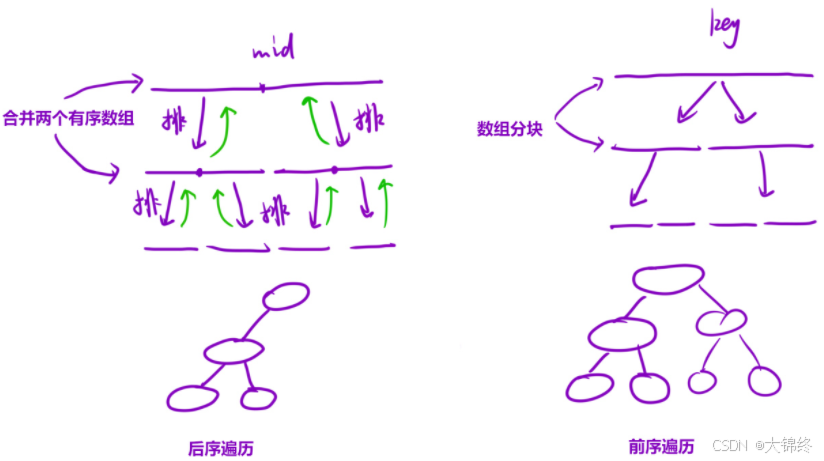
快排與歸并本質思想都相同,分區間處理問題,只是處理問題的時機不同,歸并排序類似于二叉樹的后序遍歷,快排相當于二叉樹的前序遍歷。
1.歸并就是先遞歸到最底層,然后逐層排序左區間和右區間一層層由小及大返回
2.快排是每一層先排序好了再往下由大到小遞歸
class Solution {
public:vector<int> sortArray(vector<int>& nums) {int*tmp=(int *)malloc(sizeof(int)*nums.size());mergesort(nums,0,nums.size()-1,tmp);return nums;}void mergesort(vector<int>& nums,int left,int right,int *tmp){if(left>=right) return;int mid=(right+left)>>1;//與除2操作等價,但位運算效率更高mergesort(nums,left,mid,tmp);//遞歸處理左右子區間mergesort(nums,mid+1,right,tmp);//歸并int begin1=left,begin2=mid+1;int i=left;//臨時變量來遍歷while(begin1<=mid&&begin2<=right){if(nums[begin1]<nums[begin2]) tmp[i++]=nums[begin1++];else tmp[i++]=nums[begin2++];}//排序其中一個區間剩下的元素while(begin1<=mid){tmp[i++]=nums[begin1++];}while(begin2<=right){tmp[i++]=nums[begin2++];}//將排序后元素拷貝回臨時數組for(int i=left;i<=right;i++){nums[i]=tmp[i];}}};
也可以采取這樣的方式定義類成員函數
class Solution
{vector<int> tmp;
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());
效率差異:
1.malloc 僅做 “內存分配”,開銷集中在與操作系統的內存管理交互(如查找空閑內存塊)。
2.resize 不僅分配內存,還涉及 “對象管理”,resize 會在分配內存后對新元素進行初始化,內部還需要維護 size、capacity 等成員變量的更新,所以開銷會比malloc大一些
六. (劍指 Offer 51.) 數組中的逆序對

解法:
- 暴力解法
兩層for循環,依次對每個元素可能的逆序對做查找,會超時
- 歸并排序
運用分治思想,遞歸將數組分為兩部分,計算出左邊區間的逆序對個數和右邊區間的個數,最后再一左一右來計算逆序對個數,在左右兩邊分別求出逆序對的個數會在遞歸過程中完成(因為遞歸到左右區間元素各為1個開始返回,兩個元素合并區間,相當于求得了各自區間的逆序對,只需考慮一左一右區間即可,如此往復),實際上只用考慮合并過程中統計出的逆序對數量。
- 升序過程
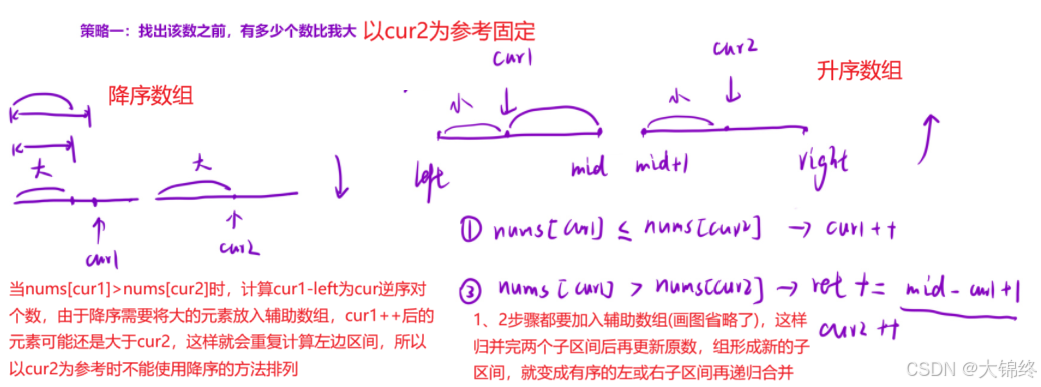
重點在遞歸合并后會形成有序的數組,以此遞歸下去,可利用數組的有序性,一次性獲得一串逆序對,如上圖中mid-cur1+1
class Solution {//輔助數組與輔助計數int num=0;vector<int> v;
public:int reversePairs(vector<int>& nums) {v.resize(nums.size());mergesort(nums,0,nums.size()-1);return num;}void mergesort(vector<int>& nums,int left,int right){if(left>=right) return ;//計算中間值int mid=(right+left)>>1;//遞歸mergesort(nums,left,mid);mergesort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=left;//歸并,處理一左一右區間的逆序對個數while(cur1<=mid&&cur2<=right){if(nums[cur1]<=nums[cur2]){v[i++]=nums[cur1++];}else {num+=(mid-cur1+1);v[i++]=nums[cur2++];}}//剩余元素處理while(cur1<=mid) v[i++]=nums[cur1++];while(cur2<=right) v[i++]=nums[cur2++];//將輔助數組中元素更新到原數組,形成新的左或右子區間遞歸for(int i=left;i<=right;i++) nums[i]=v[i];}
};
- 降序過程
//歸并,處理一左一右區間的逆序對個數while(cur1<=mid&&cur2<=right){if(nums[cur1]<=nums[cur2]){v[i++]=nums[cur2++];}else {num+=(right-cur2+1);v[i++]=nums[cur1++];}}
只有歸并這一部分不同
七. (315.) 計算右側?于當前元素的個數

解法:
思路與上一題逆序對相同,采用上題降序的思路,區別在于還需要創建一個數組來存儲原數組元素與下標的對應關系,方便返回數組更新時的下標查找,因為歸并過程讓原數組重新排序了。在歸并時除了重新排序原數組之外還要重新排序下標數組,以保持一樣的映射關系
class Solution {//定義輔助數組vector<int> tmp1;//返回值vector<int> tmp2;//下標關系//定義返回數組vector<int> ret;vector<int> index;
public:vector<int> countSmaller(vector<int>& nums) {ret.resize(nums.size());tmp1.resize(nums.size());tmp2.resize(nums.size());index.resize(nums.size());//初始化index數組為下標for(int i=0;i<nums.size();i++) index[i]=i;mergesort(nums,0,nums.size()-1);return ret;}void mergesort(vector<int>&nums,int left,int right){if(left>=right) return;//計算中間值int mid=(left+right)>>1;//遞歸處理左右子區間mergesort(nums,left,mid);mergesort(nums,mid+1,right);//歸并排序int cur1=left,cur2=mid+1;int i=left;//臨時數組下標while(cur1<=mid&&cur2<=right){if(nums[cur1]<=nums[cur2]){tmp2[i]=index[cur2];tmp1[i++]=nums[cur2++];}else{//更新返回數組,+=是因為該元素對應位置可能已經更新過了,//排序后重新計算,要用+=避免覆蓋之前結果ret[index[cur1]]+=right-cur2+1;//注意這里查找cur1的下標,因為降序數組是固定cur1,查找cur2的小于情況tmp2[i]=index[cur1];tmp1[i++]=nums[cur1++];}}//處理剩余元素while(cur1<=mid) tmp2[i]=index[cur1],tmp1[i++]=nums[cur1++];while(cur2<=right) tmp2[i]=index[cur2],tmp1[i++]=nums[cur2++];//更新原數組使之有序,并更新對應下標數組for(int i=left;i<=right;i++) nums[i]=tmp1[i],index[i]=tmp2[i];}
};
八.(493.) 翻轉對

解法:
采用計算逆序對的思路,通過升序或降序數組,利用數組有序性一次性獲得一堆符合條件的翻轉對。不同的是這里判斷條件不同,不能在歸并排序的過程中順便計算翻轉對,而是要先計算翻轉對,再進行歸并排序。
注意:
1.需要注意判斷條件不要用大于兩倍的方法,會整數溢出,用原數的一半來判斷,要/2.0保證精度判斷
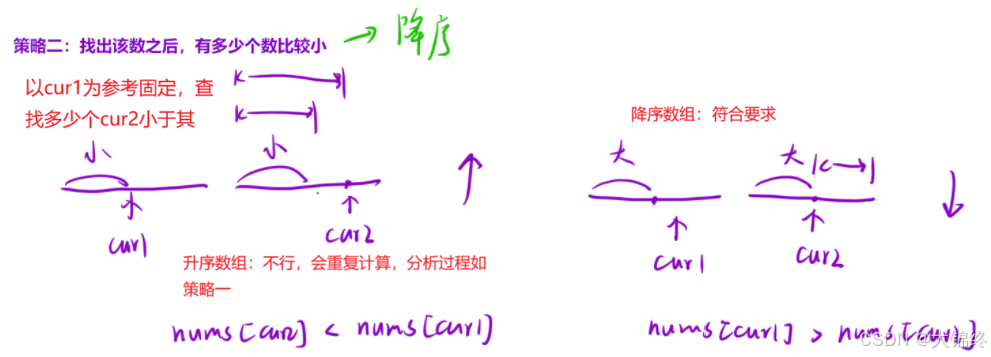
2.關于降序和升序題六中已詳解,本質是利用雙指針同向移動找出區間范圍內符合翻轉對的元素,固定一個指針再另一個指針中找符合條件的區間范圍,一般固定一側指針只能用升序數組或降序數組其中一種方法,另一種會重復計算
- 降序數組方法:
class Solution {int ret=0;vector<int> tmp;
public:int reversePairs(vector<int>& nums) {tmp.resize(nums.size());mergesort(nums,0,nums.size()-1);return ret;}void mergesort(vector<int>&nums,int left,int right){if(left>=right) return;int mid=(left+right)>>1;//遞歸計算左右兩側翻轉對數量mergesort(nums,left,mid);mergesort(nums,mid+1,right);//先計算翻轉對降序方法固定cur1,有多少個cur2小于int cur1=left,cur2=mid+1,i=left;while(cur1<=mid&&cur2<=right){if((nums[cur1]/2.0)>nums[cur2]){ret+=right-cur2+1;cur1++;}else cur2++;}//再歸并排序cur1=left,cur2=mid+1,i=left;;while(cur1<=mid&&cur2<=right){if(nums[cur1]>nums[cur2]){tmp[i++]=nums[cur1++];}else tmp[i++]=nums[cur2++];}//處理剩余元素while(cur1<=mid) tmp[i++]=nums[cur1++];while(cur2<=right) tmp[i++]=nums[cur2++];//使原數組有序,進行下次遞歸for(int i=left;i<=right;i++) nums[i]=tmp[i];}
};
- 升序數組方法
只有這一部分與降序不同,注意兩數倍數大小關系比較邏輯不變
//先計算翻轉對,升序方法固定cur2,有多少個cur1大于int cur1=left,cur2=mid+1,i=left;while(cur1<=mid&&cur2<=right){if((nums[cur1]/2.0)>nums[cur2]){ret+=mid-cur1+1;cur2++;}else cur1++;}//再歸并排序cur1=left,cur2=mid+1,i=left;;while(cur1<=mid&&cur2<=right){if(nums[cur1]>nums[cur2]){tmp[i++]=nums[cur2++];}else tmp[i++]=nums[cur1++];}
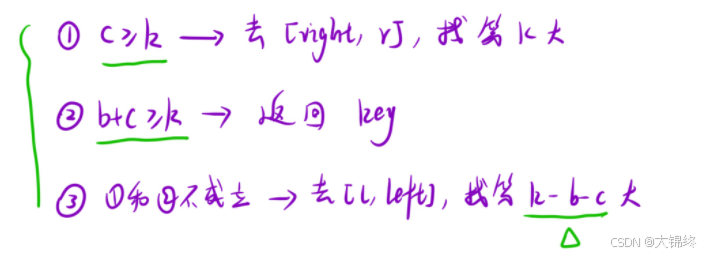

![[Linux]學習筆記系列 -- mm/page_alloc](http://pic.xiahunao.cn/[Linux]學習筆記系列 -- mm/page_alloc)





` 和 `unlock()` 線程同步函數)

![ADB 調試工具的學習[特殊字符]](http://pic.xiahunao.cn/ADB 調試工具的學習[特殊字符])










