鏈接：https://docs.e3nn.org/en/latest/examples/examples.html

---

docs：e3nn

e3nn是一個用于構建歐幾里得(E(3))等變神經網絡的Python庫，這意味著它們能自動保持三維旋轉和反射的對稱性。

該庫使用不可約表示(Irreps)來描述數據變換方式，通過張量積以原則性的方式組合這些對稱特征。

此外，該庫還利用球諧函數處理方向性數據，提供專門的等變神經網絡模塊（如線性層和激活函數），包含用于穩定訓練的歸一化策略，并支持TorchScript JIT以實現優化部署。

可視化

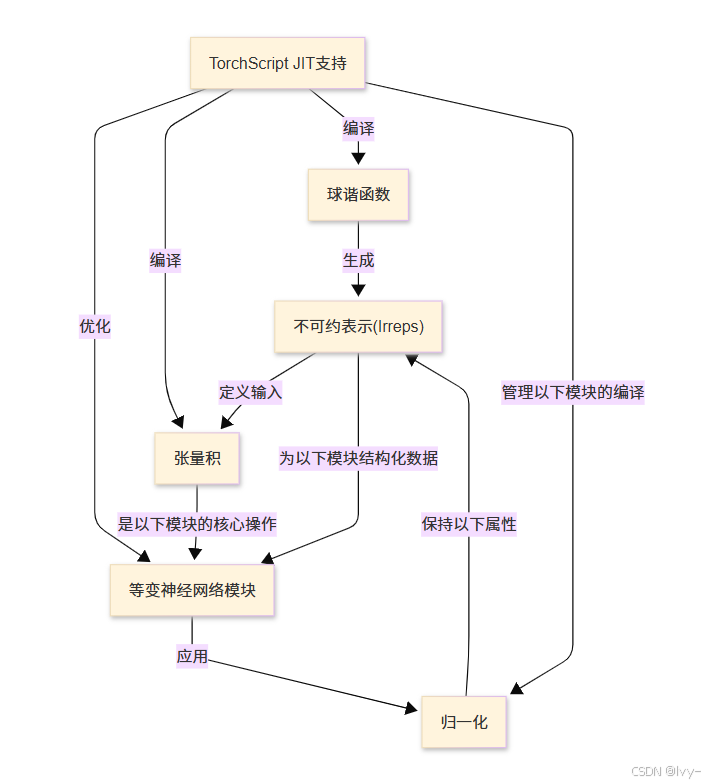
章節列表

1. 不可約表示(Irreps)
2. 球諧函數
3. 張量積
4. 等變神經網絡模塊
5. 歸一化
6. TorchScript JIT支持

---

e3nn庫文檔

該庫旨在幫助 開發E(3)等變神經網絡，包含張量積和球諧函數等基礎數學運算。

快速入門

import torch
from e3nn import o3# 創建由標量(0e)和向量(1o)組成的隨機數組
irreps_in = o3.Irreps("0e + 1o")
x = irreps_in.randn(-1)# 應用線性層
irreps_out = o3.Irreps("2x0e + 2x1o")
linear = o3.Linear(irreps_in=irreps_in, irreps_out=irreps_out)
y = linear(x)# 計算自張量積
tp = o3.FullTensorProduct(irreps_in1=irreps_in, irreps_in2=irreps_in)
z = tp(x, x)# 可選：編譯張量積運算
tp_pt2 = torch.compile(tp, fullgraph=True)
z_pt2 = tp_pt2(x, x)  # 注意：由于編譯過程，前幾次調用可能較慢
torch.testing.assert_close(z, z_pt2)

安裝指南

重要提示：請先安裝PyTorch，再執行以下命令

pip install --upgrade pip
pip install --upgrade e3nn

詳細安裝說明和可選依賴項請參閱INSTALL.md文件

版本變更說明

e3nn目前處于開發階段。建議使用pip安裝。主分支被視為不穩定版本。當代碼發生破壞性變更時，次版本號會遞增。

版本號格式：
0.(破壞性變更時遞增).(兼容性更新時遞增)

---

第1章：不可約表示(Irreps)

歡迎來到e3nn的精彩世界🐻???

這個庫能幫助我們構建對三維空間中物體行為"有認知"的神經網絡，特別是在物體旋轉或反射時。

• 想象訓練一個神經網絡來理解分子。

• 當你旋轉一個分子時，它仍然是同一個分子！

• 真正智能的網絡應該能識別這一點，而無需展示所有可能的旋轉。

這種特性被稱為**等變性**，而e3nn使之成為可能。

e3nn的核心是一個稱為不可約表示(簡稱Irreps)的基本概念。

• 可以將Irreps視為標簽，告訴e3nn你的數據代表哪種物理量。

• 這個標簽至關重要，因為它決定了當三維世界旋轉或反射時，數據應如何表現。

讓我們從一個簡單例子開始。假設你有一個球的兩條信息：

1. 溫度：這是一個單一數字。旋轉球時，其溫度(比如在中心點)不會改變。
2. 位置處的風向和風速：這是一個矢量，既有大小又有方向。旋轉球時，風矢量會隨之改變旋轉。

溫度(標量)和風(矢量)在旋轉下的表現不同。e3nn需要知道這種差異來構建等變神經網絡。這正是Irreps提供的功能

什么是Irrep(單數)？

一個Irrep(發音為"ear-rep")描述一種基本的信息"類型"或"類別"，是最小的構建模塊。

每個Irrep由兩個關鍵屬性定義：

1. l(角動量/階數)：這是一個非負整數(0,1,2,…)

   • l=0：表示標量。如溫度示例，標量是旋轉坐標系時不變的單一數字。
   • l=1：表示矢量。如風示例，矢量有方向和大小，會隨物體旋轉。
   • l=2及以上：表示更復雜的量，有時稱為張量或多極子，在旋轉下以特定方式變換。

   階數為l的Irrep維度總是2l + 1。因此標量(l=0)維度為1，矢量(l=1)維度為3。

2. p(宇稱)：取值為+1(偶，記作’e’)或-1(奇，記作’o’)。宇稱描述數據在反射(如鏡面反射)時的行為：

   • 偶宇稱(e)：反射后數據保持不變。標量溫度(0e)具有偶宇稱。
   • 奇宇稱(o)：反射后數據符號或方向翻轉。矢量(1o)具有奇宇稱——如果反射一個指向右側的矢量，它將指向左側(其分量符號翻轉)。

e3nn使用簡潔的字符串表示法。例如：

• 0e：偶宇稱標量(l=0)
• 1o：奇宇稱矢量(l=1)，這是表示3D矢量的標準方式
• 2e：偶宇稱張量(l=2)

可以在e3nn中這樣創建Irrep對象：

from e3nn.o3 import Irrep# 標量(l=0, 偶宇稱)
scalar_irrep = Irrep("0e")
print(f"標量Irrep: {scalar_irrep}, l={scalar_irrep.l}, p={scalar_irrep.p}, 維度={scalar_irrep.dim}")# 矢量(l=1, 奇宇稱)
vector_irrep = Irrep("1o")
print(f"矢量Irrep: {vector_irrep}, l={vector_irrep.l}, p={vector_irrep.p}, 維度={vector_irrep.dim}")

輸出：

標量Irrep: 0e, l=0, p=1, 維度=1
矢量Irrep: 1o, l=1, p=-1, 維度=3

什么是Irreps(復數)？

現實世界的數據通常不是單一標量或矢量，而是不同類型信息的組合。

例如空間中的一個點可能同時具有溫度(標量)和速度(矢量)。

這時就需要Irreps(復數)。Irreps對象描述多個Irrep類型的集合或直和，就像是復雜數據結構的配方。

Irreps的字符串表示法組合了單個Irrep字符串，通常帶有"多重性"數字表示特定Irrep類型出現的次數：

• 1x0e：一個標量(單實例時1x可省略)
• 2x0e：兩個獨立標量
• 0e + 1o：一個標量和一個矢量
• 3x0e + 5x1o + 2x2e： 三個標量、五個矢量和兩個l=2偶宇稱張量

創建Irreps對象的方式：

from e3nn.o3 import Irreps# 一個標量和一個矢量的組合
my_irreps = Irreps("0e + 1o")
print(f"我的Irreps: {my_irreps}")
print(f"總維度: {my_irreps.dim}")# 更復雜的組合
complex_irreps = Irreps("2x0e + 1x1o + 1x2e")
print(f"復雜Irreps: {complex_irreps}")
print(f"總維度: {complex_irreps.dim}")

輸出：

我的Irreps: 1x0e+1x1o
總維度: 4
復雜Irreps: 2x0e+1x1o+1x2e
總維度: 9

注意complex_irreps的總維度計算為：
(2 * (2*0 + 1))(兩個0e標量) +
(1 * (2*1 + 1))(一個1o矢量) +
(1 * (2*2 + 1))(一個2e張量) =
(2 * 1) + (1 * 3) + (1 * 5) = 2 + 3 + 5 = 10。

e3nn如何使用Irreps

Irreps對象本質上是數據在e3nn神經網絡中流動的藍圖。

當在e3nn中定義層時，需要指定其輸入和輸出的Irreps。

以下是e3nnREADME中的示例：

import torch
from e3nn import o3# 定義輸入數據的Irreps：一個標量和一個矢量的組合
irreps_in = o3.Irreps("0e + 1o")
print(f"輸入Irreps: {irreps_in}")# 創建符合這些Irreps的隨機輸入數據
x = irreps_in.randn(10, -1) # 10個樣本，-1會被替換為irreps_in.dim(4)
print(f"輸入數據形狀: {x.shape}")# 定義輸出數據的Irreps：兩個標量和兩個矢量的組合
irreps_out = o3.Irreps("2x0e + 2x1o")
print(f"輸出Irreps: {irreps_out}")# 創建將'irreps_in'數據轉換為'irreps_out'數據的線性層
# e3nn確保該層保持旋轉/反射等變性
linear = o3.Linear(irreps_in=irreps_in, irreps_out=irreps_out)
print(f"創建的線性層: {linear}")# 將線性層應用于輸入數據
y = linear(x)
print(f"輸出數據形狀: {y.shape}")

輸出：

輸入Irreps: 1x0e+1x1o
輸入數據形狀: torch.Size([10, 4])
輸出Irreps: 2x0e+2x1o
創建的線性層: Linear(1x0e+1x1o -> 2x0e+2x1o)
輸出數據形狀: torch.Size([10, 8])

注意o3.Linear以irreps_in和irreps_out為參數。

這告訴層如何解釋其輸入以及應產生何種輸出，同時保持等變性。

內部機制：Irreps的結構

快速了解e3nn如何存儲這些Irrep和Irreps對象：

classDiagramdirection LRclass Irrep {+int l+int p+dim: int}class _MulIr {+int mul+Irrep ir+dim: int}class Irreps {+tuple[tuple] internal_structure+dim: int+num_irreps: int}Irreps "1" * "0..*" _MulIr_MulIr "1" * "1" Irrepnote for Irrep: 表示單個不可約表示(如1o)note for _MulIr: 將多重性與Irrep結合(如2x0e)note for Irreps: _MulIr對象的集合(直和)(如2x0e+1x1o)

1. Irrep：存儲為包含(l, p)的簡單tuple。例如Irrep("1o")內部是(1, -1)，其dim屬性計算為2l+1。
2. _MulIr：另一個簡單tuple，包含(多重性, Irrep_object)。所以2x0e會是(2, Irrep(0, 1))，其dim計算為多重性 * Irrep_object.dim。
3. Irreps：_MulIr對象的tuple。當給出字符串如Irreps("2x0e + 1x1o")時，它會解析字符串，創建_MulIr(2, Irrep(0, 1))和_MulIr(1, Irrep(1, -1))，并將它們存儲在元組中。其dim屬性是所有_MulIr組件維度的總和。

當要求Irreps對象提供其變換矩陣(如通過irreps.D_from_matrix(R))時，e3nn會為每個單獨的Irrep計算變換矩陣(使用稱為wigner_D的函數，我們將在下一章詳細介紹)，然后將它們組合成一個大的塊對角矩陣。這種塊對角結構意味著每種Irrep類型獨立變換，這是不可約表示的關鍵特性。

Irrep與Irreps快速對比

特性	Irrep(單數)	Irreps(復數)
概念	單一基本的數據變換類型	多個Irrep類型的集合或"直和"
屬性	l(階數)和p(宇稱)	(多重性, Irrep)對的列表
示例	0e(標量), 1o(矢量)	2x0e + 1o(兩個標量和一個矢量)
維度	2l + 1	所有組件的多重性 * (2l + 1)之和
用途	定義單個組件	定義e3nn中數據的整體結構

結論

本章中，我們了解到Irreps是e3nn中描述數據(如標量或矢量)在旋轉和反射下行為的基本"標簽"。這種理解對于構建等變神經網絡至關重要，這些網絡本質上尊重3D空間的對稱性。我們學習了如何創建Irrep和Irreps對象，以及e3nn如何使用它們來定義其層的輸入和輸出類型。

下一章中，我們將深入探討這些Irreps如何通過球諧函數在3D空間中數學表示，這些函數是表達這些旋轉和反射場的"基"。

第2章：球諧函數

---

e3nn 概述

e3nn 是一個用于構建歐幾里得等變神經網絡（E(3)-equivariant neural networks）的 Python 庫，能夠自動保持三維旋轉和反射的對稱性。

該庫通過不可約表示（Irreps）描述數據變換方式，利用球諧函數處理方向性數據，并提供專門的等變神經網絡模塊。

核心功能

基于不可約表示的數據描述系統

• 使用 Irreps 定義數據類型（如標量 0e、矢量 1o）
• 支持組合多種數據類型（如 "0e + 1o" 表示標量和矢量組合）

基礎數學運算

• 張量積運算
• 球諧函數處理

神經網絡組件

• 等變線性層
• 歸一化策略
• TorchScript JIT 支持

應用示例:

• 分子性質預測
• 3D 點云處理

前文傳送：[GICP] 點云數據結構 | 點云配準 | KD樹 | 常見樹狀搜索結構

安裝與版本

• 安裝簡單，但需先安裝 PyTorch
• 該庫使用版本號 0.X.Y 格式，次版本號遞增表示破壞性變更