目錄
一、Apriori算法核心原理
1. 基本概念
2. Apriori性質
二、完整案例計算(超市購物數據)
?步驟1:按字母序重排每筆交易?
?步驟2:統計頻繁1-項集(min_support=40%)??
?步驟3:生成候選2-項集?
?步驟4:生成候選3-項集?
?步驟5:生成關聯規則(min_conf=60%)??
(1)從頻繁2-項集生成規則
(2)篩選有效規則(Conf≥60%且Lift>1)
(3)?最終強關聯規則?
?關鍵結論?
三、Python實現代碼
四、算法特性總結
五、面試常見問題
六、例題
題目1
題目2
七、面試題
一、基礎概念題
二、流程與實現題
三、優缺點與優化題
四、實戰應用題
一、Apriori算法核心原理
1. 基本概念
-
?頻繁項集?:經常一起出現的物品組合(如{啤酒,尿布})
-
?支持度(Support)??:項集出現的頻率
Support(X) = 包含X的交易數 / 總交易數 -
?置信度(Confidence)??:規則X→Y的可靠性
Confidence(X→Y) = Support(X∪Y) / Support(X) -
?提升度(Lift)??:X對Y的促進效果
Lift(X→Y) = Support(X∪Y) / (Support(X)*Support(Y))
2. Apriori性質
?關鍵定理?:若項集是頻繁的,則其所有子集也一定是頻繁的
(反之:若子集不頻繁,則超集一定不頻繁)
二、完整案例計算(超市購物數據)
原始數據(5筆交易):
商品字母順序:啤酒(B) < 黃油(H) < 雞蛋(J) ?< 面包(M) < 牛奶(N)?
| 交易ID | 商品組合 |
|---|---|
| 1 | 牛奶, 面包, 雞蛋 |
| 2 | 牛奶, 啤酒 |
| 3 | 面包, 黃油 |
| 4 | 牛奶, 面包, 啤酒 |
| 5 | 面包, 黃油 |
?參數設置?:最小支持度=40%(至少出現2次),最小置信度=60%
?步驟1:按字母序重排每筆交易?
| 交易ID | 原始商品組合 | 排序后商品組合(按B<H<J<M<N) |
|---|---|---|
| 1 | 牛奶,面包,雞蛋 | ?雞蛋(J), 面包(M), 牛奶(N)?? |
| 2 | 牛奶,啤酒 | ?啤酒(B), 牛奶(N)?? |
| 3 | 面包,黃油 | ?黃油(H), 面包(M)?? |
| 4 | 牛奶,面包,啤酒 | ?啤酒(B), 面包(M), 牛奶(N)?? |
| 5 | 面包,黃油 | ?黃油(H), 面包(M)?? |
?關鍵點?:字母順序優先級:B(啤酒) → H(黃油) → J(雞蛋) → M(面包) → N(牛奶)
?步驟2:統計頻繁1-項集(min_support=40%)??
| 商品 | 出現次數 | 支持度 | 是否頻繁 |
|---|---|---|---|
| 啤酒 | 2 | 2/5=40% | ? |
| 黃油 | 2 | 2/5=40% | ? |
| 雞蛋 | 1 | 1/5=20% | ? |
| 面包 | 4 | 4/5=80% | ? |
| 牛奶 | 3 | 3/5=60% | ? |
?頻繁1-項集?:{'啤酒'}, {'黃油'}, {'面包'}, {'牛奶'}
(排除{'雞蛋'},因支持度20% < 40%)
?步驟3:生成候選2-項集?
連接頻繁1-項集(按字母序組合):
| 候選2-項集 | 出現交易ID | 支持度 | 是否頻繁 |
|---|---|---|---|
| {啤酒,黃油} | 無 | 0% | ? |
| {啤酒,面包} | 4 | 1/5=20% | ? |
| {啤酒,牛奶} | 2,4 | 2/5=40% | ? |
| {黃油,面包} | 3,5 | 2/5=40% | ? |
| {黃油,牛奶} | 無 | 0% | ? |
| {面包,牛奶} | 1,4 | 2/5=40% | ? |
?頻繁2-項集?:{'啤酒', '牛奶'}, {'黃油', '面包'}, {'面包', '牛奶'}
?步驟4:生成候選3-項集?
嘗試連接頻繁2-項集(需前k-2=1項相同):
-
{'啤酒','牛奶'} + {'面包','牛奶'} → 前1項'啤酒'≠'面包' → ?無法連接?
-
其他組合均不滿足前1項相同條件
?無候選3-項集生成?
?步驟5:生成關聯規則(min_conf=60%)??
(1)從頻繁2-項集生成規則
-
??{'啤酒', '牛奶'}?:
-
規則1:啤酒 → 牛奶
Conf = Support(啤酒,牛奶)/Support(啤酒) = 0.4/0.4 = ?100%??
Lift = 0.4/(0.4 * 0.6) ≈ ?1.67?
-
規則2:牛奶 → 啤酒
Conf = 0.4/0.6 ≈ ?66.7%??
Lift ≈ 1.67
-
-
??{'黃油', '面包'}?:
-
規則3:黃油 → 面包
Conf = 0.4/0.4 = ?100%??
Lift = 0.4/(0.4 * 0.8) = ?1.25?
-
規則4:面包 → 黃油
Conf = 0.4/0.8 = ?50%??
Lift = 1.25
-
-
??{'面包', '牛奶'}?:
-
規則5:面包 → 牛奶
Conf = 0.4/0.8 = ?50%??
Lift = 0.4/(0.8 * 0.6) ≈ ?0.83?
-
規則6:牛奶 → 面包
Conf = 0.4/0.6 ≈ ?66.7%??
Lift ≈ 0.83
-
(2)篩選有效規則(Conf≥60%且Lift>1)
| 規則 | 置信度 | 提升度 | 是否有效 |
|---|---|---|---|
| 啤酒 → 牛奶 | 100% | 1.67 | ? |
| 牛奶 → 啤酒 | 66.7% | 1.67 | ? |
| 黃油 → 面包 | 100% | 1.25 | ? |
| 面包 → 黃油 | 50% | 1.25 | ? |
| 面包 → 牛奶 | 50% | 0.83 | ? |
| 牛奶 → 面包 | 66.7% | 0.83 | ? |
(3)?最終強關聯規則?
-
?啤酒 → 牛奶?(買啤酒的顧客100%會買牛奶,且概率是普通顧客的1.67倍)
-
?牛奶 → 啤酒?(買牛奶的顧客66.7%會買啤酒,概率是普通顧客的1.67倍)
-
?黃油 → 面包?(買黃油的顧客100%會買面包,概率是普通顧客的1.25倍)
?關鍵結論?
-
?字母序的嚴格性?:確保所有項集按固定順序處理(如{啤酒,牛奶}不會與{牛奶,啤酒}重復)
-
?商業價值最高的規則?:啤酒與牛奶的強雙向關聯(提升度1.67),可設計組合促銷
-
?面包的高頻性?:因面包本身支持度高(80%),導致與黃油的規則提升度較低(1.25)
三、Python實現代碼
import pandas as pd
from mlxtend.frequent_patterns import apriori
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import association_rulesitemSetList = [['牛奶', '面包', '雞蛋'],['啤酒', '牛奶'],['黃油', '面包'],['啤酒', '面包', '牛奶'],['黃油', '面包']
]#數據預處理——編碼
te = TransactionEncoder()
te_array = te.fit(itemSetList).transform(itemSetList)
df = pd.DataFrame(te_array, columns = te.columns_)#挖掘頻繁項集(最小支持度為0.5)
frequent_itemsets = apriori(df, min_support = 0.4, use_colnames = True)
print("發現的頻繁項集包括:\n")
frequent_itemsets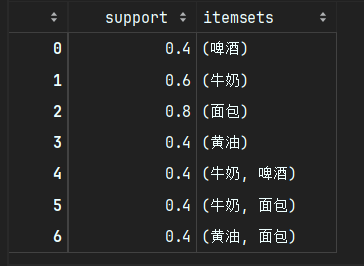
-
TransactionEncoder()將購物籃數據轉換為機器學習算法可處理的格式 -
fit()學習數據中所有唯一的商品項 -
transform()將每個購物籃轉換為布爾向量(出現=True,未出現=False) -
最終生成的數據框
df如下:
| 牛奶 | 面包 | 雞蛋 | 啤酒 | 薯片 | |
|---|---|---|---|---|---|
| 0 | True | True | True | False | False |
| 1 | False | True | False | True | True |
| 2 | True | True | False | True | True |
| 3 | False | False | False | True | True |
-
apriori()函數執行Apriori算法 -
min_support=0.5表示只保留出現頻率≥50%的項集 -
use_colnames=True使用商品名稱而非列索引作為輸出
rules = association_rules(frequent_itemsets, metric = 'confidence', min_threshold = 0.6, support_only = False)rules= rules[ rules['lift']>1]
print("生成的強關聯規則為:\n")
rules
association_rules()函數從頻繁項集中生成關聯規則,參數說明:
-
frequent_itemsets: 之前通過apriori()找到的頻繁項集 -
metric='confidence': 使用置信度作為主要評估指標 -
min_threshold=0.5: 只保留置信度≥50%的規則 -
support_only=False: 計算所有指標(不只計算支持度)
rules[rules['lift']>1]只保留提升度(lift)大于1的規則,這表示:
-
規則前項和后項是正相關的
-
前項的出現確實會提高后項出現的概率
關鍵指標解釋
-
?antecedents? (前項) → ?consequents? (后項):
-
規則形式:如果買了前項商品,那么也可能買后項商品
-
-
?support? (支持度):
-
規則在所有交易中出現的頻率
-
例如"啤酒→薯片"支持度0.5表示這兩個商品一起出現在50%的交易中
-
-
?confidence? (置信度):
-
當前項出現時,后項也出現的概率
-
"啤酒→薯片"置信度0.67表示買了啤酒的顧客中,67%也買了薯片
-
-
?lift? (提升度):
-
衡量前項對后項的提升效果
-
lift>1表示正相關(一起購買的可能性比隨機更高)
-
lift=1表示獨立
-
lift<1表示負相關
-
四、算法特性總結
| 特性 | 說明 |
|---|---|
| ?優點? | 邏輯簡單直觀,適合教學 |
| ?缺點? | 需多次掃描數據庫,效率較低 |
| ?適用場景? | 中小規模數據集 |
| ?改進算法? | FP-Growth(只需掃描2次數據庫) |
| ?商業應用? | 購物籃分析、交叉銷售推薦 |
五、面試常見問題
-
?為什么Apriori需要多次掃描數據庫???
每輪迭代都需要重新計算候選項集的支持度計數。
-
?如何判斷一個規則是否有價值???
綜合看支持度(覆蓋率)、置信度(可靠性)和提升度(相關性)。
-
?提升度=1意味著什么???
表示前項和后項獨立出現,沒有關聯關系。
-
?如何處理數值型數據???
需要先離散化(如將年齡分為"青年/中年/老年")。
六、例題
題目1

題目問的是:??"關聯規則挖掘方法是一種基于規則的機器學習算法,以下關于關聯規則挖掘方法的描述錯誤的是()"?。
選項解析
?選項A?:
"生產關聯規則一般利用最小支持度從數據庫中找到頻繁項集"
- ?正確?:關聯規則挖掘的第一步是通過最小支持度(min_support)?篩選出頻繁項集(Frequent Itemsets)。
- 例如,如果{牛奶,面包}在交易數據中出現的頻率 ≥ min_support,則它是一個頻繁項集。
?選項B?:
"生成關聯規則一般利用最小置信度從頻繁項集中找到關聯規則"
- ?正確?:在得到頻繁項集后,通過最小置信度(min_confidence)?生成關聯規則。
- 例如,從{牛奶,面包}可能生成規則"牛奶→面包",其置信度 = P(面包|牛奶) ≥ min_confidence。
?選項C?:
"關聯規則挖掘屬于有監督學習算法"
- ?錯誤?(正確答案):關聯規則挖掘是典型的無監督學習方法。
- ?原因?:它不需要預先標注的標簽(如分類問題中的類別),而是直接從數據中探索項之間的關聯性。
- 有監督學習需要明確的輸入-輸出對(如分類、回歸),而關聯規則僅分析數據內在模式。
?選項D?:
"如果一個項集是頻繁的,那么它的所有子集也一定是頻繁的"
- ?正確?:這是Apriori算法的核心性質(反單調性)。
- 例如,若{牛奶,面包,啤酒}是頻繁的,則{牛奶,面包}、{牛奶}等子集一定也是頻繁的(因為子集的支持度 ≥ 父項集的支持度)。
關聯規則挖掘的核心概念
?頻繁項集(Frequent Itemsets)??:
- 通過最小支持度篩選出現頻率高的項組合。
- 例如,{牛奶,面包}在超市交易中經常一起購買。
?關聯規則(Association Rules)??:
- 形式:X → Y(如"買牛奶的人也會買面包")。
- 通過最小置信度篩選可靠的規則。
?無監督性?:
- 不需要預先知道"正確答案",而是自動發現數據中的模式。
題目2

正確答案與解析:C(提升度/Lift)??
?核心概念解析?
-
?支持度(Support)??:
- 衡量規則中物品組合出現的頻率?
- 公式:Support(X→Y)=P(X∪Y)
- 局限性:高支持度可能包含常識性組合(如"面包+牛奶"),無法反映相關性。
-
?置信度(Confidence)??:
- 衡量規則可靠性?(X出現時Y的概率)
- 公式:Confidence(X→Y)=P(Y∣X)
- 局限性:可能高估單向關聯(如"尿布→啤酒"置信度高,但反向不成立)。
-
?提升度(Lift)??:
- ?關鍵指標?:直接衡量X與Y的相關性強度?
- 公式:Lift=P(X)P(Y)P(X∪Y)?
- 解釋:
- =1:X與Y獨立
-
1:正相關(值越大關聯越強)
- <1:負相關
- 優勢:消除數據傾斜影響,識別真正有意義的規則。
-
?支持度置信度比?:
- 非標準指標,實際應用極少。
?為什么選C???
- ?題目要求?:"衡量強度和重要性?" → 需同時排除高頻但無意義的規則(支持度缺陷)和虛假關聯(置信度缺陷)。
- ?提升度唯一能反映:
- 規則是否比隨機組合更有價值(如Lift=3表示該規則出現概率是隨機預期的3倍)。
- 經典案例:
- 若"啤酒+尿布"的Lift遠高于1,說明組合購買行為非偶然,具有商業價值。
?對比總結?
| 指標 | 作用 | 適用場景 | 局限性 |
|---|---|---|---|
| 支持度 | 篩選高頻組合 | 商品陳列優化 | 無法評估相關性 |
| 置信度 | 評估規則可靠性 | 推薦系統(單向推薦) | 可能高估虛假關聯 |
| ?提升度? | ?量化相關性強度? | 精準營銷、交叉銷售 | 計算復雜度稍高 |
?擴展思考?
若題目改為"篩選高頻項集",則應選支持度;若問"評估規則可信度",則選置信度。
?Lift是關聯規則挖掘中唯一能同時抵抗"高頻項干擾"和"數據傾斜誤導"的指標。
七、面試題
一、基礎概念題
1. 請簡要描述 Apriori 算法是什么,以及它解決的是什么問題?
答案:
Apriori 算法是一種經典的用于關聯規則學習的算法,主要用于從大規模數據集中發現項(item)之間的有趣關系,即關聯規則。
它解決的核心問題是“購物籃分析”,例如“如果顧客購買了商品A,那么他有多大的可能也會購買商品B?”(著名的“啤酒與尿布”案例)。其目標是發現那些頻繁一起出現的物品集合(頻繁項集),并基于這些項集生成強關聯規則。
2. 解釋 Apriori 算法中的兩個核心概念:支持度(Support)和置信度(Confidence)。
答案:
-
支持度(Support):?衡量一個項集(如 {X, Y})在整個數據集中出現的頻率。它的計算公式是:
Support(X) = (包含X的交易數) / (總交易數)
支持度用于篩選“頻繁”出現的項集,過濾掉那些偶然出現的組合。 -
置信度(Confidence):?衡量在包含項集 X 的交易中,也包含項集 Y 的條件概率。對于規則 X -> Y,其計算公式是:
Confidence(X -> Y) = Support(X ∪ Y) / Support(X)
置信度用于衡量規則的可靠性。置信度越高,說明當X出現時,Y也出現的可能性越大。
3. Apriori 算法的核心思想是什么?請闡述其名字“Apriori”的含義。
答案:
Apriori 算法的核心思想是?“先驗知識”?或?“反單調性”(Apriori Principle)。
其具體內容是:如果一個項集是頻繁的,那么它的所有子集也一定是頻繁的。反之,如果一個項集是非頻繁的,那么它的所有超集也一定是非頻繁的。
“Apriori”這個名字來源于拉丁語,意為“從先前的”。在算法中,它正是指利用了這個“先驗”的性質來剪枝,大大減少需要計算的候選集數量,從而提升算法效率。例如,如果項集 {啤酒} 本身都不頻繁,那么我們根本不需要去計算更大的項集 {啤酒,尿布} 的支持度,因為它絕不可能是頻繁的。
二、流程與實現題
4. 請描述 Apriori 算法發現頻繁項集的主要步驟。
答案:
Apriori 算法采用一種逐層搜索的迭代方法,由k項集探索(k+1)項集。主要步驟如下:
-
設定最小支持度閾值(min_support):?由用戶指定,用于判斷項集是否“頻繁”。
-
掃描數據集,生成候選1項集(C?),并計算其支持度。
-
剪枝:?將支持度低于 min_support 的候選集剔除,得到頻繁1項集(L?)。
-
迭代(k>1):
a.?連接步(Join):?將頻繁(k-1)項集(L???)與自身連接,生成候選k項集(C?)。
b.?剪枝步(Prune):?利用 Apriori 原理,檢查候選k項集的所有(k-1)項子集是否都在 L??? 中。如果不是,則直接刪除該候選集(因為其子集不頻繁,它本身也不可能是頻繁的)。
c.?掃描步(Scan):?再次掃描數據集,計算修剪后剩下的候選k項集的支持度。
d.?再次剪枝:?剔除支持度低于 min_support 的候選集,得到頻繁k項集(L?)。 -
終止:?重復步驟4,直到不能再生成新的頻繁項集為止(即 C??? 為空)。
5. 在生成了所有頻繁項集后,如何從中挖掘關聯規則?
答案:
對于每一個頻繁項集 L,找出其所有的非空子集。
對于每一個非空子集 S,生成一條規則 S -> (L - S)。
計算這條規則的置信度:
Confidence(S -> (L-S)) = Support(L) / Support(S)
如果該置信度大于或等于用戶設定的最小置信度閾值(min_confidence),則保留這條規則,認為是一條強關聯規則。
三、優缺點與優化題
6. 談談 Apriori 算法的主要優點和缺點。
答案:
-
優點:
-
原理簡單:?易于理解和實現。
-
利用先驗原理剪枝:?顯著減少了需要計算的候選集數量,是它成功的關鍵。
-
-
缺點:
-
需要多次掃描數據庫:?在每一層迭代中都需要掃描一次整個數據集來計算候選集的支持度,當數據集很大時,I/O開銷巨大,是性能的主要瓶頸。
-
可能產生大量的候選集:?尤其是當存在長頻繁模式或支持度閾值設置過低時,會產生指數級數量的候選集,導致內存不足。
-
效率問題:?對于海量數據集,計算效率較低。
-
7. 針對 Apriori 算法的缺點,有哪些常見的改進或優化方案?
答案:
-
基于數據劃分(Partitioning):?將數據集劃分成多個塊,分別挖掘每個塊的頻繁項集,最后再合并結果。可以減少內存需求。
-
基于采樣(Sampling):?對原始數據集進行采樣,在小樣本上挖掘頻繁項集,然后用整個數據集驗證。犧牲一定精度來換取速度。
-
使用哈希表(Hashing):?在生成候選1項集或2項集時,使用哈希技術來更快地計數,減少比較次數。
-
動態項集計數(DIC):?在掃描的不同點添加新的候選集,而不是在每次掃描開始時決定,可以更早地剪枝。
-
采用更先進的算法:
-
FP-Growth(頻繁模式增長)算法:?這是最著名的改進算法。它只須掃描數據集兩次,將數據壓縮到一棵FP樹中,然后在樹上進行挖掘,完全不產生候選集,效率遠高于 Apriori。
-
四、實戰應用題
8. 給定一個簡單的交易數據集,請手動演示找出頻繁項集的過程。
數據集:
T1: {Milk, Bread}
T2: {Milk, Diaper, Beer, Eggs}
T3: {Bread, Diaper, Beer, Cola}
T4: {Bread, Milk, Diaper, Beer}
T5: {Bread, Milk, Diaper, Cola}
設最小支持度 min_support = 3/5 = 0.6
答案:
第一次掃描:?生成候選1項集 C? 并計算支持度。
| 項集 | Support |
|---|---|
| Milk | 4 |
| Bread | 4 |
| Diaper | 4 |
| Beer | 3 |
| Eggs | 1 |
| Cola | 2 |
剪枝:?剔除支持度 < 3 的項集(Eggs, Cola),得到頻繁1項集 L?。
L? = {Milk:4, Bread:4, Diaper:4, Beer:3}
第二次掃描:?由 L? 連接生成候選2項集 C? = L? × L?。
C? = { {Milk, Bread}, {Milk, Diaper}, {Milk, Beer}, {Bread, Diaper}, {Bread, Beer}, {Diaper, Beer} }
掃描計算 C? 支持度:
| 項集 | Support |
|---|---|
| {Milk, Bread} | 3 (出現在T1, T4, T5) |
| {Milk, Diaper} | 4 (出現在T2, T4, T5) |
| {Milk, Beer} | 2 (出現在T2, T4) |
| {Bread, Diaper} | 4 (出現在T3, T4, T5) |
| {Bread, Beer} | 2 (出現在T3, T4) |
| {Diaper, Beer} | 3 (出現在T2, T3, T4) |
剪枝:?剔除支持度 < 3 的項集({Milk, Beer}, {Bread, Beer}),得到頻繁2項集 L?。
L? = { {Milk, Bread}:3, {Milk, Diaper}:4, {Bread, Diaper}:4, {Diaper, Beer}:3 }
第三次掃描:?由 L? 連接生成候選3項集 C?。
連接:L? 中的項集兩兩連接,要求前(k-2)項相同。
{Milk, Bread} 和 {Milk, Diaper} 可連接為 {Milk, Bread, Diaper}
{Milk, Bread} 和 {Bread, Diaper} 可連接為 {Milk, Bread, Diaper} (同上)
{Milk, Diaper} 和 {Bread, Diaper} 可連接為 {Milk, Bread, Diaper} (同上)
{Milk, Diaper} 和 {Diaper, Beer} 可連接為 {Milk, Diaper, Beer}
... 等等,但需要檢查子集是否頻繁。
剪枝(Prune Step):?檢查每個候選3項集的所有2項子集是否都在 L? 中。
-
候選 {Milk, Bread, Diaper}:其子集 {Milk, Bread}, {Milk, Diaper}, {Bread, Diaper} 都在 L? 中,保留。
-
候選 {Milk, Diaper, Beer}:其子集 {Milk, Beer}?不在 L? 中(因為支持度只有2),因此刪除該候選。
-
其他候選同理判斷。最終 C? = { {Milk, Bread, Diaper} }
掃描計算 C? 支持度:
{Milk, Bread, Diaper} 出現在 T4, T5,支持度為 2。
剪枝:?支持度 2 < 3,因此 L? 為空。
算法終止。?所有頻繁項集為 L? ∪ L?。











)
小學生起點(一))
保姆級教學)





