初識 Transformer （1）

1.簡介

1.1主要特點：

self-attention：

自注意力機制，Transformer的核心是自注意力機制，它允許模型在處理某個位置的輸入時，能夠直接與其他位置的輸入交互，而不像CNN、RNN只能順序處理數據。自注意力機制通過計算輸入序列中各位置之間的相似度來決定各位置之間的影響力，從而提高了模型的表現力。

并行化能力

由于Transformer不依賴于序列的順序處理，它的計算過程可以并行化，這就可以顯著提高了訓練效率。

Encoder-Decoder

Transformer 采用了典型的編碼器-解碼器架構。編碼器負責處理輸入序列，將其轉換為上下文相關的表示；解碼器則根據這些表示生成輸出序列。

1.2. 模型結構

Transformer主要由編碼器（Encoder）和解碼器（Decoder）組成，廣泛應用于自然語言處理任務，尤其是機器翻譯。

—

2.代碼實現

2.1 輸入序列

輸入是一個序列，如詞向量序列，假設：
$$X=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^{n\times d}$$
是 $n$ 個輸入，$d$ 是輸入維度，則自注意力的目的是捕獲 $n$ 個實體之間的關系。

  #定義一個詞表vocab={"我","是","一個","好","人"}

2.2 詞語關系

it代表的是animal還是street呢，對我們來說簡單，但對機器來說是很難判斷的。self-attention就能夠讓機器把it和animal聯系起來。

2.3 線性變換

自注意力機制依賴于三個核心概念：查詢向量Query、鍵向量Key、值向量Value。他們對輸入 $X$ 進行三次線性變換，得到三個矩陣。

#詞嵌入向量num_embedding=len(vocab)embedding=nn.Embdedding(num_embedding,256)#詞嵌入，傳入詞表大小和詞嵌入維度（特征維度）#獲取“我的”的詞向量embed=embedding(torch.Tensor([0]))#映射一個query向量Q=nn.Linear(256,4)(embed)#映射一個key向量K=nn.Linear(256,4)(embed)#映射一個value向量V=nn.Linear(256,4)(embed)

2.3.1 查詢向量

Q = Query, 是自注意力機制中的“詢問者”。每個輸入都會生成一個查詢向量，表示當前詞的需求。

• 作用：用于與鍵向量計算相似度（通過點積方式），確定當前詞與其他詞的相關性。
• 生成方式：通過一個權重矩陣將輸入數據（如詞向量）映射到查詢空間。

$$Q=X{W}_q$$

$W_q$ 是可學習權重矩陣，維度為 $d\times d_k$，$d_k$是超參數，表示查詢向量的維度。

2.3.2 鍵向量

**K = **Key，表示其他詞的信息，供查詢向量匹配。每個輸入都會生成一個鍵向量，表示其能夠提供的信息內容。

• 作用：與查詢向量計算點積，生成注意力權重。點積越大，表示它們之間的相關性越強。
• 生成方式：通過一個權重矩陣將輸入數據（如詞向量）映射到鍵空間。

$$K=X{W}_k$$

$W_k$ 是可學習權重矩陣，維度為 $d\times d_k$，$d_k$是超參數，表示鍵向量的維度。

2.3.3 值向量

V = Value, 值向量包含了每個輸入實際的信息內容，相關性決定了信息被聚焦的程度。

• 作用：使用值向量基于注意力得分進行加權求和，生成最終的輸出表示。
• 生成方式：通過一個權重矩陣將輸入數據（如詞向量）映射到值空間。

$$V=X{W}_v$$

$W_v$ 是可學習權重矩陣，維度為 $d\times d_v$，$d_v$是超參數，表示值向量的維度。

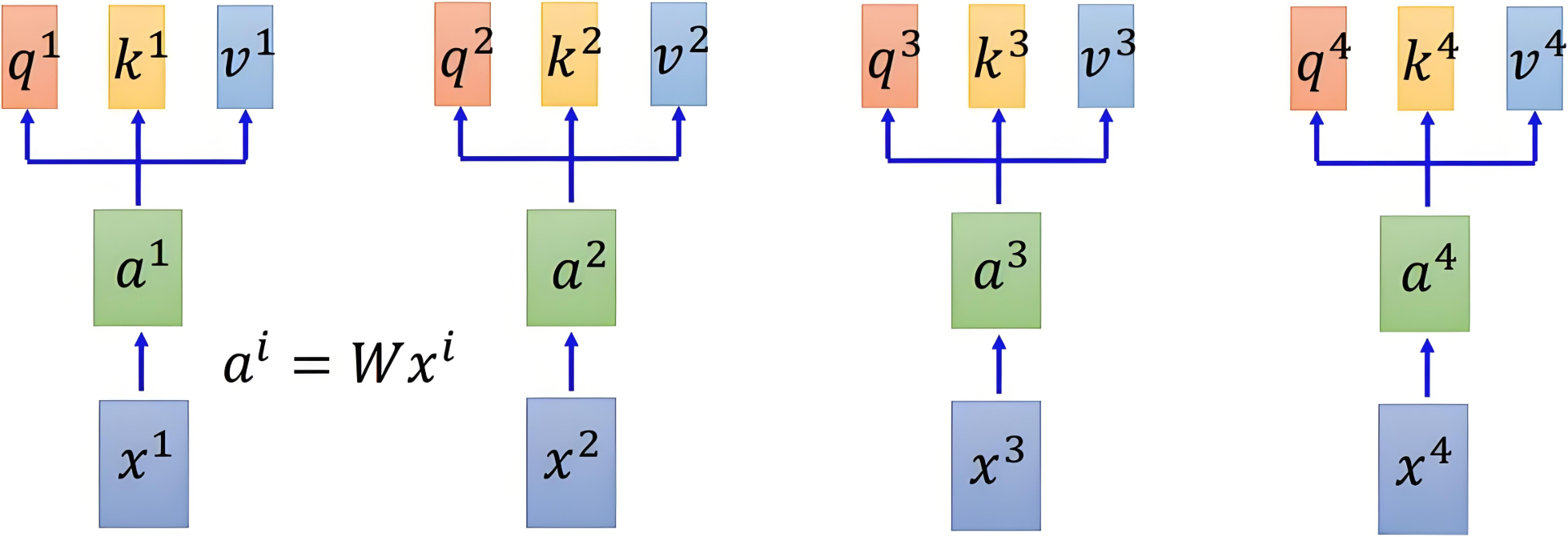
2.3.4 以圖示意

通過線性變換得到三個向量的變化如下圖所示：

2.4 注意力得分

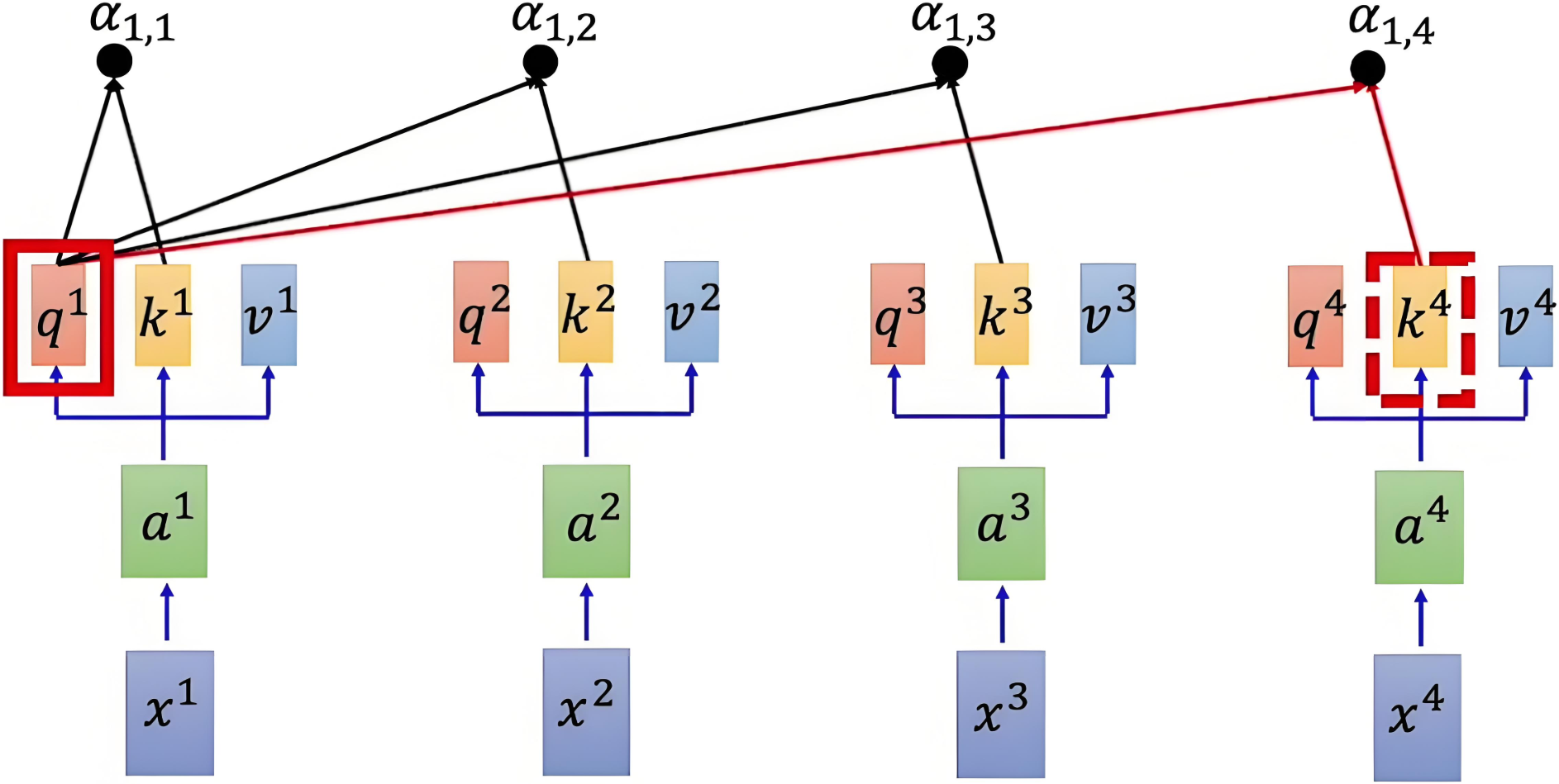
使用點積來計算查詢向量和鍵向量之間的相似度，除以縮放因子 $\sqrt{d_k}$ 來避免數值過大，使得梯度穩定更新。得到注意力得分矩陣：
$$\text{Attention}(Q,K)=\frac{Q{K}^T}{\sqrt{d_k}}$$
注意力得分矩陣維度是 $n\times n$，其中 $n$ 是序列的長度。每個元素 $(i,j)$ 表示第 $i$ 個元素與第 $j$ 個元素之間的相似度。

參考示意圖如下：

   fc = nn.ModuleList(nn.Linear(dim, dim) for _ in range(3))Q = fc[0](sentence_embedding)K = fc[1](sentence_embedding)V = fc[2](sentence_embedding)# print(Q.shape, K.shape, V.shape)# 余弦相似度  []# "I Love Nature Language Processing"sim = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(dim)# print('原始得分：',sim)

.5 歸一化

為了將注意力得分轉換為概率分布，需按行對得分矩陣進行 $softmax$ 操作，確保每行的和為 1，得到的矩陣表示每個元素對其他元素的注意力權重。是的，包括自己。
$$\text{Attention?Weight}=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$$

具體到每行的公式如下：
$${\hat{\alpha }}_{1,i}=\frac{\exp ({\alpha }_{1,i})}{{\sum }_j\exp ({\alpha }_{1,j})}$$

• ${\alpha }_{1,i}$ ：第 $1$ 個詞語和第 $i$ 個詞語之間的原始注意力得分。
• ${\hat{\alpha }}_{1,i}$ ：經過歸一化后的注意力得分。

    score = F.softmax(sim, dim=-1)# print('歸一化操作：', score)

2.6 加權求和

通過將注意力權重矩陣與值矩陣 $V$ 相乘，得到加權的值表示。
$$\text{Output}=\text{Attention?Weight}\times V=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)\times V$$

   # 加權求和：我（一開始的詞向量）不再是我(通過上下文進行加權求和之后的我)output = torch.matmul(score, V)print( output[0])

具體計算示意圖如下：

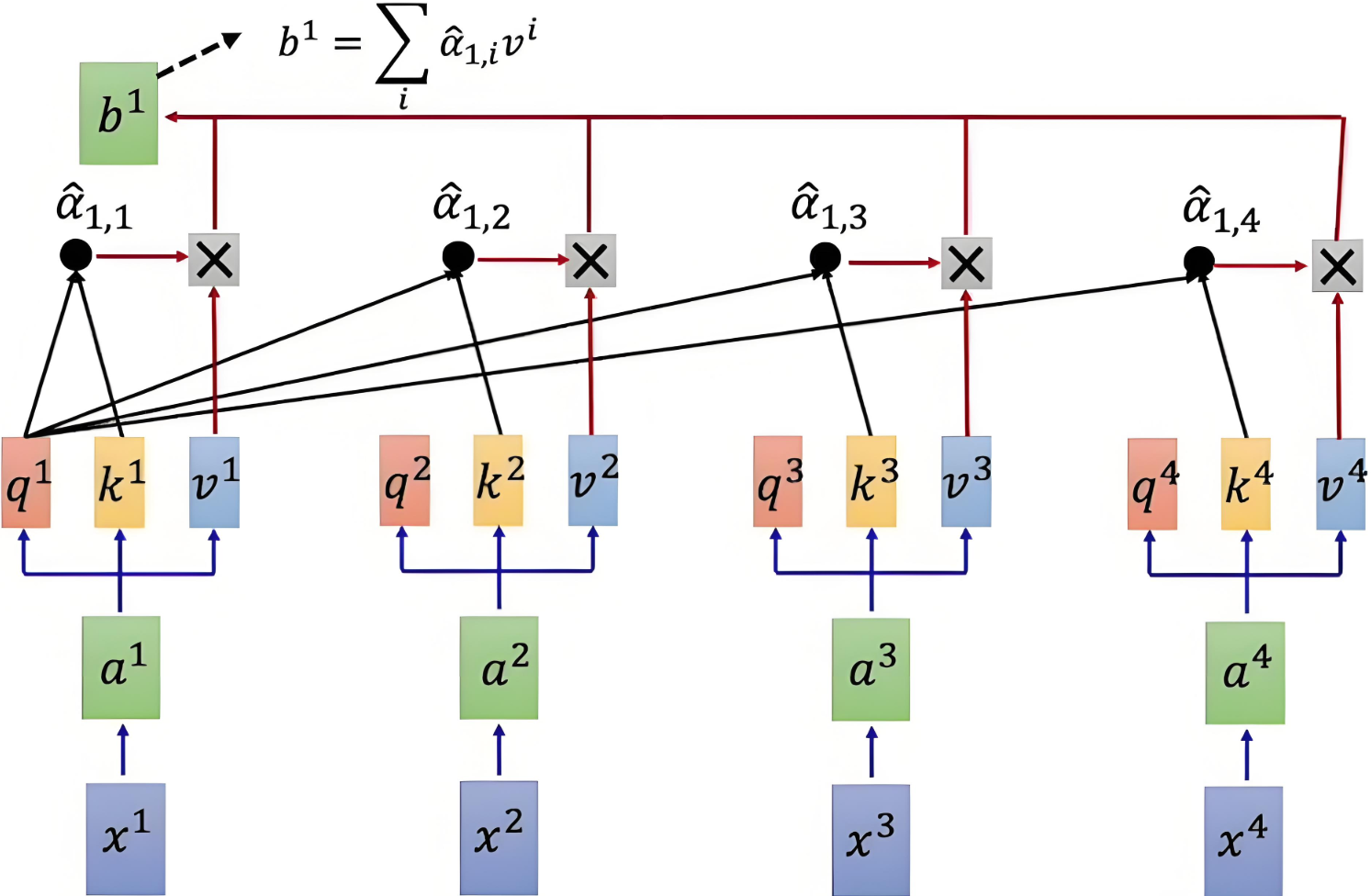
| Q和K計算相似度后，經 $softmax$ 得到注意力，再乘V，最后相加得到包含注意力的輸出 |

3. 多頭注意力機制

Multi-Head Attention，多頭注意力機制，是對自注意力機制的擴展。

3.1 基本概念

多頭注意力機制的核心思想是，將注意力機制中的 $Q、K、V$ 分成多個頭，每個頭計算出獨立的注意力結果，然后將所有頭的輸出拼接起來，最后通過一個線性變換得到最終的輸出。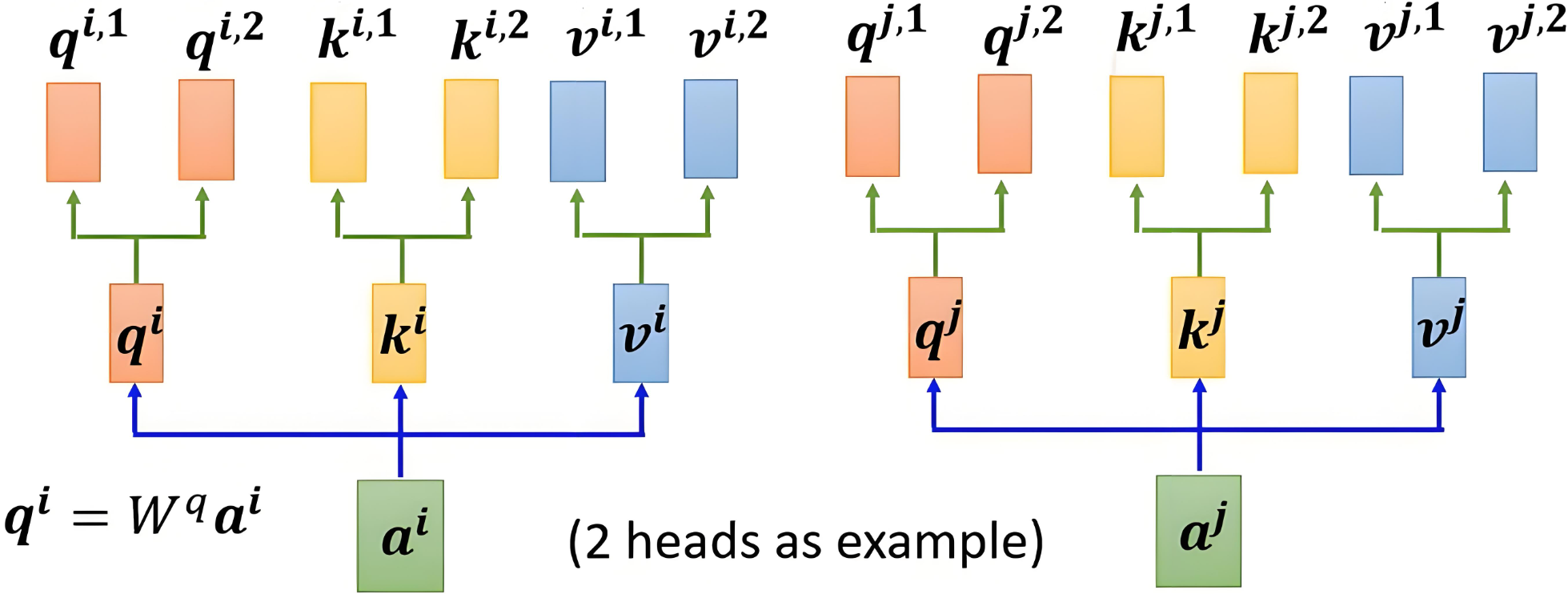
3.2 多頭機制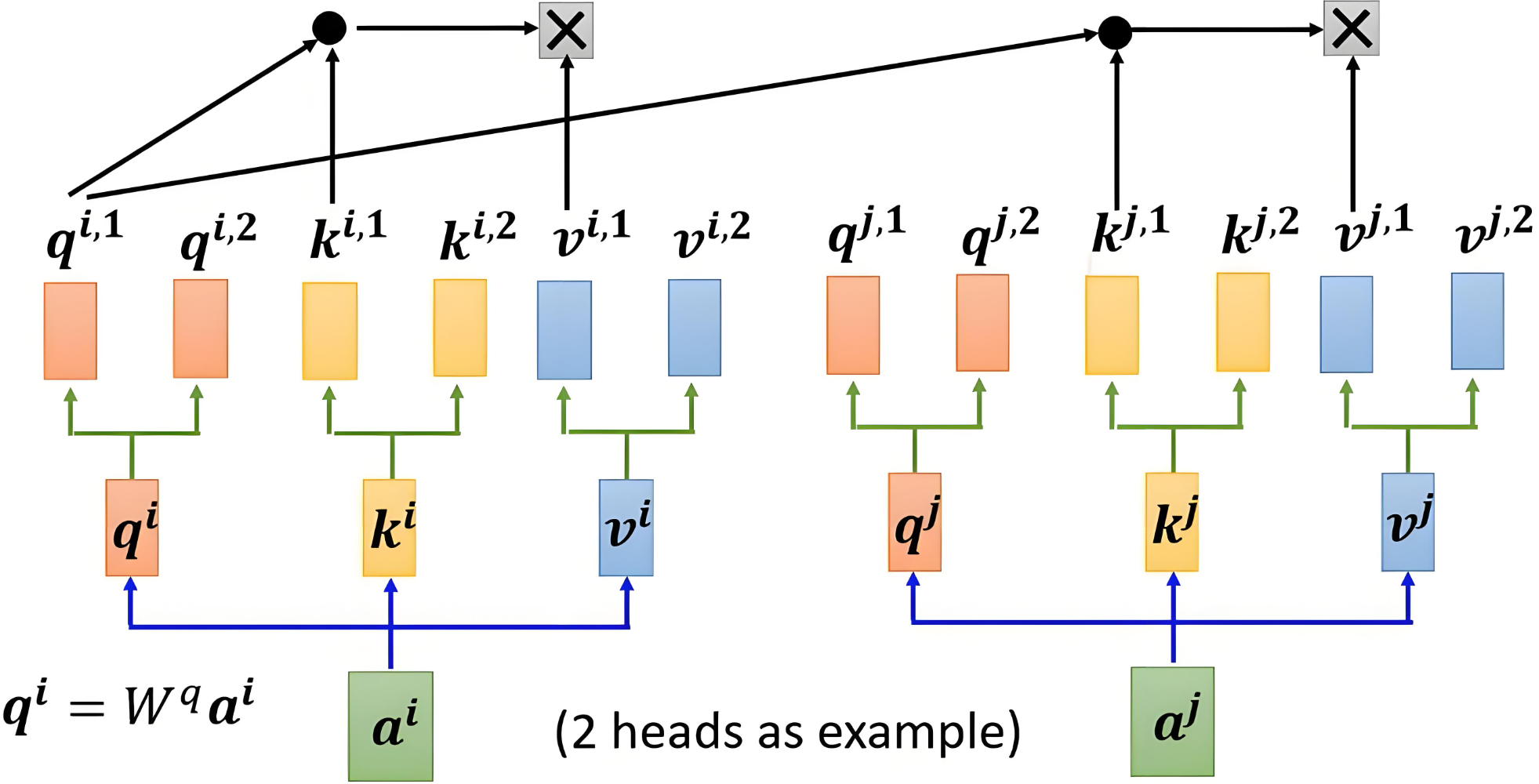

3.2.1 映射權重

分頭的過程是通過權重矩陣映射實現的，而不是直接切分

 head_num=8head_dim=dim // head_numfc=nn.ModuleList(nn.Linear(dim,dim) for _ in range(3))#映射QueryKeyValue矩陣Q=fc[0](sentence_embedding)K=fc[1](sentence_embedding)V=fc[2](sentence_embedding)#分成八個頭#每個映射創建出八個線性層multi_head_Q_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))multi_head_K_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))multi_head_V_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))#將不同的注意力頭進行映射然后堆疊起來multi_head_Q = torch.stack([multi_head_Q_fc[i](Q) for i in range(head_num)])print(multi_head_Q.shape)multi_head_K = torch.stack([multi_head_K_fc[i](K) for i in range(head_num)])print(multi_head_K.shape)multi_head_V = torch.stack([multi_head_V_fc[i](V) for i in range(head_num)])print(multi_head_V.shape)

3.3 加權求和

每個頭是獨立計算的，使用自己的一套參數，得到每個頭的輸出：
$$O_h=A_h{V}_h$$
其中，$O_h\in {\mathbb{R}}^{n\times d_v}$ 是第 $h$ 個頭的輸出。

  # 計算各自的注意力得分scores_list = torch.stack([torch.matmul(Query_list[i], Key_list[i].transpose(0, 1))for i in range(head_num)])scores_list = torch.stack([scores_list[i] / math.sqrt(d_k) for i in range(head_num)])# 進行歸一化操作scores_list = torch.stack([F.softmax(scores_list[i], dim=-1) for i in range(head_num)])print(scores_list)

3.4 輸出拼接

將所有頭的輸出進行拼接：
$$O_{\text{concat}}=[O_1,O_2,\dots ,O_h]\in {\mathbb{R}}^{n\times h?d_v}$$
其中，$O_{\text{concat}}$ 是所有頭拼接的結果，維度是 $n\times (h?d_v)$，其中 $h$ 是頭的數量，$d_v$ 是每個頭的值向量的維度。

# 對8個頭進行拼接，拼接形狀：(seq_len, d_k)Output = torch.cat(Output_list, dim=-1)print(Output.shape) # torch.Size([7, 512])

3.5 線性變換

拼接后通過一個線性變換矩陣 $W^O$ 映射為最終輸出：
$$\text{Output}=O_{\text{concat}}{W}^O$$
其中，$W^O\in {\mathbb{R}}^{(h?d_v)\times d}$ 是可訓練的權重矩陣，$d$ 是最終輸出的維度。

  # 線性變換并最終輸出W_O = torch.randn(dim, dim)Output = torch.matmul(Output, W_O)print(Output.shape) # torch.Size([7, 512])

3.3 表達能力

通過多個并行的頭在不同的子空間中學習上下文信息，讓同一個句子在不同場景下表達不同的意思，增強模型的表達能力和靈活性。