Pytorch深度學習框架實戰教程-番外篇05-Pytorch全連接層概念定義、工作原理和作用

?相關文章 + 視頻教程

《Pytorch深度學習框架實戰教程01》《視頻教程》

《Pytorch深度學習框架實戰教程02：開發環境部署》《視頻教程》

《Pytorch深度學習框架實戰教程03：Tensor 的創建、屬性、操作與轉換詳解》《視頻教程》

《Pytorch深度學習框架實戰教程04：Pytorch數據集和數據導入器》《視頻教程》

《Pytorch深度學習框架實戰教程05：Pytorch構建神經網絡模型》《視頻教程》

《Pytorch深度學習框架實戰教程06：Pytorch模型訓練和評估》《視頻教程》

《Pytorch深度學習框架實戰教程09：模型的保存和加載》《視頻教程》

《Pytorch深度學習框架實戰教程10：模型推理和測試》《視頻教程》

《Pytorch深度學習框架實戰教程-番外篇01-卷積神經網絡概念定義、工作原理和作用》

《Pytorch深度學習框架實戰教程-番外篇02-Pytorch池化層概念定義、工作原理和作用》

《Pytorch深度學習框架實戰教程-番外篇03-什么是激活函數，激活函數的作用和常用激活函數》

《PyTorch 深度學習框架實戰教程-番外篇04：卷積層詳解與實戰指南》

《Pytorch深度學習框架實戰教程-番外篇05-Pytorch全連接層概念定義、工作原理和作用》

《Pytorch深度學習框架實戰教程-番外篇06：Pytorch損失函數原理、類型和案例》

《Pytorch深度學習框架實戰教程-番外篇10-PyTorch中的nn.Linear詳解》

引言

你是否好奇，當神經網絡處理完圖像特征后，最終是如何判斷 "這是一只貓" 還是 "這是一只狗" 的？答案就藏在全連接層（Fully Connected Layer）里。作為神經網絡的 "決策中心"，全連接層承擔著特征整合與最終預測的關鍵角色。本文將帶你從底層原理到 PyTorch 實戰，徹底搞懂全連接層的工作機制。

一、什么是全連接層？

全連接層（又稱密集連接層，Dense Layer）是神經網絡中最基礎也最常用的層結構。其核心特征是：當前層的每個神經元與前一層的所有神經元完全連接，形成 "全連接" 的拓撲結構。

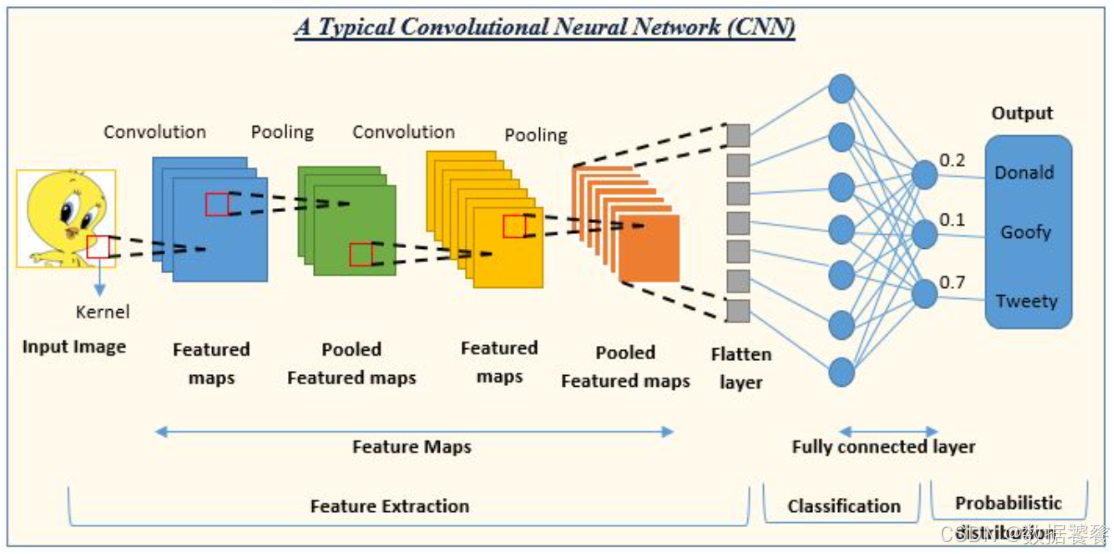
在 PyTorch 中，全連接層通過nn.Linear實現，它本質上是對輸入特征執行線性變換（矩陣乘法 + 偏置），并可配合激活函數實現非線性映射。

二、全連接層的工作原理：從數學到直觀理解

全連接層的工作過程可以拆解為兩個核心步驟，我們用具體例子說明：

1. 線性變換：矩陣乘法的魔力

假設前一層輸出的特征向量為x（形狀為[in_features]），全連接層的計算過程為：

y = x · W + b

其中：

W是權重矩陣（形狀為[out_features, in_features]），每個元素W[i][j]表示前層第j個神經元與當前層第i個神經元的連接強度；

b是偏置向量（形狀為[out_features]），為每個輸出神經元提供偏移量；

y是輸出向量（形狀為[out_features]），即線性變換的結果。

實例計算：

若輸入x = [x1, x2, x3]（in_features=3），輸出神經元數out_features=2，則：

y1 = x1×W11 + x2×W12 + x3×W13 + b1

y2 = x1×W21 + x2×W22 + x3×W23 + b2

用矩陣表即為：

[ y1 ] = [ W11 W12 W13 ] [x1] + [b1]

[ y2 ] [ W21 W22 W23 ] [x2] [b2]

[x3]

2. 非線性激活：突破線性限制

單純的線性變換無法擬合復雜數據分布（多層線性變換等價于單層線性變換），因此全連接層通常會搭配激活函數（如 ReLU、Sigmoid）：

y = σ(x · W + b)

激活函數為網絡引入非線性能力，使其能學習復雜的特征映射關系。例如在分類任務中，輸出層的全連接層會配合 Softmax 激活，將輸出轉換為類別概率分布。

三、全連接層的核心作用：從特征到決策

全連接層在神經網絡中扮演著 "決策者" 的角色，主要有三大作用：

1. 特征整合：將局部特征 "串聯" 成全局信息

在卷積神經網絡（CNN）中，卷積層和池化層提取的是局部特征（如邊緣、紋理、部件），而全連接層會將這些分散的局部特征整合為全局特征。例如：

卷積層可能檢測到 "貓的耳朵"" 貓的爪子 " 等局部特征；

全連接層則將這些特征整合，判斷 "這些特征組合起來是一只貓"。

2. 維度映射：將高維特征投影到目標空間

全連接層可以靈活調整特征維度，將前層輸出的高維特征映射到目標維度：

分類任務中，映射到[類別數]維度（如 10 類圖像分類輸出 10 維向量）；

回歸任務中，映射到[1]維度（如預測房價輸出單個數值）；

嵌入任務中，映射到指定維度的特征向量（如將文本映射到 128 維語義向量）。

3. 決策輸出：直接產生可解釋的預測結果

全連接層的輸出通常具有明確的業務含義：

分類問題中，輸出向量經過 Softmax 后表示每個類別的概率；

推薦系統中，輸出表示用戶對物品的偏好分數；

自動駕駛中，輸出表示轉向角度、剎車力度等控制信號。

四、PyTorch 全連接層實戰：從 API 到可視化

PyTorch 的nn.Linear是實現全連接層的核心 API，下面通過完整案例展示其用法。

1. nn.Linear核心參數解析

n.Linear(

in_features, # 輸入特征維度

out_features, # 輸出特征維度

bias=True # 是否添加偏置項（默認True）

)

參數數量計算：總參數量 = in_features × out_features + out_features（權重矩陣 + 偏置向量）；

輸入輸出形狀：輸入[batch_size, *, in_features] → 輸出[batch_size, *, out_features]（*表示任意中間維度）。

2. 完整實戰案例：MNIST 手寫數字識別中的全連接層

我們將構建一個含全連接層的神經網絡，用于 MNIST 手寫數字分類，并可視化全連接層的特征轉換過程。

import torchimport torch.nn as nnimport torchvision.datasets as datasetsimport torchvision.transforms as transformsimport matplotlib.pyplot as pltimport numpy as np# 1. 數據準備：加載MNIST數據集transform = transforms.Compose([transforms.ToTensor(), # 轉為Tensor（[1,28,28]）transforms.Normalize((0.1307,), (0.3081,)) # MNIST標準化參數])# 加載測試集（僅用于演示）test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=16, shuffle=True)# 2. 定義含全連接層的神經網絡class FCDemo(nn.Module):def __init__(self):super(FCDemo, self).__init__()# flatten：將28×28圖像展平為784維向量# 第一個全連接層：784→128（降維并提取特征）self.fc1 = nn.Linear(28*28, 128)# 第二個全連接層：128→64（進一步整合特征）self.fc2 = nn.Linear(128, 64)# 輸出層：64→10（10個數字類別）self.fc3 = nn.Linear(64, 10)# 激活函數self.relu = nn.ReLU()def forward(self, x, return_intermediate=False):# 展平圖像：[batch, 1, 28, 28] → [batch, 784]x = x.view(x.size(0), -1)# 記錄中間特征（用于可視化）x1 = self.relu(self.fc1(x)) # 第一個全連接層輸出x2 = self.relu(self.fc2(x1)) # 第二個全連接層輸出x3 = self.fc3(x2) # 輸出層if return_intermediate:return x3, x1, x2 # 返回輸出和中間特征return x3# 3. 初始化模型并加載預訓練權重（模擬訓練好的模型）model = FCDemo()# 為演示效果，隨機初始化一個"看起來合理"的權重def init_weights(m):if isinstance(m, nn.Linear):nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')if m.bias is not None:nn.init.constant_(m.bias, 0)model.apply(init_weights)# 4. 可視化全連接層的特征轉換過程def visualize_fc_transformations():# 獲取一批測試數據images, labels = next(iter(test_loader))# 前向傳播并獲取中間特征outputs, x1, x2 = model(images, return_intermediate=True)# 取第一個樣本進行可視化idx = 0img = images[idx].squeeze().numpy() # 原始圖像feat1 = x1[idx].detach().numpy() # 第一個全連接層輸出（128維）feat2 = x2[idx].detach().numpy() # 第二個全連接層輸出（64維）pred = torch.argmax(outputs[idx]).item() # 預測結果plt.figure(figsize=(15, 5))# 子圖1：原始圖像plt.subplot(1, 3, 1)plt.title(f"Original Image (Label: {labels[idx]}, Pred: {pred})")plt.imshow(img, cmap='gray')plt.axis('off')# 子圖2：第一個全連接層特征（128維）plt.subplot(1, 3, 2)plt.title("FC1 Output (128 features)")plt.bar(range(128), feat1)plt.xlabel("Feature Index")plt.ylabel("Activation Value")# 子圖3：第二個全連接層特征（64維）plt.subplot(1, 3, 3)plt.title("FC2 Output (64 features)")plt.bar(range(64), feat2)plt.xlabel("Feature Index")plt.ylabel("Activation Value")plt.tight_layout()plt.show()# 5. 打印模型參數信息def print_model_params():print("模型參數詳情：")for name, param in model.named_parameters():if 'weight' in name:print(f"{name}: 形狀 {param.shape}, 參數量 {param.numel()}")elif 'bias' in name:print(f"{name}: 形狀 {param.shape}, 參數量 {param.numel()}")total_params = sum(p.numel() for p in model.parameters())print(f"\n總參數量：{total_params}")# 執行可視化和參數打印if __name__ == "__main__":visualize_fc_transformations()print_model_params()