🍋🍋AI學習🍋🍋

🔥系列專欄： 👑哲學語錄: 用力所能及，改變世界。
💖如果覺得博主的文章還不錯的話，請點贊👍+收藏??+留言📝支持一下博主哦🤞

---

在神經網絡的訓練過程中，正向傳播和反向傳播是兩個關鍵步驟。在這兩個階段中，激活函數和損失函數扮演著不同的角色，并以特定的方式參與其中。下面我將詳細說明這兩個階段中激活函數和損失函數是如何工作的。

一、正向傳播（Forward Propagation）

1.?輸入層到隱藏層

• 輸入數據：首先，輸入數據 X 被傳遞給網絡的第一層。

• 線性變換：對于每一層 ll，輸入通過權重矩陣 W[l] 和偏置向量 b[l]進行線性變換。

• 應用激活函數：然后對 Z[l] 應用激活函數 g[l]，得到該層的激活輸出。

注意：這里激活函數輸出其實就是每個神經元傳遞給下一層的輸入。

2.?隱藏層到輸出層

• 最后一層：在輸出層，通常會使用一個特定的激活函數來適應任務的需求。例如：

  • 二分類問題：Sigmoid 激活函數，其輸出范圍為 (0, 1)，適合表示概率。
  • 多分類問題：Softmax 激活函數，用于將多個輸出值轉換為概率分布。
  • 回歸問題：可能不使用激活函數或使用線性激活函數。

• 計算預測值：最后一層的輸出 A[L] 就是我們模型的預測值 Y^。

3.?損失函數

• 計算損失：根據預測值?Y^?和真實標簽?Y，使用選定的損失函數?L(Y,Y^)L(Y,Y^)?來衡量模型的表現。常見的損失函數包括：
  • 均方誤差（MSE）：適用于回歸任務。
  • 交叉熵損失：適用于分類任務，特別是與 Sigmoid 或 Softmax 配合使用時。

二、反向傳播（Backward Propagation）

1.?從輸出層開始

• 起點梯度：反向傳播從計算輸出層的梯度開始。具體來說，我們首先需要計算損失函數對輸出層激活值的導數 ?L?A[L]?A[L]?L?。這個梯度被稱為“起點梯度”，因為它標志著梯度回傳過程的起始點。

  對于不同的損失函數，起點梯度的形式有所不同：

  • 均方誤差（MSE）+ 線性輸出：
  • 交叉熵 + Sigmoid/Softmax

2.?計算激活函數的導數

• 激活函數導數：接下來，我們需要計算激活函數的導數。這取決于使用的激活函數：

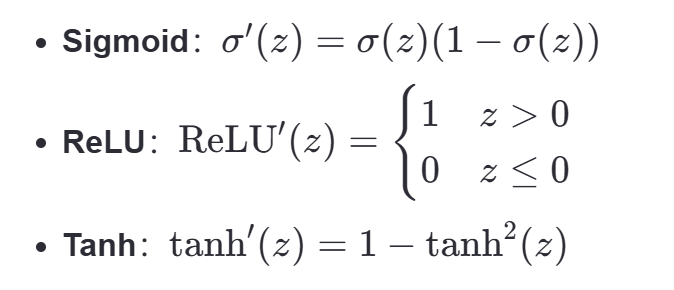
• 結合起點梯度，我們可以計算出損失相對于線性組合 Z[L] 的梯度

3.?逐層向前傳播梯度

• 正向傳播中的作用：

  • 激活函數：用于引入非線性，使得網絡能夠學習復雜的模式。每層的輸出都是前一層的激活輸出經過線性變換再通過激活函數的結果。
  • 損失函數：用于評估模型預測值與真實值之間的差距，提供了一個衡量模型性能的標準。

• 反向傳播中的作用：

  • 激活函數：其導數決定了梯度如何從當前層傳遞到前一層。不同激活函數的導數特性影響了梯度的傳播效率和穩定性。
  • 損失函數：提供了起點梯度，即損失相對于最后一層激活值的導數。這個初始梯度隨后通過鏈式法則逐層向前傳播，用于更新各層的參數。

三、總結：

在正向傳播過程中：

1.首先從輸入層到隱藏層經過線性變換得到輸出值Z，再將輸出值經過應用激活函數得到該層的的激活輸出A。

2.隱藏層到輸出層，在這里通常會使用一個他特定的激活函數來適應任務需求：

• 二分類問題：Sigmoid 激活函數，其輸出范圍為 (0, 1)，適合表示概率。

• 多分類問題：Softmax 激活函數，用于將多個輸出值轉換為概率分布。

• 回歸問題：可能不使用激活函數或使用線性激活函數。

最終計算得到最后一層的輸出，也就是我們的預測值。

3.損失函數L：我們開始計算損失根據模型的差異使用不一樣的損失函數（最后一層的輸出A就是預測值Y）

在反向傳播過程中：

1.首先計算損失函數對輸出層激活值的導數，這個梯度也就是起點梯度，標志著梯度回傳的起始點。

2.計算激活函數的導數A對Z求導，這里取決于使用的激活函數：Sigmoid、ReLU、Tanh等。

結合上起始點的梯度，我們可以計算出損失相對于線性組合 Z[L] 的梯度：

3.逐層向前傳播梯度